ビット演算を使用して Java で乗算を実装する方法

10 進数の乗算

たとえば、26 * 15 の乗算演算を実行する場合、通常は次のように計算します。まず、5 に 6 # を掛けます。 ##30 を取得し、0 を書き留めて 3 を脇に置き、5 に 2# を掛けます ##Get10 前の 3 を追加して 130 を取得するには、5 を計算した後、1 を計算します。 6 と 2 をそれぞれ計算し、その結果を以下の 26 に記録し、次に 130 と 26 を追加します (位置ずれあり) ) 結果は 390 になります。

2 進数の乗算

10 進数の乗算を読んだ後、2 進数の乗算を見てみましょう。基本原理は同じで、これも 2 進数で乗算されます。たとえば、

5 * 7

を計算します。

5

のバイナリ システムは 101、7 のバイナリ システムは 111 です。見てみましょう。バイナリクロス乗算法則。

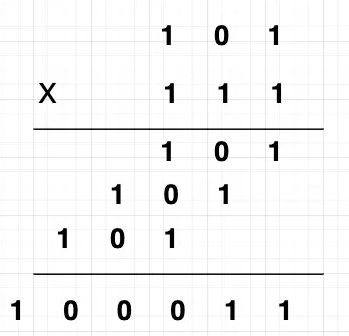2 進数

101

と 2 進数 111 が従来の方法で計算されていることがわかります。結果は 100011 で、バイナリ 100011 に対応する 10 進数は 35 です。 したがって、計算過程では、10 進数と 2 進数の計算方法は同じです。もちろん、ここでは例や証明は示しません。
アイデア分析

計算プロセスが完成したので、それをコードで実装するにはどうすればよいでしょうか?

上の図でバイナリ計算プロセスを見てみましょう:

最初にバイナリの最後の桁
• 111

  1 を使用します。 101 を掛けると 101 になります。

バイナリ
• 111

  の下から 2 番目の桁 1 を使用し、それに 101 を乗じて 101 を取得します。 ＃＃＃。

  2 進数
111

• 1 の下から 3 番目の桁を使用し、それに 101 を掛けて 101 を取得します。 ＃＃＃。 得られた 3 つの

  101
をバイナリ加算して、
• 100011

  を取得します。 ステップ

  2
と

3

で得られた結果 101 が 1 つ前に移動されていることに注意してください。 1010 と 10100、つまり、最終的な加算計算は 10100 1010 101 = 100011 となります。 最後の加算の計算を見てみましょう10100 1010 101 = 100011。つまり、データを複数の桁の加算に変換する方法が分かれば、次のとおりです。ビット単位の演算を使用して加算演算を実装する方法を学びます。

これら 3 つの数値 101、

1010

、10100 の数は、2 進数の 111## の数とまったく同じです。 #、つまり、2 進数の数 (上の図の下部にある乗数 111) を加算すると、いくつかの数値が生成されます。11111 を掛けると、 ##5数値が合計されます。 データの前に関係を見てみましょう: 最初の乗算結果:

101 = 101 0

• #2 回目の乗算の結果: 1111 = 101

• 3 回目の乗算の結果: 100011 = 101

• ここから、各計算で 101 を左に移動するだけでよいことがわかります。最後の計算結果を加算するだけです。

それでは、左に何回シフトするかをどうやって知ることができるのでしょうか?この例では、

111

は各計算後に右に 1 回移動し、101 も左に 1 回移動し、

111

の最後の桁だけが残ります。 . 、その後、計算を停止します。 コードの実装上記の考えに従って、コードを実装しましょう: <pre class="brush:java;">// 用位运算实现加法 public static int add(int a, int b) { int sum = 0; while (b != 0) { sum = a ^ b; b = (a &amp; b) &lt;&lt; 1; a = sum; } return sum; } // 用位运算实现减法 public static int multi(int a, int b) { int res = 0; while (b != 0) { if ((b &amp; 1) != 0) { res = add(res, a); } a &lt;&lt;= 1; b &gt;&gt;&gt;= 1; } return res; }</pre>コードを実行して結果を確認してください:

計算が正しく、負の数値もサポートされていることがわかります。

以上がビット演算を使用して Java で乗算を実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。