並列コンピューティングの定量的モデルと深層学習エンジンへの応用

UI。深層学習モデルをいかに迅速にトレーニングするかが業界の焦点となっており、業界関係者は特殊なハードウェアを開発したり、ソフトウェア フレームワークを開発したりして、それぞれ独自の能力を発揮しています。

もちろん、これらの法則は、この「コンピューター アーキテクチャ: 定量的アプローチ」などのコンピューター アーキテクチャの教科書や文献で見ることができますが、この記事の価値は、最も基本的な法則を的を絞った方法で選択することにあります。そしてそれらをディープラーニングエンジンと組み合わせて理解します。

1 計算量に関する前提条件

並列コンピューティングの定量的モデルを検討する前に、まずいくつかの設定を行います。特定の深層学習モデルの学習タスクでは、総計算量 V が一定であると仮定すると、V の大きさの計算が完了すれば深層学習モデルの学習は完了すると大まかに考えることができます。

この GitHub ページ (https://github.com/albanie/convnet-burden) には、一般的な CNN モデルが画像を処理するために必要な計算量がリストされています。フォワードフェーズの計算量は、トレーニングフェーズ中にバックワードフェーズの計算を必要とし、通常、バックワードフェーズの計算量がフォワード計算量よりも多くなる。この論文 (https://openreview.net/pdf?id=Bygq-H9eg) では、トレーニング段階での画像処理の計算量を直感的に視覚化した結果が得られます。

# ResNet-50 を例にとると、トレーニング フェーズでは 224X224x3 の画像を処理するために 8G-Ops (約 80 億回の計算) が必要です。ImageNet データ セット全体には約 120 万枚の画像があります。トレーニング プロセスでは、データ全体の 90 個の処理が必要です。エポック、概算、トレーニング プロセスには合計 (8*10^9) *(1.2*10^6)* 90 = 0.864*10^18 の演算が必要となり、ResNet-50 の合計計算量となります。トレーニング プロセスは約 10 億回の 10 億操作であるため、これらの計算が完了する限り、モデルの操作は完了すると単純に考えることができます。ディープ ラーニング コンピューティング エンジンの目標は、この指定された量の計算を最短時間で完了することです。

2 コンピューティング デバイスに関する前提条件

この記事は、下図に示すプロセッサ中心のコンピューティング デバイス (プロセッサ中心のコンピューティング) とメモリ中心のコンピューティング (メモリ内での処理) に限定されています。 ) デバイスは業界で検討されていますが、まだ主流ではありません。

上図に示すコンピューティング デバイスのコンピューティング ユニットは、CPU、GPGPU などの汎用プロセッサ、または TPU などの専用チップにすることができます。計算ユニットが汎用チップの場合、通常、プログラムとデータはメモリ ユニットに保存されます。メモリ ユニットは、現在最も人気のあるノイマン型コンピュータでもあります。

コンピューティング ユニットが専用チップである場合、通常はデータのみがメモリ ユニットに保存されます。通信ユニットは、記憶ユニットから演算ユニットへデータを転送し、データのロードを完了する役割を担い、演算ユニットがデータを取得した後、計算（データの形式変換）を完了する役割を担います。計算結果をメモリユニットに格納することでデータの保存（ストア）が完了します。

通信ユニットの送信能力は通常、メモリ アクセス帯域幅ベータ、つまり 1 秒あたりに転送できるバイト数で表されます。これは通常、ケーブルの数と周波数に関係します。シグナル。コンピューティング ユニットのコンピューティング能力は通常、1 秒あたりに完了できる浮動小数点計算 (フロップ) の数であるスループット レート pi で表されます。これは通常、コンピューティングに統合されている論理コンピューティング デバイスの数に関連します。単位とクロック周波数。

ディープ ラーニング エンジンの目標は、ソフトウェアとハ​​ードウェアの共同設計を通じてコン​​ピューティング デバイスのデータ処理能力を最大化すること、つまり、指定された量の計算を最短時間で完了することです。

3 ルーフライン モデル: 実際のコンピューティング パフォーマンスを表す数学的モデル

コンピューティング デバイスがタスクを実行するときに達成できる実際のコンピューティング パフォーマンス (1 秒あたりに完了する操作の数) は、単に関連しているだけではありません。メモリ アクセス帯域幅 Beta は、コンピューティング ユニットの理論上のピーク pi に関連し、また、現在のタスク自体の動作強度 (算術強度、または動作強度) にも関係します。

タスクの演算強度は、データの各バイトに必要な浮動小数点計算の数、つまりバイトあたりのフロップ数として定義されます。一般的に理解されているように、計算強度の低いタスクとは、通信ユニットによって転送されるバイトに対して計算ユニットが実行する操作が少なくて済むことを意味します。この場合、計算ユニットをビジー状態に保つために、通信ユニットは頻繁にデータを転送する必要があります。

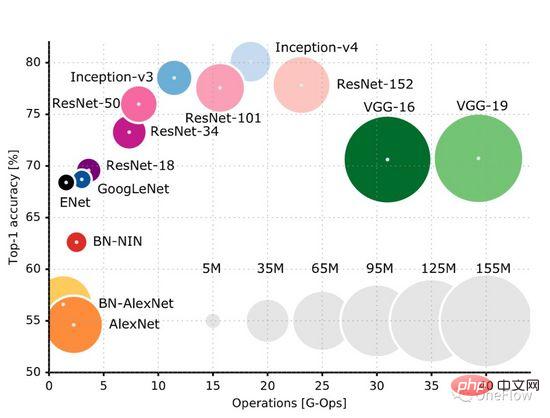
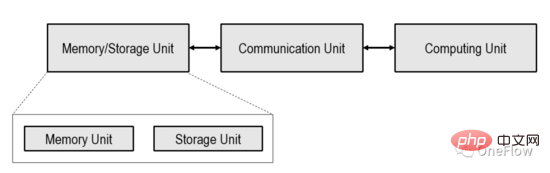
#計算強度の高いタスクとは、計算ユニットが通信ユニットによって転送されたバイトに対してより多くの操作を実行する必要があることを意味します。通信ユニットは、計算ユニットをビジー状態に保つためにそれほど頻繁にデータを転送する必要はありません。

まず第一に、実際の計算パフォーマンスは、計算ユニットの理論上のピーク pi を超えることはありません。第二に、メモリ アクセス帯域幅ベータが非常に小さい場合、1 秒でメモリから計算ユニットに転送できるのはベータ バイトだけです。現在の計算タスクの各バイトに必要な演算数を I とすると、ベータ * Iは 1 秒を表します。1 クロック内でデータを転送するために必要な実際の操作数です。beta * I

ルーフライン モデルは、メモリ アクセス帯域幅、コンピューティング ユニットのピーク スループット レート、およびタスクのコンピューティング強度の間の関係に基づいて実際のコンピューティング パフォーマンスを推測する数学的モデルです。 2008 年に David Patterson の Communication of ACM チームによって公開された ( https://en.wikipedia.org/wiki/Roofline_model )、これはシンプルでエレガントなビジュアル モデルです:

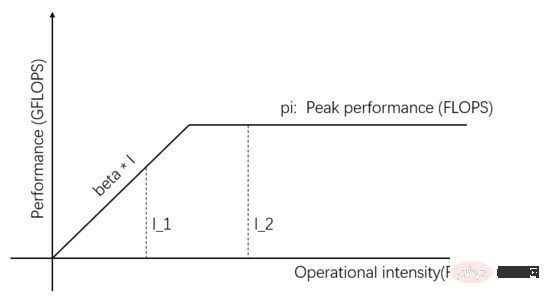
図 1: ルーフライン モデル

図 1 の横軸の独立変数は、さまざまなタスクの計算強度、つまりバイトごとに必要な浮動小数点演算の数を表します。縦軸の従属変数は、実際に達成可能な計算パフォーマンス、つまり 1 秒あたりに実行される浮動小数点演算の数を表します。上図は、演算強度 I_1 と I_2 の 2 つのタスクで実現できる実際の演算性能を示しています。I_1 の演算強度は pi/beta 未満であり、メモリアクセス制限タスクと呼ばれます。実際の演算性能 beta * I_1理論上のピーク pi よりも低いです。

I_2 の計算強度は pi/beta よりも高く、これは計算制限タスクと呼ばれます。実際の計算パフォーマンスは理論上のピーク pi に達し、メモリ アクセス帯域幅は pi/(I_2*beta のみを使用します) ）。図中の傾きの傾きをベータとします。その傾きと理論上のピークpi水平線との交点をリッジ点と呼びます。リッジ点の横軸はpi/ベータです。タスクの計算強度が等しい場合、 pi/beta、通信ユニット 演算ユニットとバランスが取れており、どちらも無駄がありません。

ディープ ラーニング エンジンの目標は「指定された量の計算を最短時間で完了する」ことであることを思い出してください。実際に達成可能なシステムのコンピューティング パフォーマンスを最大化する必要があります。この目標を達成するには、いくつかの戦略が利用可能です。図 1 の

I_2 はコンピューティングに制限されたタスクです。実際のコンピューティング パフォーマンスは、コンピューティング ユニットの並列性を高め、理論的なピーク値を増やすことで改善できます。たとえば、コンピューティング ユニットにさらに多くのコンピューティング ロジック ユニットを統合するなど、単位 (ALU)。ディープ ラーニング シナリオに特有の、1 つの GPU から同時に動作する複数の GPU まで GPU を追加することを意味します。

図 2 に示すように、計算ユニットに並列処理を追加すると、理論上のピーク値はベータ * I_2 よりも高くなり、実際の計算パフォーマンスは I_2 の方が高く、所要時間も短くなります。 。 できる。

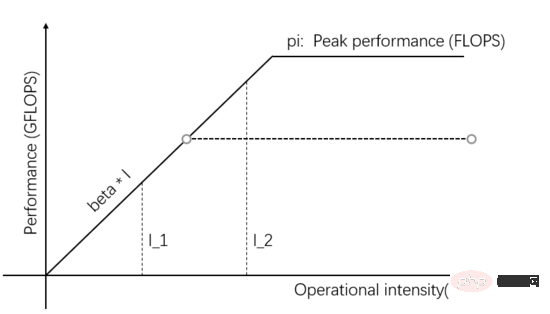
図 2: コンピューティング ユニットの理論上のピーク値を増やして実際のコンピューティング パフォーマンスを向上させる

図 1 の I_1 はメモリ アクセスが制限されたタスクです。通信ユニットの伝送帯域を向上させることで、実際の演算性能やデータ供給能力を向上させることができます。図3に示すように、傾きの傾きは通信ユニットの送信帯域幅を表しており、傾きの傾きが大きくなるとI_1はメモリアクセス制限タスクから演算制限タスクに変化し、実際の演算性能は改善されました。

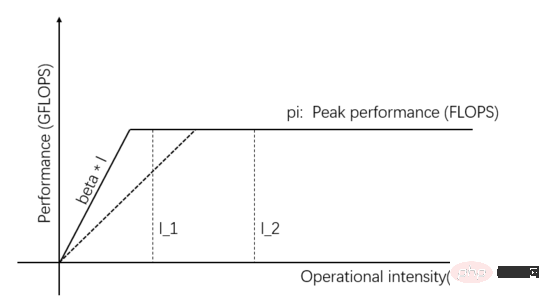
図 3: 通信ユニットのデータ供給能力を向上させ、実計算性能を向上

送信速度を向上させることで実計算性能を向上ハードウェアの帯域幅または理論上のピーク パフォーマンスに加えて、タスク自体の計算強度を向上させることによって、実際のコンピューティング パフォーマンスも向上させることができます。同じタスクをさまざまな方法で実装でき、実装が異なると計算強度も異なります。計算強度が I_1 から pi/beta を超えるように変換されると、計算が制限されたタスクとなり、実際の計算パフォーマンスは pi に達し、元の beta*I_1 を超えます。

実際の深層学習エンジンでは、上記の 3 つの方法 (並列性の向上、伝送帯域幅の向上、計算強度の高いアルゴリズムの使用) がすべて使用されます。

4 アムダールの法則: 高速化率の計算方法は?

図 2 の例では、計算ユニットの並列性を高めることで実際の計算パフォーマンスが向上していますが、タスクの実行時間はどの程度短縮できるでしょうか?これは加速比の問題、つまり効率が何倍にも上がるということです。

議論の便宜上、(1) 現在のタスクは計算的に制限されていると仮定し、計算強度、つまり I*beta>pi を表します。計算ユニットの計算単位を s 倍に増やした後の理論的な計算ピークは s * pi です。タスクの計算強度 I が十分に高いため、理論的なピーク値が s 倍に増加した後も、依然として計算的に制限される、つまり I*beta > s*pi; (2) パイプラインが使用されないと仮定すると、通信ユニットと計算ユニットは常に順番に実行されます (パイプラインの影響については後で詳しく説明します)。タスクの実行効率が何倍になったか計算してみましょう。

理論上のピーク値が pi である初期状況では、通信ユニットは 1 秒でベータ バイトのデータを転送し、計算ユニットは計算を完了するのに (I*beta)/pi 秒を必要とします。つまり、I*beta の計算が 1 (I*beta)/pi 秒以内に完了すれば、(I*beta) / (1 (I*beta)/pi) の計算が単位時間当たり完了できます。総計算量をVとすると、合計t1=V*(1(I*β)/pi)/(I*β)秒かかります。

並列処理を増やして理論上の計算ピークを s 倍に増やした後でも、通信ユニットはベータ バイトのデータを転送するのに 1 秒かかり、計算ユニットは (I*beta)/(s*pi) を必要とします。完了するまでの秒数。計算します。総計算量を V とすると、タスクが完了するまでに t2=V*(1 (I*beta)/(s*pi))/(I*beta) 秒かかります。

t1/t2 を計算して加速度比を取得します: 1/(pi/(pi I*beta) (I*beta)/(s*(pi I*beta))) この式は申し訳ありませんが、読者は、それを自分で推測するのは比較的簡単です。

理論上のピーク値が pi の場合、データ転送に 1 秒、計算に (I*β)/pi 秒かかりますので、計算時間の割合は (I*β)/(pi I* beta )、p がこの比率を表し、(I*beta)/(pi I*beta) に等しいものとします。

加速度比 t1/t2 に p を代入すると、加速度比は 1/(1-p p/s) として得られます。これが有名なアムダールの法則です (https://en.wikipedia.org) /wiki/アムダールの法則)。ここで、p は並列化できる元のタスクの割合を表し、s は並列化の倍数を表し、1/(1-p p/s) は得られる高速化を表します。

単純な数値を使用して計算しましょう。通信ユニットのデータ転送に 1 秒かかり、演算ユニットの計算に 9 秒かかると仮定すると、p=0.9 となります。計算ユニットの並列性を強化し、理論上のピーク値を 3 倍 (s=3) に増やした場合、計算ユニットは計算を完了するのに 3 秒しかかかりません。アムダールの法則を使用すると、加速率は 2.5 倍であり、加速率 2.5 は計算ユニットの並列処理の 3 倍未満であることがわかります。

コンピューティング ユニットの並列度を上げることの甘さを味わってきましたが、さらに並列度 s を増やすことで、より良い加速率を得ることができますか?できる。たとえば、s=9 の場合、5 倍の加速比が得られますが、並列処理の増加によるメリットがどんどん小さくなっていることがわかります。

sを無限に増やして高速化率を上げることはできますか?はい、しかし、コスト効率はますます低くなっていきます。s が無限大になる傾向がある場合 (つまり、コンピューティング ユニットの理論上のピーク値が無限大である場合)、p/s が 0 になる傾向があると想像してください。比率は 1/(1-p)=10 です。

システム内に並列化できない部分(通信ユニット)がある限り、加速率は1/(1-p)を超えることはできません。

上記の解析では演算強度 I が無限大であることを前提としており、演算器の並列性を高めると、加速度比 1/(1-p) の上限よりも実際の状況が悪化する可能性があります。通常、通信ユニットは送信帯域幅が減少するにつれて、p が小さくなり、1/(1-p) が大きくなります。

この結論は非常に悲観的です。たとえ通信オーバーヘッド (1-p) が 0.01 しかないとしても、並列ユニットの数が数万であっても、最大の高速化しか得られないことを意味します。 100回の。 pをできるだけ1に近づける、つまり1-pを0に近づけて加速度を向上させる方法はないでしょうか？特効薬は組み立てラインです。

5 パイプライン: 万能薬

アムダールの法則を導き出すとき、通信ユニットと計算ユニットが直列に動作すると仮定しました。通信ユニットは常に最初にデータを運び、計算ユニットは計算を行います。完了後、通信ユニットはデータを転送し、再度計算するように要求されます。

通信ユニットと演算ユニットは同時に動作し、データの転送と計算を同時に行うことができますか?演算器がデータを計算した後、すぐに次のデータの計算を開始できれば、p はほぼ 1 になります。並列度 s をいくら増やしても、直線加速率が得られます。直線的な高速化が得られる条件を調べてみましょう。

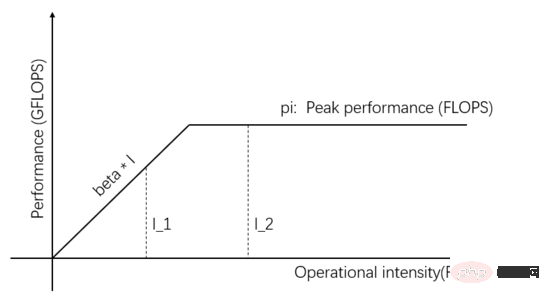
図 4: (図 1 と同じ) ルーフライン モデル

図 4 の I_1 は通信限定タスクであり、通信ユニットがそれを処理できます。ベータバイト データの場合、このベータバイトを処理するために演算ユニットが必要とする計算量は beta*I_1 演算です。理論上の計算ピークは pi で、合計 (beta*I_1)/pi 秒は次のようになります。計算を完了するために必要です。

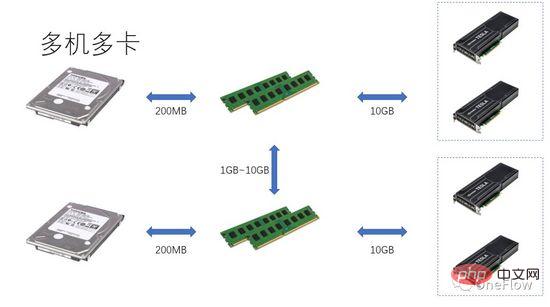
通信制限タスクの場合、beta*I_1

I_2 は、計算量が制限されたタスクです。通信ユニットは 1 秒でベータ バイトのデータを転送できます。これらのベータ バイトを処理するために計算ユニットが必要とする計算量は、beta*I_2 演算です。理論上計算 ピーク値は pi で、計算が完了するまでに (beta*I_2)/pi 秒かかります。コンピューティングが制限されたタスクの場合、beta*I_2>pi となるため、コンピューティング ユニットの計算時間は 1 秒を超えます。

これは、転送に 1 秒かかるデータの計算が完了するまでに数秒かかることも意味しており、計算時間、つまり計算時間内に次のデータを転送するのに十分な時間があります。データ転送時間の観点から言えば、p は最大 1 ですが、I が無限大である限り、加速率は無限大で構いません。

通信ユニットと計算ユニットをオーバーラップできるようにする技術はパイプラインと呼ばれます (パイプライン: https://en.wikipedia.org/wiki/Pipeline_(computing) )。これは、演算ユニットの使用率を効果的に向上させ、加速率を向上させるテクノロジーです。

6 ディープ ラーニング エンジンの並列コンピューティングの定量的モデルのインスピレーション

上で説明したさまざまな定量的モデルは、ディープ ラーニング エンジンの開発にも適用できます。たとえば、コンピューティングが限定されたタスクの場合、加速するために並列度を増やす (グラフィックス カードを増やす) ことができます。同じハードウェア デバイスが使用されている場合でも、異なる並列方式 (データ並列処理、モデル並列処理、またはパイプライン並列処理) を使用すると、計算強度 I に影響があり、実際の計算パフォーマンスに影響します。 ; 分散ディープラーニング エンジンには大量の通信オーバーヘッドとランタイム オーバーヘッドが含まれており、これらのオーバーヘッドをどのように削減またはマスクするかが高速化効果にとって重要です。

プロセッサ中心のコンピューティング デバイスの観点から GPU トレーニングに基づくディープ ラーニング モデルを理解することで、読者はより良い加速率を得るためにディープ ラーニング エンジンを設計する方法を考えることができます。

単一マシンと単一カードの場合、GPU の 100% 使用率は、データ転送と計算パイプラインを完了することによってのみ達成できます。実際のコンピューティング パフォーマンスは、最終的には基礎となる行列計算の効率、つまり cudnn の効率に依存します。理論的には、シングル カード シナリオでは、さまざまなディープ ラーニング フレームワーク間にパフォーマンスのギャップがあってはなりません。

同じマシン内に GPU を追加して高速化したい場合は、単一カードのシナリオと比較して、GPU とさまざまなタスク間のデータ転送の複雑さが増加します。セグメンテーション方法により、異なる計算強度 I が生成される場合があります (たとえば、畳み込み層はデータ並列処理に適しており、全結合層はモデル並列処理に適しています)。通信オーバーヘッドに加えて、実行時のスケジューリング オーバーヘッドも高速化に影響します。

マルチマシンおよびマルチカードのシナリオでは、GPU 間のデータ転送の複雑さはさらに増加し​​ます。ネットワークを介したマシン間のデータ転送の帯域幅は、通常、GPU よりも低くなります。 PCIe を介したマシン内のデータ転送の帯域幅、これは並列度が増加したことを意味しますが、データ転送帯域幅は減少しました、つまりルーフライン モデルの対角線の傾きが小さくなったことを意味します。データ並列処理に適した CNN は、通常、比較的高い計算強度 I を意味します。RNN/LSTM など、計算強度 I がはるかに小さいモデルもあります。これは、パイプラインでの通信オーバーヘッドがより困難であることも意味します。隠ぺいする。

7 要約

分散ディープラーニング エンジンを使用したことのある読者は、ソフトウェア フレームワークの加速率を個人的に経験しているはずです。基本的に、畳み込みニューラル ネットワークはデータの並列処理 (計算強度) に適しています。より高い I) を持つモデルの場合、GPU を追加することによる高速化の効果は非常に満足のいくものです。ただし、モデル並列処理を使用し、より高い計算強度を持つニューラル ネットワークのクラスが多数あります。また、モデル並列処理が使用されたとしても、計算量は強度はまだ非常に低く、畳み込みニューラル ネットワークよりもはるかに低いですが、GPU の並列処理を増やしてこれらのアプリケーションを高速化する方法は、業界の未解決の問題です。

以前の深層学習の評価では、複数の GPU を使用して RNN をトレーニングすると、単一の GPU よりも速度が低下することさえありました ( https://rare-technologies.com/machine-learning-hardware-benchmarks/ )。深層学習エンジンの効率の問題を解決するためにどのようなテクノロジーが使用されても、それは変わりません。加速率を改善するには、実行時のオーバーヘッドを削減し、適切な並列モードを選択して計算強度を高め、マスキングすることがすべてです。パイプラインを介した通信オーバーヘッド 本記事で説明する基本法がカバーする範囲内。

以上が並列コンピューティングの定量的モデルと深層学習エンジンへの応用の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。