連続順位付け確率スコア (CRPS) または「連続順位付け確率スコア」は、分布予測を真の値と比較する関数または統計です。

#機械学習ワークフローの重要な部分はモデルの評価です。プロセス自体は常識であると考えられます。データをトレーニング セットとテスト セットに分割し、トレーニング セットでモデルをトレーニングし、スコアリング関数を使用してテスト セットでのパフォーマンスを評価します。
スコアリング関数 (またはメトリック) は、真の値とその予測を単一の比較可能な値にマッピングします [1]。たとえば、継続的な予測の場合、RMSE、MAE、MAPE、R-squared などのスコアリング関数を使用できます。予測がポイントごとの推定ではなく、分布である場合はどうなるでしょうか?
ベイジアン機械学習では、予測は通常、点ごとの推定ではなく、値の分布です。たとえば、予測は分布の推定パラメーター、またはノンパラメトリックの場合は MCMC メソッドからのサンプルの配列にすることができます。
この場合、従来のスコアリング関数は統計設計には適していません。予測分布を平均値または中央値に集約すると、予測分布の分散と形状に関するかなりの情報が失われます。
CRPS
連続段階的確率スコア (CRPS) は、単一の真の値を累積分布関数 (CDF) と比較する分数関数です。
##これは 1970 年代に初めて導入され [4]、主に天気予報を目的としており、現在では文献や業界で再び注目を集めています [1] [6]。これは、ターゲット変数が連続であり、モデルがターゲットの分布を予測する場合に、モデルのパフォーマンスを評価するためのメトリクスとして使用できます。例には、ベイズ回帰またはベイズ時系列モデルが含まれます [5]。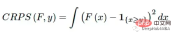 CRPS は、CDF を使用することでパラメトリック予測とノンパラメトリック予測の両方に役立ちます。多くの分布に対して、CRPS [3] には分析式があり、ノンパラメトリック予測に対しては、CRPS は経験的累積分布関数 (eCDF) を使用します。 )。
CRPS は、CDF を使用することでパラメトリック予測とノンパラメトリック予測の両方に役立ちます。多くの分布に対して、CRPS [3] には分析式があり、ノンパラメトリック予測に対しては、CRPS は経験的累積分布関数 (eCDF) を使用します。 )。
テスト セット内の各観測値の CRPS を計算した後、結果を 1 つの値に集計する必要もあります。 RMSE および MAE と同様に、これらは (おそらく加重された) 平均を使用して要約されます。
単一値を分布と比較する際の主な課題は、個々の値をどのように変換するかです。分布の表現。 CRPS は、指標関数を使用してグラウンド トゥルースを縮退分布に変換することで、この問題を解決します。たとえば、真の値が 7 の場合、次のように使用できます。
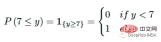
 CRPS は、有名な MAE (平均絶対誤差) と密接に関連しています。ポイントごとの予測を使用し、それを縮退 CDF として扱い、CRPS 方程式に注入すると、次の結果が得られます。
CRPS は、有名な MAE (平均絶対誤差) と密接に関連しています。ポイントごとの予測を使用し、それを縮退 CDF として扱い、CRPS 方程式に注入すると、次の結果が得られます。
 モデルの予測がパラメトリック分布である場合 (たとえば、分布パラメーターを予測する必要がある場合)、CRPS にはいくつかの一般的な分布に対する分析式があります [3]。モデルが正規分布のパラメーター μ と σ を予測する場合、CRPS は次の式を使用して計算できます。
モデルの予測がパラメトリック分布である場合 (たとえば、分布パラメーターを予測する必要がある場合)、CRPS にはいくつかの一般的な分布に対する分析式があります [3]。モデルが正規分布のパラメーター μ と σ を予測する場合、CRPS は次の式を使用して計算できます。
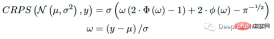 予測がノンパラメトリックである場合、つまり予測が一連のシミュレーションである場合、eCDF の計算は面倒な作業になります。ただし、CRPS は次のように表すこともできます:
予測がノンパラメトリックである場合、つまり予測が一連のシミュレーションである場合、eCDF の計算は面倒な作業になります。ただし、CRPS は次のように表すこともできます:
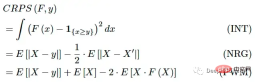
ここで、X、X' は F に独立しており、同一に分散されています。これらの式は計算が簡単ですが、それでもある程度の計算が必要です。
Python 実装
import numpy as np # Adapted to numpy from pyro.ops.stats.crps_empirical # Copyright (c) 2017-2019 Uber Technologies, Inc. # SPDX-License-Identifier: Apache-2.0 def crps(y_true, y_pred, sample_weight=None): num_samples = y_pred.shape[0] absolute_error = np.mean(np.abs(y_pred - y_true), axis=0) if num_samples == 1: return np.average(absolute_error, weights=sample_weight) y_pred = np.sort(y_pred, axis=0) diff = y_pred[1:] - y_pred[:-1] weight = np.arange(1, num_samples) * np.arange(num_samples - 1, 0, -1) weight = np.expand_dims(weight, -1) per_obs_crps = absolute_error - np.sum(diff * weight, axis=0) / num_samples**2 return np.average(per_obs_crps, weights=sample_weight)
CRPS 関数は NRG 形式 [2] に従って実装されます。 pyroppl[6]
import numpy as np def crps(y_true, y_pred, sample_weight=None): num_samples = y_pred.shape[0] absolute_error = np.mean(np.abs(y_pred - y_true), axis=0) if num_samples == 1: return np.average(absolute_error, weights=sample_weight) y_pred = np.sort(y_pred, axis=0) b0 = y_pred.mean(axis=0) b1_values = y_pred * np.arange(num_samples).reshape((num_samples, 1)) b1 = b1_values.mean(axis=0) / num_samples per_obs_crps = absolute_error + b0 - 2 * b1 return np.average(per_obs_crps, weights=sample_weight)
から引用 上記のコードは、PWM 形式 [2] に基づいて CRPS を実装しています。
概要
連続順位付け確率スコア (CRPS) は、単一の真の値をその予測分布と比較するスコアリング関数です。この特性により、モデルは通常、点ごとの推定ではなく分布予測を出力するベイジアン機械学習に関連します。これは、分布予測用のよく知られた MAE を一般化したものと見ることができます。
パラメトリック予測の分析式があり、ノンパラメトリック予測の簡単な計算を実行できます。 CRPS は、継続的な目標を持つベイジアン機械学習モデルのパフォーマンスを評価するための新しい標準手法となる可能性があります。
以上がCRPS: ベイジアン機械学習モデルのスコアリング関数の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
 10生成AIコーディング拡張機能とコードのコードを探る必要がありますApr 13, 2025 am 01:14 AM
10生成AIコーディング拡張機能とコードのコードを探る必要がありますApr 13, 2025 am 01:14 AMねえ、忍者をコーディング!その日はどのようなコーディング関連のタスクを計画していますか?このブログにさらに飛び込む前に、コーディング関連のすべての問題について考えてほしいです。 終わり? - &#8217を見てみましょう
 革新を調理する:人工知能がフードサービスを変革する方法Apr 12, 2025 pm 12:09 PM
革新を調理する:人工知能がフードサービスを変革する方法Apr 12, 2025 pm 12:09 PM食品の準備を強化するAI まだ初期の使用中ですが、AIシステムは食品の準備にますます使用されています。 AI駆動型のロボットは、ハンバーガーの製造、SAの組み立てなど、食品の準備タスクを自動化するためにキッチンで使用されています
 Pythonネームスペースと可変スコープに関する包括的なガイドApr 12, 2025 pm 12:00 PM
Pythonネームスペースと可変スコープに関する包括的なガイドApr 12, 2025 pm 12:00 PM導入 Python関数における変数の名前空間、スコープ、および動作を理解することは、効率的に記述し、ランタイムエラーや例外を回避するために重要です。この記事では、さまざまなASPを掘り下げます
 ビジョン言語モデル(VLM)の包括的なガイドApr 12, 2025 am 11:58 AM
ビジョン言語モデル(VLM)の包括的なガイドApr 12, 2025 am 11:58 AM導入 鮮やかな絵画や彫刻に囲まれたアートギャラリーを歩くことを想像してください。さて、各ピースに質問をして意味のある答えを得ることができたらどうでしょうか?あなたは尋ねるかもしれません、「あなたはどんな話を言っていますか?
 MediaTekは、Kompanio UltraとDimenity 9400でプレミアムラインナップをブーストしますApr 12, 2025 am 11:52 AM
MediaTekは、Kompanio UltraとDimenity 9400でプレミアムラインナップをブーストしますApr 12, 2025 am 11:52 AM製品のケイデンスを継続して、今月MediaTekは、新しいKompanio UltraやDimenity 9400を含む一連の発表を行いました。これらの製品は、スマートフォン用のチップを含むMediaTekのビジネスのより伝統的な部分を埋めます
 今週のAIで:Walmartがファッションのトレンドを設定する前に設定しますApr 12, 2025 am 11:51 AM
今週のAIで:Walmartがファッションのトレンドを設定する前に設定しますApr 12, 2025 am 11:51 AM#1 GoogleはAgent2Agentを起動しました 物語:月曜日の朝です。 AI駆動のリクルーターとして、あなたはより賢く、難しくありません。携帯電話の会社のダッシュボードにログインします。それはあなたに3つの重要な役割が調達され、吟味され、予定されていることを伝えます
 生成AIは精神障害に会いますApr 12, 2025 am 11:50 AM
生成AIは精神障害に会いますApr 12, 2025 am 11:50 AM私はあなたがそうであるに違いないと思います。 私たちは皆、精神障害がさまざまな心理学の用語を混ぜ合わせ、しばしば理解できないか完全に無意味であることが多い、さまざまなおしゃべりで構成されていることを知っているようです。 FOを吐き出すために必要なことはすべてです
 プロトタイプ:科学者は紙をプラスチックに変えますApr 12, 2025 am 11:49 AM
プロトタイプ:科学者は紙をプラスチックに変えますApr 12, 2025 am 11:49 AM今週公開された新しい研究によると、2022年に製造されたプラスチックの9.5%のみがリサイクル材料から作られていました。一方、プラスチックは埋め立て地や生態系に積み上げられ続けています。 しかし、助けが近づいています。エンジンのチーム


ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

MantisBT
Mantis は、製品の欠陥追跡を支援するために設計された、導入が簡単な Web ベースの欠陥追跡ツールです。 PHP、MySQL、Web サーバーが必要です。デモおよびホスティング サービスをチェックしてください。

メモ帳++7.3.1
使いやすく無料のコードエディター

MinGW - Minimalist GNU for Windows
このプロジェクトは osdn.net/projects/mingw に移行中です。引き続きそこでフォローしていただけます。 MinGW: GNU Compiler Collection (GCC) のネイティブ Windows ポートであり、ネイティブ Windows アプリケーションを構築するための自由に配布可能なインポート ライブラリとヘッダー ファイルであり、C99 機能をサポートする MSVC ランタイムの拡張機能が含まれています。すべての MinGW ソフトウェアは 64 ビット Windows プラットフォームで実行できます。

PhpStorm Mac バージョン
最新(2018.2.1)のプロフェッショナル向けPHP統合開発ツール

SublimeText3 中国語版
中国語版、とても使いやすい







