Java データ構造の単連結リストと OJ の質問

この記事では、java に関する関連知識を提供します。主に、単一リンク リストや OJ の質問など、データ構造に関する関連コンテンツを紹介します。一緒に見てみましょう。皆様のお役に立てれば幸いです。役に立ちます。

推奨学習: 「java ビデオ チュートリアル 」

1. リンク リストとは何ですか?

リンク リストは、物理的な記憶構造における不連続な記憶構造であり、データ要素の論理的順序は、リンク リスト内の参照リンク順序によって実現されます。

人気のポイントは、各要素がノードであり、ポインタ フィールドを使用して後続のノードを接続することです。最初のノードには先行ノードがなく、最後のノードには後続ノードがありません。

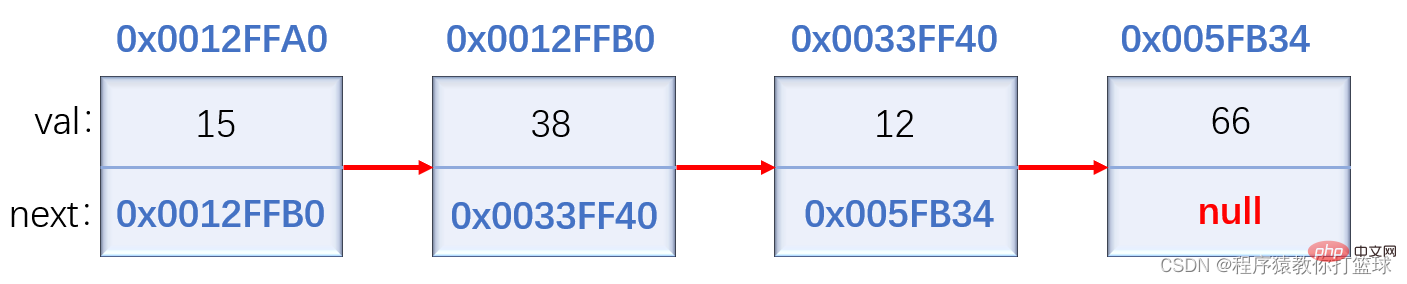
実際に実装されるリンクリストの構造は非常に多岐にわたり、以下の状況と組み合わせると8種類のリンクリスト構造になります。

1 . 一方向、双方向 2. 主導権を握るのではなく、主導権を握る 3. 周期的、非周期的

私たちは一方通行の説明に重点を置いています。非巡回リンクリストと双方向非巡回リンクリストがあり、この2つは筆記試験でも試験されます。

2. 一方向非巡回リンク リストの実装

2.1 実装前の合意

リンクされたリストはノードであるため、内部クラスのアプローチを採用し、常にヘッド ノードを指すようにヘッド ノードへの参照を定義する必要もあります。

public class MySingleList {
    private ListNode head; //引用头节点
    // 链表每个元素是一个节点
    private class ListNode {
        private int val; //存放数据元素
        private ListNode next; //存放下一个节点地址
        //构造方法
        public ListNode(int val) {
            this.val = val;
        }
    }
}

注: リンク リストには、データ フィールドとポインター フィールドという少なくとも 2 つのフィールドがあります。もちろん、複数のデータ フィールドとポインター フィールドを持つこともできます。

次の一般的に使用されるメソッドも実装する必要があります:

public void addFirst(int data); //头插法

public void addLast(int data); //尾插法

public boolean addIndex(int index,int data); //任意位置插入,第一个数据节点为0号下标

public boolean contains(int key); //查找关键字key是否在单链表当中

public void remove(int key); //删除第一次出现关键字为key的节点

public void removeAllKey(int key); //删除所有值为key的节点

public int size(); //得到单链表的长度

public void clear(); //清空链表

2.2 addFirst メソッド

public void addFirst(int data) {
    ListNode newNode = new ListNode(data); //把传过来的值放到新的节点中
    newNode.next = this.head; //新节点的next指向头节点
    this.head = newNode; //使新节点成为头节点
}

head はデフォルトで空を指しているため、リンクされたリストが null の場合、このコードの実行には影響しません。信じられない場合は、降りてきて絵を描いてください。

2.3 addList メソッド

public void addLast(int data) {
    ListNode newNode = new ListNode(data);
    // 如果链表为空的情况
    if (this.head == null) {
        this.head = newNode;
        return;
    }
    // 先找到最后一个节点
    ListNode cur = this.head;
    while (cur.next != null) {
        cur = cur.next;
    }
    cur.next = newNode;
}

2.4 addIndex メソッド

//任意位置插入,第一个数据节点为0号下标
private ListNode findIndexPrevNode(int index) {
    ListNode cur = this.head;
    while (index - 1 != 0) {
        cur = cur.next;
        index--;
    }
    return cur;
}
public boolean addIndex(int index,int data) {
    // 判断index下标的有效性
    if (index < 0 || index > size()) {
        return false;
    }
    // 如果在0下标插入则是头插
    if (index == 0) {
        addFirst(data); //头插
        return true;
    }
    // 如果在末尾插入则是尾插
    if (index == size()) {
        addLast(data); //尾插
        return true;
    }

    ListNode newNode = new ListNode(data); //新节点
    // 在中间插入
    ListNode prevNode = findIndexPrevNode(index); //找到index下标的前一个节点
    newNode.next = prevNode.next; //新节点的next被改为index的位置的节点
    prevNode.next = newNode; //index位置前一个节点next被改成新节点
    return true;
}

このコードでは、最初に前のノードを見つける必要があります。インデックス添字 , 最初に新しいノードをインデックス位置のノードにバインドし、次にインデックス位置にある前のノードを新しいノードに接続します。ここのテキストは明確ではありません。友人、あなたは降りてきて、次に従って絵を描くことができます私のコードを理解するには、C 言語でのデータ構造の実装に関するブロガーの図付きの以前のコラムを直接読むこともできます。

2.5 にはメソッドが含まれています

//查找关键字key是否在单链表当中
public boolean contains(int key) {
    // 当链表为空的情况
    if (this.head == null) {
        return false;
    }
    ListNode cur = this.head;
    // 遍历列表
    while (cur != null) {
        if (cur.val == key) {
            return true; //找到了返回true
        }
        cur = cur.next;
    }
    return false; //找不到返回false
}

アイデアは非常に単純で、リンクされたリストを走査して cur の空の位置を見つけます。true が返された場合、false が返されなかった場合、友達に任せて、降りてきて絵を描きましょう。

2.6 メソッドの削除

//删除第一次出现关键字为key的节点
public void remove(int key) {
    if (this.head == null) {
        return;
    }
    ListNode cur = this.head;

    // 如果删除的是key为头节点
    if (this.head.val == key) {
        this.head = head.next;
        return;
    }

    // 这里不能是cur!=null, 不然会越界！！！
    while (cur.next != null) {
        // 找到 key 的前一个节点
        if (cur.next.val == key) {
            //当前的cur为key的前一个节点
            cur.next = cur.next.next; //cur链接到key的后一个节点
            return;
        }
        cur = cur.next;
    }
}

ここでは、キーの前のノードを見つけて、それをキーの後ろのノードにバインドする必要があります。キーは使用できません。参照された場合、キーは自動的にリサイクルされます。

2.7 RemoveAllKey メソッド

//删除所有值为key的节点
public void removeAllKey(int key) {
    if (this.head == null) {
        return;
    }
    // 采用前后指针的方法
    ListNode cur = this.head;
    ListNode prev = this.head;
    while (cur != null) {
        if (cur.val == key) {
            prev.next = cur.next; //跳过key节点指向下一个节点
        } else {
            prev = cur;
        }
        cur = cur.next;
    }
    // 判断第一个节点是不是key
    if (this.head.val == key) {
        this.head = this.head.next; //head指向下一个节点
    }
}

まず、自分で見てみましょう。この質問については、後で OJ の質問を説明するときに詳しく説明します。

2.8 サイズと明確な方法

この 2 つの方法については、これ以上説明する必要はないと思います。トラバース？ヘッドポインタを直接nullに設定しますか?簡単ですよね？ここには書きません、任せます！

3. 単一リンク リスト OJ の質問の詳細な分析

これが今日のハイライトです。バスケットボール選手が絵を描かないわけではありません。前の絵は単純すぎるからです、友達。コードを組み合わせて自分で描くこともできますが、OJ の質問では、やはり絵を描く必要があります。これらの質問を読んだ後は、データ構造が好きになると思います。

3.1 リンクされたリスト要素を削除する (出典: LeetCode 難易度: 簡単)

質問:

あなたへリンク リスト head と整数 val の先頭ノード。Node.val == val を満たすリンク リスト内のすべてのノードを削除して # を返してください。 ## 新しいヘッド ノード 。

这个题我们可以用前后指针的思路来做，这样也比较通俗易懂，更适合初学者，大概的思路是这样的：我们可以定义一个cur和first的引用，如果碰到相等，也就是first.val == val，我们则让cur的next指向first的下一个节点，如果不相等，则让cur走到first的位置，最后first往后走一步，图解：

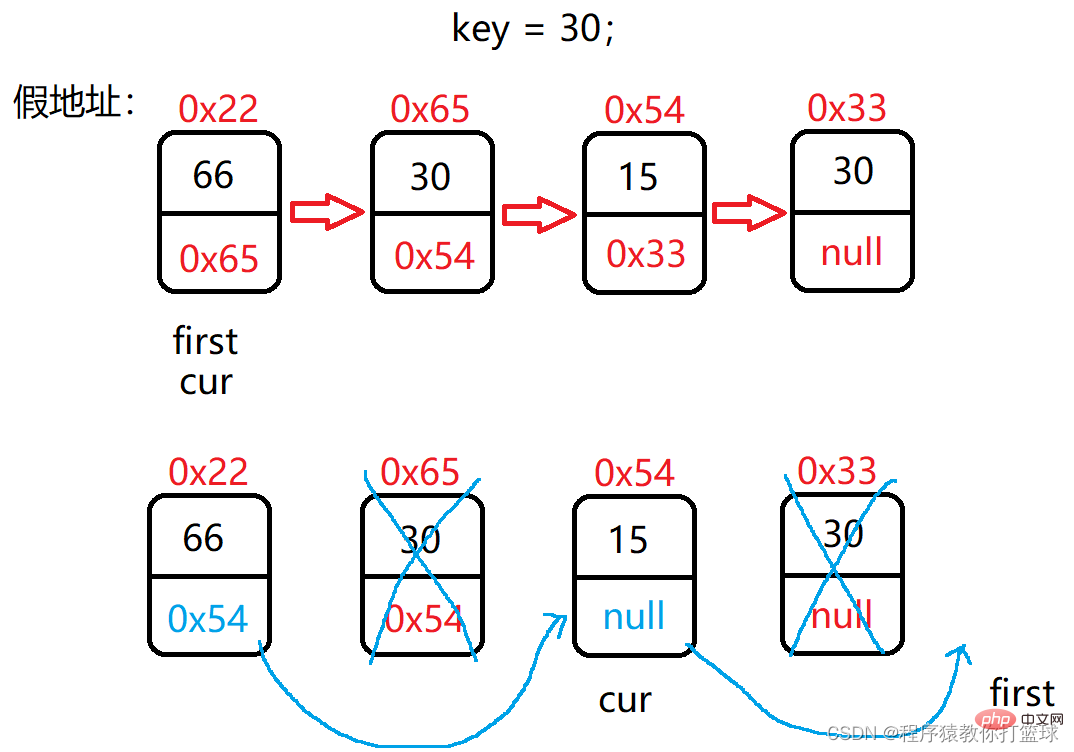
这里还没有完，如果第一个节点的值也是val呢？所以最后我们别忘了进行一个判断，那么最终的代码是这样的：

public ListNode removeElements(ListNode head, int val) {
    if (head == null) {
        return null;
    }
    ListNode cur = head;
    ListNode first = head;
    while (first != null) {
        if (first.val == val) {
            cur.next = first.next;
        } else {
            cur = first;
        }
        first = first.next;
    }
    // 判断头节点的值是否也是val
    if (head.val == val) {
        head = head.next;
    }
    return head;
}

3.2 反转链表(来源:LeetCode 难度:简单)

题目：给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。 

这个题我们可以先取到头节点，后续的节点都进行头插法即可？我们取到头节点，并且先将头节点的next置空，但是这样一来，就找不到后面的节点了，所以我们还需要有一个curNext引用来记录要反转节点的下一个节点：

我们的思路是这样的：首先找到头节点的next置空，cur走到curNext位置，curNext往前走，使得cur位置的next指向头节点，头节点cur再次成为新的头节点，当curNext走到null的时候循环结束。

public ListNode reverseList(ListNode head) {
    // 空链表的情况
    if (head == null) {
        return null;
    }
    ListNode cur = head;
    ListNode curNext = cur.next;
    head.next = null;
    while (curNext != null) {
        cur = curNext;
        curNext = curNext.next;
        cur.next = head;
        head = cur;
    }
    return head;
}

3.4 链表中倒数第k个节点

题目：输入一个链表，输出该链表中倒数第k个结点。 

这个题也是很简单的一道题，可以采用前后指针法，先让first指针走k步，走完之后slow和first一起走，这样slow和first之间就相差了k步，当first为null时，slow就是倒数第k个节点，在这个过程中，我们还要判断k的合法性，如果k小于等于0？或者k大于链表的长度呢？于是我们就能写出如下的代码：

public ListNode FindKthToTail(ListNode head,int k) {
    // 判断k的合法性
    if (k <= 0 || head == null) {
        return null;
    }
    ListNode first = head;
    ListNode slow = head;
    // 先让first走k步
    while (k != 0) {
        // k的长度大于链表的长度
        if (first == null) {
            return null;
        }
        first = first.next;
        k--;
    }
    // 一起走,当first为null,slow就是倒数第k个节点
    while (first != null) {
        first = first.next;
        slow = slow.next;
    }
    return slow;
}

3.6 链表分割(来源:牛客网 难度:较难) 

题目：现有一链表的头指针 ListNode* pHead，给一定值x，编写一段代码将所有小于x的结点排在其余结点之前，且不能改变原来的数据顺序，返回重新排列后的链表的头指针。 

这个题的思路我们可以这样做，既然是按照给定的值x进行分割，那么我们设定两个盘子，盘子A放小于x的节点，盘子B放大于x的节点，最后把这两个盘子的节点连起来，放回盘子A的头节点即可！

 public ListNode partition(ListNode pHead, int x) {
        if (pHead == null) {
            return null;
        }
        ListNode headA = null;
        ListNode headB = null;
        ListNode curA = null;
        ListNode curB = null;
        ListNode cur = pHead;
        while (cur != null) {
            if (cur.val < x) {
                // 第一次放入A盘子
                if (headA == null) {
                    headA = cur;
                    curA = cur;
                } else {
                    curA.next = cur;
                    curA = cur;
                }
            } else {
                // 第一次放入B盘子
                if (headB == null) {
                    headB = cur;
                    curB = cur;
                } else {
                    curB.next = cur;
                    curB = cur;
                }
            }
            cur = cur.next;
        }
        // 如果A盘子为空
        if (headA == null) {
            return headB;
        }
        curA.next = headB;
        // 避免B盘子尾节点形成环
        if (headB != null) {
            curB.next = null;
        }
        return headA;
    }

3.7 链表的回文结构(来源:LeetCode 难度:较难) 

题目：对于一个链表，请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法，判断其是否为回文结构。

给定一个链表的头指针A，请返回一个bool值，代表其是否为回文结构。保证链表长度小于等于900。

这个题有要求的，要求空间复杂度为O(1)，并且还得在O(n)的时间复杂度下，那我们就原地解决这个题，我们可以分为三个步骤，首先找到中间节点，然后把中间节点往后的节点进行反转，最后左右两个指针同时往中间走。如果光看下面代码看不懂，可以结合着代码画图才能理解更透彻哦！

public boolean chkPalindrome(ListNode A) {
    if (A == null) {
        return false;
    }
    // 只有一个节点的情况
    if (A.next == null) {
        return true;
    }
    // 首先找到中间节点
    ListNode first = A;
    ListNode slow = A;
    while (first != null && first.next != null) {
        first = first.next.next;
        slow = slow.next;
    }
    // 走到这,slow是链表的中间节点,采用头插法反转slow后续的节点
    first = slow.next;
    ListNode cur = slow;
    while (first != null) {
        cur = first;
        first = first.next;
        cur.next = slow; //链接前一个节点
        slow = cur; //更新头节点的位置
    }
    // 走到这,反转完毕,cur指向最后一个节点,让slow等于A,往中间找
    slow = A;
    while (slow != cur) {
        if (slow.val != cur.val) {
            return false;
        }
        // 偶数的情况下需要特殊判断
        if (slow.next == cur) {
            return true;
        }
        slow = slow.next;
        cur = cur.next;
    }
    return true;
}

3.8 相交链表(来源:LeetCode 难度:简单) 

题目：给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

这个题我们可以这样做，长链表先走两个链表的长度差的步数，因为相交之后的节点都是一样的个数，所以走了差值后，就两个链表一起往后走，相等了则就是相交节点。

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    if (headA == null || headB == null) {
        return null;
    }
    ListNode longList = headA; //longList始终记录长的链表
    ListNode shortList = headB;
    // 分别求出两个链表的长度
    int lenA = 0;
    int lenB = 0;
    ListNode cur = headA;
    while (cur != null) {
        lenA++;
        cur = cur.next;
    }
    cur = headB;
    while (cur != null) {
        lenB++;
        cur = cur.next;
    }
    int len = lenA - lenB;
    // 如果B链表长于A链表
    if (len < 0) {
        // 修正相差长度
        len = lenB - lenA;
        longList = headB; //longList始终记录长的链表
        shortList = headA;
    }
    // 让长链表先走差值len步,然后同步走,相等了即为相交节点
    while (len != 0) {
        longList = longList.next;
        len--;
    }
    while (longList != shortList) {
        longList = longList.next;
        shortList = shortList.next;
    }
    // 如果两个链表走到了null,则没有中间节点返回null,如果有,返回任意一个即可
    return longList;
}

推荐学习：《java视频教程》

以上がJava データ構造の単連結リストと OJ の質問の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。