JavaScript ツリー構造の深さ優先アルゴリズムを 1 つの記事でマスターする

この記事では、javascript に関する関連知識を提供し、主に JavaScript ツリー構造の深さ優先アルゴリズムを紹介します。ツリー構造は、フロントエンドで最も一般的なデータ構造の 1 つと言えます。たとえば、DOM ツリー、カスケード選択、ツリー コンポーネントについて見てみましょう。

[関連する推奨事項: JavaScript ビデオ チュートリアル 、Web フロントエンド ]

ツリーとは

実生活では、柳、ポプラ、桃など、木は誰もがよく知っていると思いますが、木は私たちの生活のどこにでもあると言えますが、コンピューターの世界では木は レイヤリングの一種 構造 、

の抽象モデルを次の図に示します。

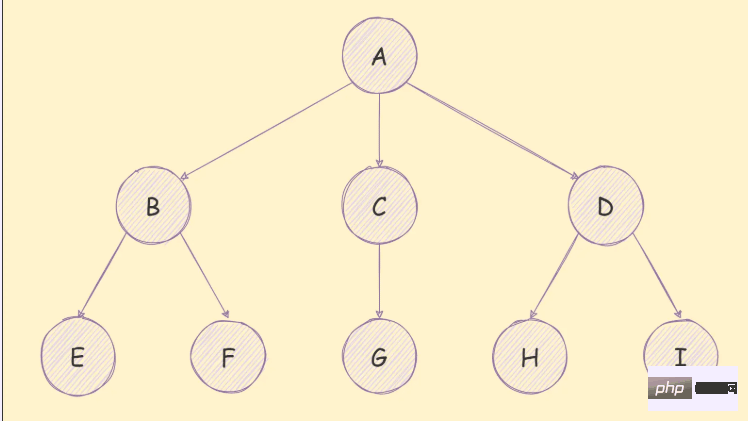
ツリー構造には多くの応用例があります。たとえば、以下に示すように、会社の組織構造をツリーで表すことができます。組織構造に加えて、家系図、州、都市などのツリー構造も使用して表現できます。

ツリーの用語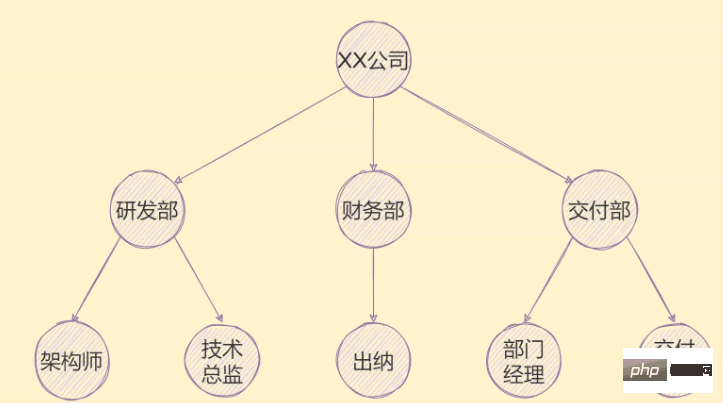

以下に示すように、ツリーには多くの用語があります。

Tree

: n (n≥0) 個のノードの有限セット。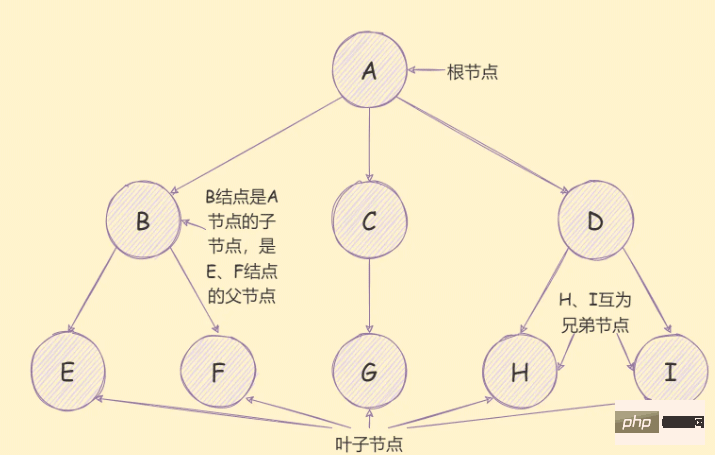n=0

の場合、それは空のツリーと呼ばれます。

• ノード : ノード の サブツリーの数、たとえば、ノード B の次数は 2、ノード A の次数は 3、
• 次数ツリー : ツリー全体 ノードの最大次数。たとえば、上の図では、ツリーの次数は 3;
リーフ ノード
• :次数 0 のノードはリーフ ノードとも呼ばれます;
• 子ノード: 上に示すように;
兄弟ノード
• :上図のように;
ルート ノード
• : 上図のように;
ツリーの深さ
• : 最大レベル 内のすべてのノードの間で、たとえば、上の図のツリーの深さは 3 です。
• ノードのレベル : たとえば、E のレベルノードは 3、ノードのレベルは 親ノードのレベルは 1、ルート ノードのレベルは 1;
• パス : あるノードから別のノードへのチャネル (たとえば、A→H のパスは
A D H
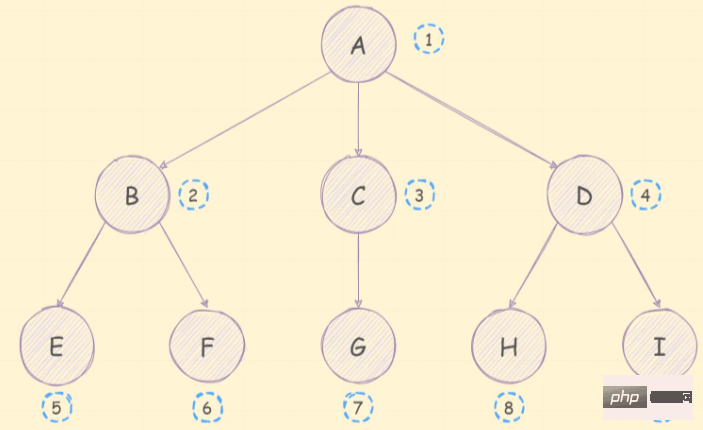
• ; パスの長さ : あるノードから別のノードまでの距離、たとえばパスA→Hは3です。
• JavaScript のツリーツリー構造は、DOM ツリー、カスケード選択、ツリー コンポーネント、 etc.;
JavaScript はツリー データ構造を提供しませんが、オブジェクトと配列を通じてツリーをシミュレートできます。

たとえば、次のコード:

const tree = {
  value: 'A',
  children: [
    {
      value: 'B',
      children: [
        { value: 'E', children: null },
        { value: 'F', children: null },
      ],
    },
    {
      value: 'C',
      children: [{ value: 'G', children: null }],
    },
    {
      value: 'D',
      children: [
        { value: 'H', children: null },
        { value: 'I', children: null },
      ],
    },
  ],
}

幅優先および深さ優先トラバーサル アルゴリズム

深さ優先

いわゆる深さ優先トラバーサル アルゴリズムは、ツリーのブランチを次のように検索します。その走査シーケンスは次のとおりです:

実装アイデアは次のとおりです:

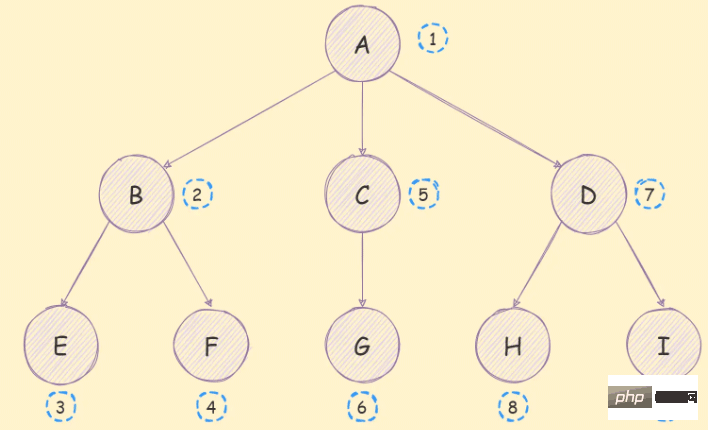#ルート ノードにアクセスします;

ルートへ ノードの children は深さ優先トラバーサル (再帰的) を実行し続けます;

• 実装コードは次のとおりです。
• <pre class="brush:js;">function dfs(root) { console.log(root.value) root.children &amp;&amp; root.children.forEach(dfs) // 与下面一致 // if (root.children) { // root.children.forEach(child =&gt; { // dfs(child) // }) // } } dfs(tree) // 这个tree就是前面定义的那个树 /* 结果 A B E F C G D H I */</pre>ご覧のとおり、図の順序は一貫しています。これは、アルゴリズムに問題がないことを意味します。

幅優先度

いわゆる幅優先度は、ルート ノードに最も近いノードを順番に訪問することです。その走査順序は次のとおりです:

実装のアイデアは次のとおりです:

キューを作成し、ルート ノードをキューに追加します。

キューの先頭をデキューしてアクセスします; キューの先頭にある

children

を順番にキューに追加します;
• ステップ 2 と 3 を繰り返します。キューは空です。
• 実装コードは次のとおりです。

function bfs(root) {
  // 1. 新建队列 跟节点入队
  const q = [root]
  // 4 重复执行
  while (q.length > 0) {
    const node = q.shift() // 2 队头出队
    console.log(node.value)
    // 3 队头 children 依次入队
    node.children &&
      node.children.forEach(child => {
        q.push(child)
      })
  }
}
bfs(tree)
/* 结果
A
B
C
D
E
F
G
H
I
*/

• ご覧のとおり、図の順序と一致しているため、問題はありません。私たちのアルゴリズムを使って。

【関連する推奨事項:

JavaScript ビデオ チュートリアル 、Web フロントエンド

]

以上がJavaScript ツリー構造の深さ優先アルゴリズムを 1 つの記事でマスターするの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。