ホームページ >ウェブフロントエンド >H5 チュートリアル >HTML5を使った3Dネットワークトポロジーツリーの実装(画像とテキストで詳しく解説)
HTML5を使った3Dネットワークトポロジーツリーの実装(画像とテキストで詳しく解説)
- 怪我咯オリジナル
- 2017-04-05 15:13:462686ブラウズ
HT for Web の 2D アプリケーションと 3D アプリケーションは両方とも、異なる表示効果を持つツリー構造データの表示をサポートしています。2D 上のツリー構造は明確な階層関係を表示しますが、データ量が多い場合、それほど直感的には見えません。 HT for Web のエラスティック レイアウト コンポーネントと組み合わせると、指定したノードを見つけるのがより困難になり、3D のツリー構造がより直感的に表示されます。ツリー構造データ全体の概要を一目で把握できます。伸縮性のある布 局の影響により、その階層構造はそれほど明確ではありません。このとき、明確な構造を持つ 3D ツリーが必要になります。それでは、この 3D ツリーがどのようなものなのか、一緒に見てみましょう~
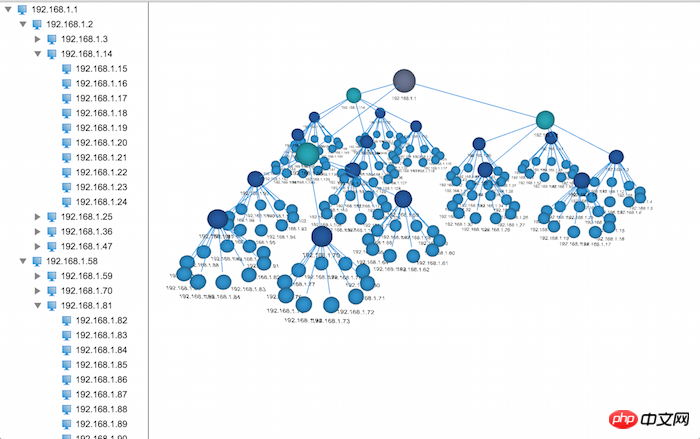
for ループ
をネストしてツリー構造のデータを作成します。ここでは詳しく説明しません。次に、2 番目の質問について説明します。2. 2D トポロジでの 3D ツリー構造の各層の半径計算をシミュレートします
3D でのツリー構造の最大の問題は、各ノードのレベルと、その親ノードの周囲のノードの各層の距離です。半径の計算。ツリー構造データが利用できるようになったので、2 層ツリー構造から半径の計算を開始します。
今度は 2 層ツリー構造を作成します。すべての子ノードが並んでいます。は親ノードを囲んでいないので、これらの子ノードの位置をどのように決定するのでしょうか?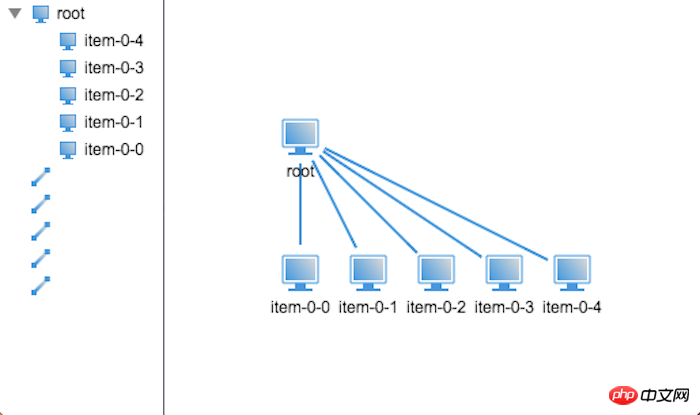 まず第一に、各エンドノードには独自のドメインの円があることを知る必要があります。そうでないと、ノード間で重複が生じます。そこで、ここでは、エンドノードのドメイン半径が 25 であると仮定し、その後 2 つのフェーズが隣接するノード間の最短距離はノード フィールド半径の 2 倍 (50) となり、これらの端ノードは親ノードを均等に取り囲みます。その後、2 つの隣接するノードの開口角度は、距離を使用して開口角度で確認できます。 2 点間の距離を求めると、親ノードの周囲のノードの最短半径を計算できます。開き角度を a、2 点間の最小距離を b とすると、最小半径 r の計算式は次のようになります。 = b / 2 / sin(a / 2);
まず第一に、各エンドノードには独自のドメインの円があることを知る必要があります。そうでないと、ノード間で重複が生じます。そこで、ここでは、エンドノードのドメイン半径が 25 であると仮定し、その後 2 つのフェーズが隣接するノード間の最短距離はノード フィールド半径の 2 倍 (50) となり、これらの端ノードは親ノードを均等に取り囲みます。その後、2 つの隣接するノードの開口角度は、距離を使用して開口角度で確認できます。 2 点間の距離を求めると、親ノードの周囲のノードの最短半径を計算できます。開き角度を a、2 点間の最小距離を b とすると、最小半径 r の計算式は次のようになります。 = b / 2 / sin(a / 2);
次に、ツリーをレイアウトしましょう。コードは次のように記述します。
/**
* 创建连线
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} source - 起点
* @param {ht.Node} target - 终点
*/
function createEdge(dataModel, source, target) {
// 创建连线,链接父亲节点及孩子节点
var edge = new ht.Edge();
edge.setSource(source);
edge.setTarget(target);
dataModel.add(edge);
}
/**
* 创建节点对象
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} [parent] - 父亲节点
* @returns {ht.Node} 节点对象
*/
function createNode(dataModel, parent) {
var node = new ht.Node();
if (parent) {
// 设置父亲节点
node.setParent(parent);
createEdge(dataModel, parent, node);
}
// 添加到数据容器中
dataModel.add(node);
return node;
}
/**
* 创建结构树
* @param {ht.DataModel} dataModel - 数据容器
* @param {ht.Node} parent - 父亲节点
* @param {Number} level - 深度
* @param {Array} count - 每层节点个数
* @param {function(ht.Node, Number, Number)} callback - 回调函数(节点对象,节点对应的层级,节点在层级中的编号)
*/
function createTreeNodes(dataModel, parent, level, count, callback) {
level--;
var num = (typeof count === 'number' ? count : count[level]);
while (num--) {
var node = createNode(dataModel, parent);
// 调用回调函数,用户可以在回调里面设置节点相关属性
callback(node, level, num);
if (level === 0) continue;
// 递归调用创建孩子节点
createTreeNodes(dataModel, node, level, count, callback);
}
}コードでは、デフォルトの終端半径が 25 に設定されていることがわかります。このように、layout() メソッドを呼び出して構造ツリーをレイアウトできます。レイアウト効果は次のとおりです。
レンダリングからわかるように、終了ノードのデフォルトの半径はあまり理想的ではありません。レイアウトの効果はほとんど目に見えないため、密すぎるレイアウトの問題を解決するために、エンド ノードのデフォルトの半径を増やすことができます。たとえば、デフォルトの半径を 40 に設定すると、次のような効果が得られます。现在两层的树状分布解决了,那么我们来看看三层的树状分布该如何处理。
将第二层和第三层看成一个整体,那么其实三层的树状结构跟两层是一样的,不同的是在处理第二层节点时,应该将其看做一个两层的树状结构来处理,那么像这种规律的处理用递归最好不过了,因此我们将代码稍微该着下,在看看效果如何:
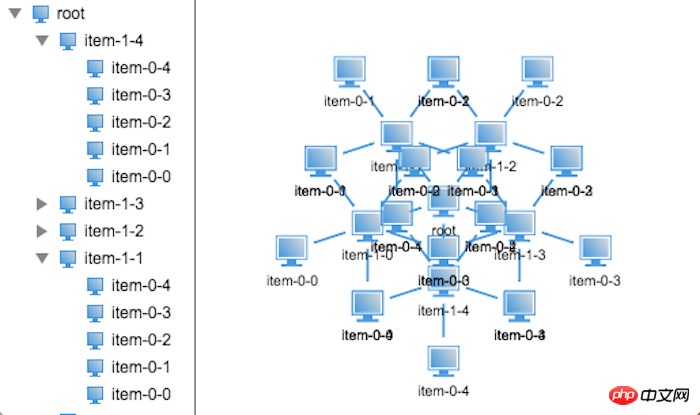
不行,节点都重叠在一起了,看来简单的递归是不行的,那么具体的问题出在哪里呢?
仔细分析了下,发现父亲节点的领域半径是由其孩子节点的领域半径决定的,因此在布局时需要知道自身节点的领域半径,而且节点的位置取决于父亲节点的领域半径及位置信息,这样一来就无法边计算半径边布局节点位置了。
那么现在只能将半径的计算和布局分开来,做两步操作了,我们先来分析下节点半径的计算:
首先需要明确最关键的条件,父亲节点的半径取决于其孩子节点的半径,这个条件告诉我们,只能从下往上计算节点半径,因此我们设计的递归函数必须是先递归后计算,废话不多说,我们来看下具体的代码实现:
/**
* 就按节点领域半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端节点,则设置其半径为最小半径
if (!root.hasChildren()) {
root.a('radius', minR);
return;
}
// 遍历孩子节点递归计算半径
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius');
// 计算子节点的1/2张角
var degree = Math.PI / children.size();
// 计算父亲节点的半径
var pRadius = radius / Math.sin(degree);
// 设置父亲节点的半径及其孩子节点的布局张角
root.a('radius', pRadius);
root.a('degree', degree * 2);
}OK,半径的计算解决了,那么接下来就该解决布局问题了,布局树状结构数据需要明确:孩子节点的坐标位置取决于其父亲节点的坐标位置,因此布局的递归方式和计算半径的递归方式不同,我们需要先布局父亲节点再递归布局孩子节点,具体看看代码吧:
/**
* 布局树
* @param {ht.Node} root - 根节点
*/
function layout(root) {
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = root.a('degree');
// 根据三角函数计算绕父亲节点的半径
var r = root.a('radius');
// 获取父亲节点的位置坐标
var rootPosition = root.p();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
y = c * r;
// 设置孩子节点的位置坐标
child.p(x + rootPosition.x, y + rootPosition.y);
// 递归调用布局孩子节点
layout(child);
});
}代码写完了,接下来就是见证奇迹的时刻了,我们来看看效果图吧:
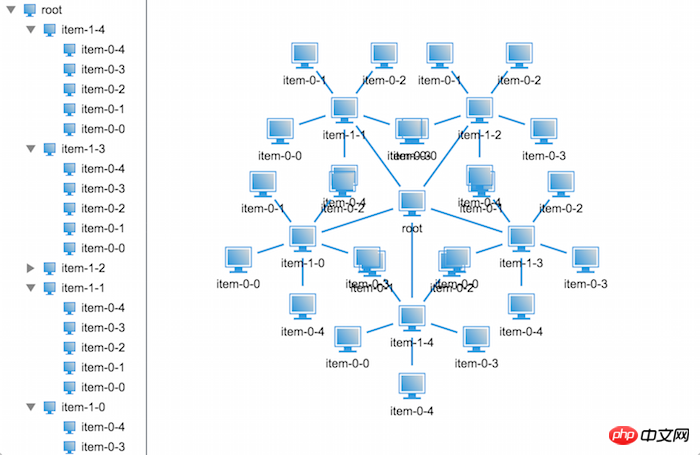
不对呀,代码应该是没问题的呀,为什么显示出来的效果还是会重叠呢?不过仔细观察我们可以发现相比上个版本的布局会好很多,至少这次只是末端节点重叠了,那么问题出在哪里呢?
不知道大家有没有发现,排除节点自身的大小,倒数第二层节点与节点之间的领域是相切的,那么也就是说节点的半径不仅和其孩子节点的半径有关,还与其孙子节点的半径有关,那我们把计算节点半径的方法改造下,将孙子节点的半径也考虑进去再看看效果如何,改造后的代码如下:
/**
* 就按节点领域半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
……
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius');
var child00 = child0.getChildAt(0);
// 半径加上孙子节点半径,避免节点重叠
if (child00) radius += child00.a('radius');
……
}下面就来看看效果吧~
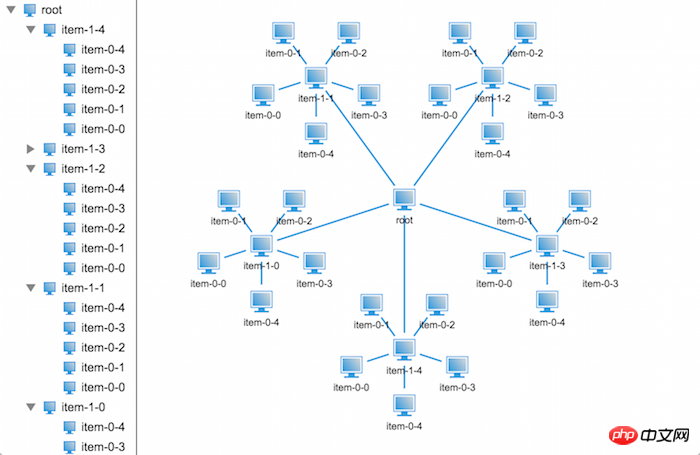
哈哈,看来我们分析对了,果然就不再重叠了,那我们来看看再多一层节点会是怎么样的壮观场景呢?
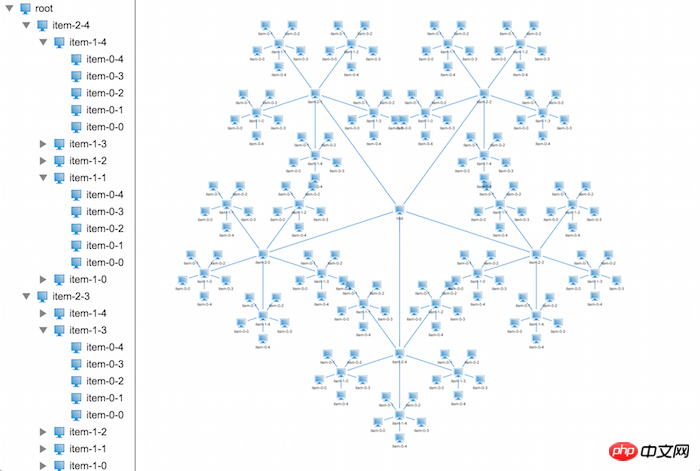
哦,NO!这不是我想看到的效果,又重叠了,好讨厌。
不要着急,我们再来仔细分析分析下,在前面,我们提到过一个名词——领域半径,什么是领域半径呢?很简单,就是可以容纳下自身及其所有孩子节点的最小半径,那么问题就来了,末端节点的领域半径为我们指定的最小半径,那么倒数第二层的领域半径是多少呢?并不是我们前面计算出来的半径,而应该加上末端节点自身的领域半径,因为它们之间存在着包含关系,子节点的领域必须包含于其父亲节点的领域中,那我们在看看上图,是不是感觉末端节点的领域被侵占了。那么我们前面计算出来的半径代表着什么呢?前面计算出来的半径其实代表着孩子节点的布局半径,在布局的时候是通过该半径来布局的。
OK,那我们来总结下,节点的领域半径是其下每层节点的布局半径之和,而布局半径需要根据其孩子节点个数及其领域半径共同决定。
好了,我们现在知道问题的所在了,那么我们的代码该如何去实现呢?接着往下看:
/**
* 就按节点领域半径及布局半径
* @param {ht.Node} root - 根节点对象
* @param {Number} minR - 最小半径
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端节点,则设置其布局半径及领域半径为最小半径
if (!root.hasChildren()) {
root.a('radius', minR);
root.a('totalRadius', minR);
return;
}
// 遍历孩子节点递归计算半径
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 获取孩子节点半径
var radius = child0.a('radius'),
totalRadius = child0.a('totalRadius');
// 计算子节点的1/2张角
var degree = Math.PI / children.size();
// 计算父亲节点的布局半径
var pRadius = totalRadius / Math.sin(degree);
// 缓存父亲节点的布局半径
root.a('radius', pRadius);
// 缓存父亲节点的领域半径
root.a('totalRadius', pRadius + totalRadius);
// 缓存其孩子节点的布局张角
root.a('degree', degree * 2);
}在代码中我们将节点的领域半径缓存起来,从下往上一层一层地叠加上去。接下来我们一起验证其正确性:
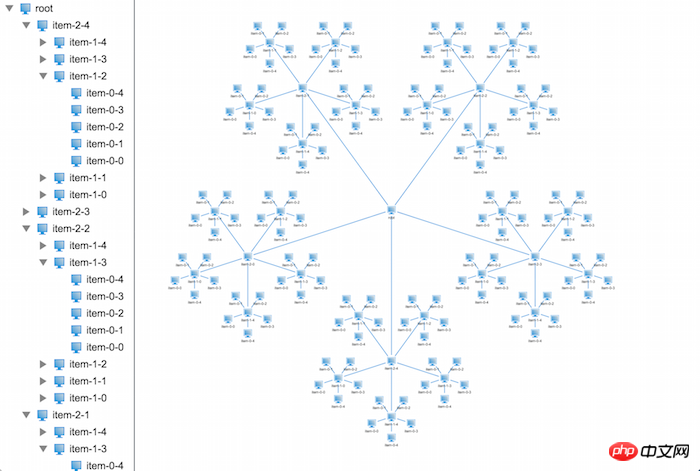
搞定,就是这样子了,2D拓扑上面的布局搞定了,那么接下来该出动3D拓扑啦~
3. 加入z轴坐标,呈现3D下的树状结构
3D拓扑上面布局无非就是多加了一个坐标系,而且这个坐标系只是控制节点的高度而已,并不会影响到节点之间的重叠,所以接下来我们来改造下我们的程序,让其能够在3D上正常布局。
也不需要太大的改造,我们只需要修改下布局器并且将2D拓扑组件改成3D拓扑组件就可以了。
/**
* 布局树
* @param {ht.Node} root - 根节点
*/
function layout(root) {
// 获取到所有的孩子节点对象数组
var children = root.getChildren().toArray();
// 获取孩子节点个数
var len = children.length;
// 计算张角
var degree = root.a('degree');
// 根据三角函数计算绕父亲节点的半径
var r = root.a('radius');
// 获取父亲节点的位置坐标
var rootPosition = root.p3();
children.forEach(function(child, index) {
// 根据三角函数计算每个节点相对于父亲节点的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
z = c * r;
// 设置孩子节点的位置坐标
child.p3(x + rootPosition[0], rootPosition[1] - 100, z + rootPosition[2]);
// 递归调用布局孩子节点
layout(child);
});
}上面是改造成3D布局后的布局器代码,你会发现和2D的布局器代码就差一个坐标系的的计算,其他的都一样,看下在3D上布局的效果:
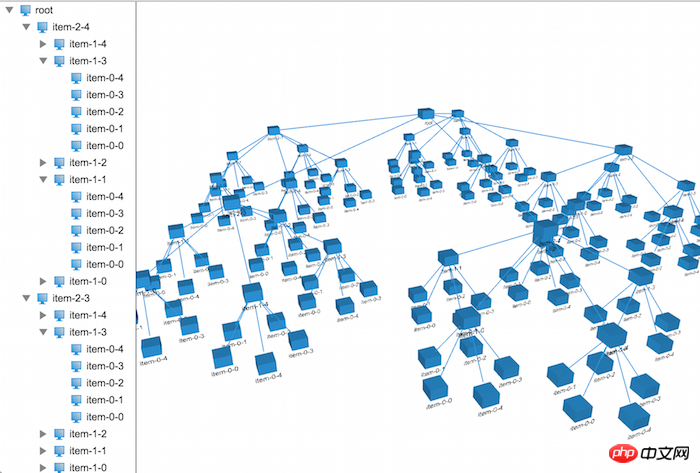
恩,有模有样的了,在文章的开头,我们可以看到每一层的节点都有不同的颜色及大小,这些都是比较简单,在这里我就不做深入的讲解,具体的代码实现如下:
var level = 4,
size = (level + 1) * 20;
var root = createNode(dataModel);
root.setName('root');
root.p(100, 100);
root.s('shape3d', 'sphere');
root.s('shape3d.color', randomColor());
root.s3(size, size, size);
var colors = {},
sizes = {};
createTreeNodes(dataModel, root, level - 1, 5, function(data, level, num) {
if (!colors[level]) {
colors[level] = randomColor();
sizes[level] = (level + 1) * 20;
}
size = sizes[level];
data.setName('item-' + level + '-' + num);
// 设置节点形状为球形
data.s('shape3d', 'sphere');
data.s('shape3d.color', colors[level]);
data.s3(size, size, size);
});在这里引入了一个随机生成颜色值的方法,对每一层随机生成一种颜色,并将节点的形状改成了球形,让页面看起来美观些(其实很丑)。
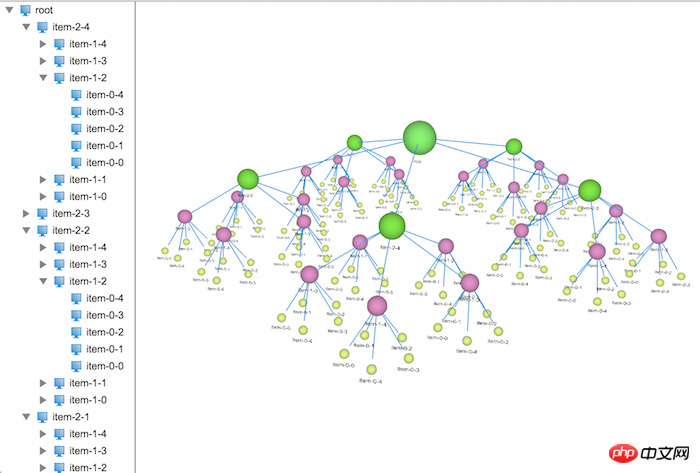
提个外话,节点上可以贴上图片,还可以设置文字的朝向,可以根据用户的视角动态调整位置,等等一系列的拓展,这些大家都可以去尝试,相信都可以做出一个很漂亮的3D树出来。
到此,整个Demo的制作就结束了,今天的篇幅有些长,感谢大家的耐心阅读,在设计上或则是表达上有什么建议或意见欢迎大家提出
以上がHTML5を使った3Dネットワークトポロジーツリーの実装(画像とテキストで詳しく解説)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

