Maison >Périphériques technologiques >IA >Nouveau mécanisme d'attention approximative HyperAttention : adapté aux contextes longs, accélérant l'inférence LLM de 50 %
Nouveau mécanisme d'attention approximative HyperAttention : adapté aux contextes longs, accélérant l'inférence LLM de 50 %
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-11-13 20:29:09961parcourir
Transformer a réussi une variété de tâches d'apprentissage dans des domaines tels que le traitement du langage naturel, la vision par ordinateur et la prédiction de séries chronologiques. Malgré leur succès, ces modèles sont encore confrontés à de sévères limitations d’évolutivité. La raison en est que le calcul exact de la couche d’attention entraîne un temps d’exécution quadratique (en longueur de séquence) et une complexité de mémoire. Cela pose des défis fondamentaux pour étendre le modèle Transformer à des longueurs de contexte plus longues
L'industrie a exploré diverses méthodes pour résoudre le problème des couches d'attention temporelle quadratiques, l'une des directions remarquables est l'attention approximative Matrice intermédiaire dans la couche de force. Les méthodes pour y parvenir incluent l'approximation via des matrices clairsemées, des matrices de bas rang ou une combinaison des deux.
Cependant, ces méthodes ne fournissent pas de garanties de bout en bout pour l'approximation de la matrice de sortie d'attention. Ces méthodes visent à approximer les composantes individuelles de l’attention plus rapidement, mais aucune ne fournit une approximation de bout en bout de l’attention complète du produit scalaire. Ces méthodes ne prennent pas non plus en charge l’utilisation de masques causals, qui constituent une partie importante des architectures Transformer modernes. Des limites théoriques récentes indiquent qu'en général, il n'est pas possible d'effectuer une approximation terminologique de la matrice d'attention en temps sous-quadratique
Cependant, une étude récente appelée KDEFormer montre que lorsque les termes de la matrice d'attention sont limités Sous les hypothèses de , il peut fournir des approximations prouvables en temps subquadratique. Théoriquement, le temps d'exécution de KDEFormer est d'environ 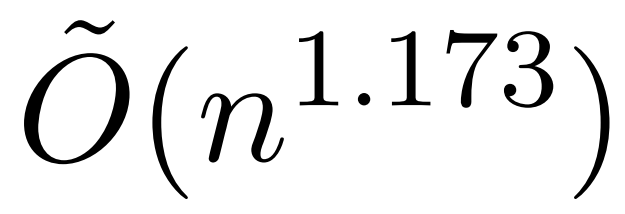 ; il utilise l'estimation de la densité du noyau (KDE) pour se rapprocher de la norme de colonne, permettant le calcul de la probabilité d'échantillonnage des colonnes de la matrice d'attention. Cependant, les algorithmes KDE actuels manquent d'efficacité pratique, et même en théorie, il existe un écart entre le temps d'exécution de KDEFormer et un algorithme de temps O(n) théoriquement réalisable. Dans l'article, l'auteur prouve que sous la même hypothèse d'entrée bornée, un algorithme de temps
; il utilise l'estimation de la densité du noyau (KDE) pour se rapprocher de la norme de colonne, permettant le calcul de la probabilité d'échantillonnage des colonnes de la matrice d'attention. Cependant, les algorithmes KDE actuels manquent d'efficacité pratique, et même en théorie, il existe un écart entre le temps d'exécution de KDEFormer et un algorithme de temps O(n) théoriquement réalisable. Dans l'article, l'auteur prouve que sous la même hypothèse d'entrée bornée, un algorithme de temps 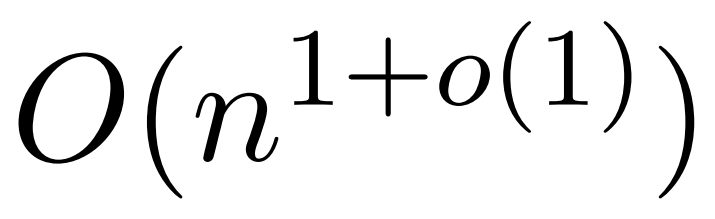 quasi linéaire est possible. Cependant, leur algorithme implique également l’utilisation de méthodes polynomiales pour se rapprocher du softmax, ce qui risque d’être peu pratique.
quasi linéaire est possible. Cependant, leur algorithme implique également l’utilisation de méthodes polynomiales pour se rapprocher du softmax, ce qui risque d’être peu pratique.
Dans cet article, des chercheurs de l'Université de Yale, de Google Research et d'autres institutions proposent un algorithme qui offre le meilleur des deux mondes, à la fois pratique et efficace, et peut obtenir la meilleure garantie de temps quasi-linéaire. De plus, la méthode prend en charge le masquage causal, ce qui n’était pas possible dans les travaux antérieurs.

Veuillez cliquer sur le lien suivant pour consulter l'article : https://arxiv.org/abs/2310.05869
Cet article propose un mécanisme d'attention approximative appelé "HyperAttention" conçu pour relever les défis informatiques. posé par l’utilisation de contextes longs dans de grands modèles de langage. Des recherches récentes montrent que dans le pire des cas, à moins que les entrées de la matrice d'attention ne soient bornées ou que le rang stable de la matrice soit faible, un temps quadratique est nécessaire
Réécrit comme suit : Les chercheurs ont introduit deux paramètres à mesurer : (1) la norme de colonne maximale de la matrice d'attention normalisée, (2) la proportion de normes de ligne dans la matrice d'attention non normalisée après suppression des entrées volumineuses. Ils utilisent ces paramètres fins pour refléter la difficulté du problème. Tant que les paramètres ci-dessus sont petits, l'algorithme d'échantillonnage temporel linéaire peut être implémenté même si la matrice a des entrées illimitées ou un grand rang stable.
HyperAttention a les caractéristiques d'une conception modulaire et peut être facilement intégré à d'autres implémentations sous-jacentes rapides. , en particulier c'est FlashAttention. Empiriquement, Super Attention surpasse les méthodes existantes lors de l'utilisation de l'algorithme LSH pour identifier les entrées volumineuses et permet d'obtenir des améliorations de vitesse significatives par rapport aux solutions de pointe telles que FlashAttention. Les chercheurs ont vérifié les performances d'HyperAttention sur une variété d'ensembles de données contextuelles de différentes longueurs
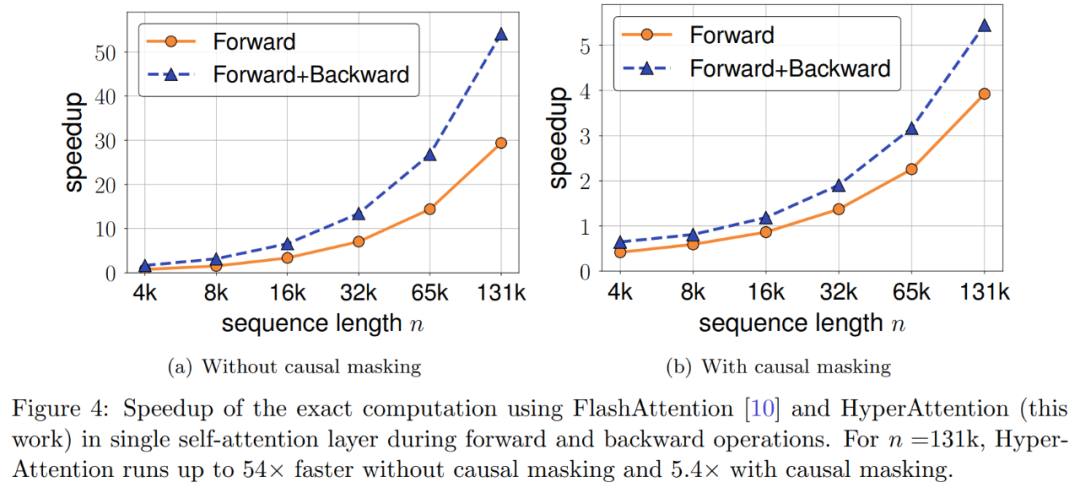
Par exemple, HyperAttention a rendu le temps d'inférence de ChatGLM2 50 % plus rapide sur une longueur de contexte de 32 000, tandis que la perplexité est passée de 5,6 à 6,3. HyperAttention est 5 fois plus rapide sur une seule couche d'attention avec des longueurs de contexte plus grandes (par exemple 131 000) et des masques causals.
Présentation de la méthode
L'attention du produit Dot implique le traitement de trois matrices d'entrée : Q (requêtes), K (clé), V (valeur), toutes de taille nxd, où n est le nombre de jetons dans la séquence d'entrée. , d est la dimensionnalité de la représentation sous-jacente. Le résultat de ce processus est le suivant :
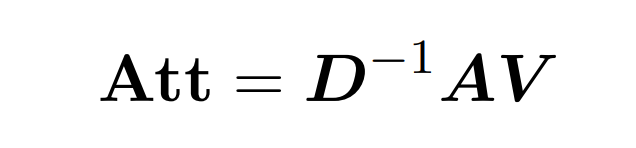
Ici, la matrice A := exp (QK^T) est définie comme l'indice d'élément de QK^T. D est une matrice diagonale n×n dérivée de la somme des lignes de A, où 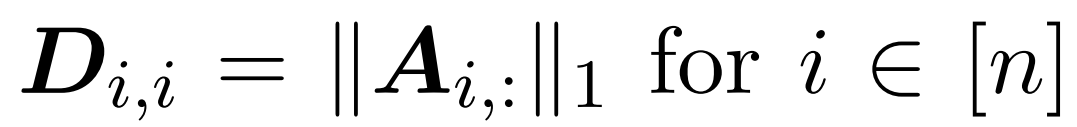 . Dans ce cas, la matrice A est appelée « matrice d'attention » et (D^-1) A est appelée « matrice softmax ». Il convient de noter que le calcul direct de la matrice d'attention A nécessite Θ(n²d) opérations, tandis que son stockage consomme Θ(n²) mémoire. Par conséquent, le calcul direct d’Att nécessite un temps d’exécution Ω(n²d) et une mémoire Ω(n²).
. Dans ce cas, la matrice A est appelée « matrice d'attention » et (D^-1) A est appelée « matrice softmax ». Il convient de noter que le calcul direct de la matrice d'attention A nécessite Θ(n²d) opérations, tandis que son stockage consomme Θ(n²) mémoire. Par conséquent, le calcul direct d’Att nécessite un temps d’exécution Ω(n²d) et une mémoire Ω(n²).
L’objectif du chercheur est d’approcher efficacement la matrice de sortie Att tout en conservant ses caractéristiques spectrales. Leur stratégie consiste à concevoir un estimateur efficace en temps quasi-linéaire pour la matrice D à échelle diagonale. De plus, ils se rapprochent rapidement du produit matriciel de la matrice softmax D^-1A par sous-échantillonnage. Plus précisément, ils visent à trouver une matrice d'échantillonnage 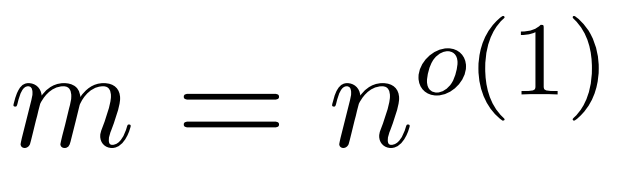 avec un nombre fini de lignes
avec un nombre fini de lignes 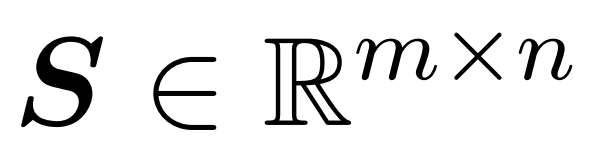 et une matrice diagonale
et une matrice diagonale 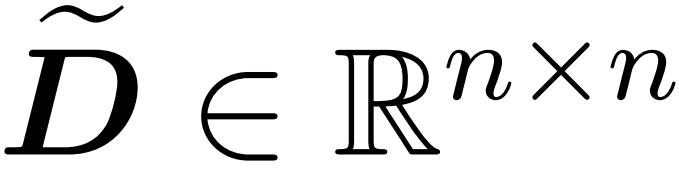 telle que les contraintes suivantes sur la spécification de l'opérateur de l'erreur soient satisfaites :
telle que les contraintes suivantes sur la spécification de l'opérateur de l'erreur soient satisfaites :
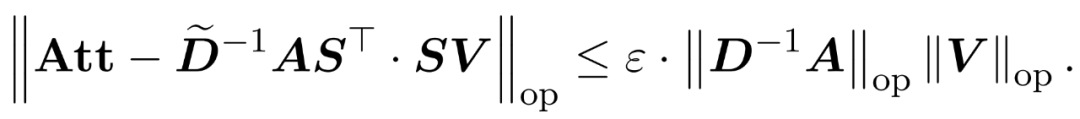
Les chercheurs ont montré qu'en définissant la matrice d'échantillonnage S basée sur la spécification de ligne de V, la partie multiplication matricielle du problème d'approximation de l'attention dans la formule (1) peut être résolue efficacement. Le problème le plus difficile est : comment obtenir une approximation fiable de la matrice diagonale D. Dans des résultats récents, Zandieh exploite efficacement le solveur rapide de KDE pour obtenir des approximations de haute qualité de D. Nous avons simplifié le programme KDEformer et démontré qu'un échantillonnage uniforme est suffisant pour obtenir les garanties spectrales requises sans avoir besoin d'un échantillonnage d'importance basé sur la densité du noyau. Cette simplification significative leur a permis de développer un algorithme en temps linéaire pratique et prouvable.
Contrairement aux recherches précédentes, notre méthode ne nécessite pas d'entrées limitées ni de classements stables limités. De plus, même si les entrées ou les rangs stables dans la matrice d’attention sont grands, les paramètres fins introduits pour analyser la complexité temporelle peuvent encore être petits.
En conséquence, HyperAttention est nettement plus rapide, avec une propagation avant et arrière plus de 50 fois plus rapide lorsque la longueur de la séquence est n = 131k. La méthode atteint toujours une accélération substantielle de 5 fois lorsqu’il s’agit de masques causals. De plus, lorsque la méthode est appliquée à un LLM pré-entraîné (tel que chatqlm2-6b-32k) et évaluée sur l'ensemble de données de référence à contexte long LongBench, elle maintient un niveau de performance proche du modèle d'origine même sans avoir besoin d'un réglage fin. . Les chercheurs ont également évalué des tâches spécifiques et ont constaté que les tâches de résumé et de complétion de code avaient un impact plus important sur les couches attentionnelles approximatives que les tâches de résolution de problèmes.
Algorithme
Afin d'obtenir une garantie de spectre lors de l'approximation de Att, la première étape de cet article consiste à effectuer une approximation 1 ± ε sur les termes diagonaux de la matrice D. Le produit matriciel entre A et V est ensuite approximé par échantillonnage (D^-1) selon la rangée carrée ℓ₂-normes de V.
Le processus d'approximation de D se compose de deux étapes. Premièrement, un algorithme basé sur le tri LSH de Hamming est utilisé pour identifier les entrées principales dans la matrice d'attention, comme le montre la définition 1. La deuxième étape consiste à sélectionner aléatoirement un petit sous-ensemble de K. Cet article montrera que, sous certaines hypothèses modérées sur les matrices A et D, cette méthode simple peut établir les limites spectrales des matrices estimées. L'objectif du chercheur est de trouver une matrice approchée D suffisamment précise pour satisfaire :

L'hypothèse de cet article est que la norme de colonne de la matrice softmax présente une distribution relativement uniforme. Plus précisément, le chercheur suppose que pour tout i ∈ [n] t il existe des 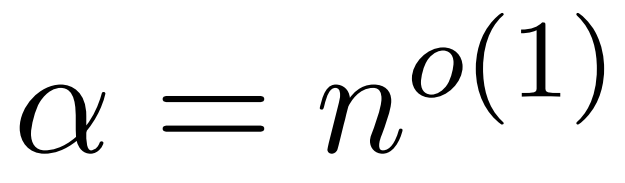 tels que
tels que 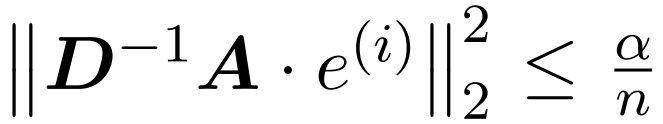 .
.
La première étape de l'algorithme consiste à identifier les entrées volumineuses dans la matrice d'attention A en hachant les clés et les requêtes dans des compartiments de taille uniforme à l'aide du LSH trié par Hamming (sortLSH). L'algorithme 1 détaille ce processus et la figure 1 l'illustre visuellement.
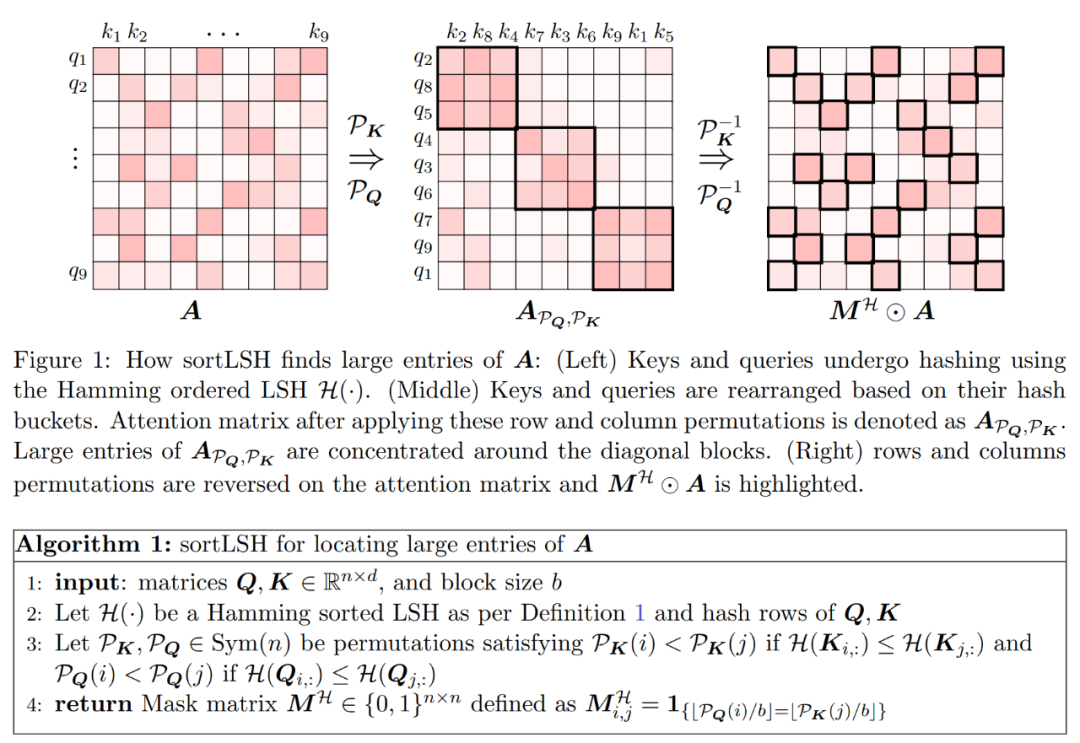
La fonction de l'algorithme 1 est de renvoyer un masque clairsemé utilisé pour isoler les entrées principales de la matrice d'attention. Après avoir obtenu ce masque, le chercheur peut calculer une approximation de la matrice D dans l'algorithme 2 qui satisfait à la garantie spectrale de l'équation (2). L'algorithme est mis en œuvre en combinant la valeur d'attention correspondant au masque avec un ensemble de colonnes sélectionnées au hasard dans la matrice d'attention. L'algorithme présenté dans cet article peut être largement appliqué et utilisé efficacement en utilisant des masques prédéfinis pour spécifier la position des entrées principales dans la matrice d'attention. La principale garantie de l'algorithme est donnée dans le Théorème 1. Un sous-programme intégrant la diagonale approchée
et le produit matriciel entre l'approchée 
et la matrice de valeurs V. Par conséquent, les chercheurs ont introduit HyperAttention, un algorithme efficace qui peut se rapprocher du mécanisme d’attention de la formule (1) avec une garantie de spectre en un temps approximativement linéaire. L'algorithme 3 prend en entrée un masque MH qui définit la position de l'entrée dominante dans la matrice d'attention. Ce masque peut être généré à l'aide de l'algorithme sortLSH (algorithme 1) ou peut être un masque prédéfini, similaire à l'approche de [7]. Nous supposons que le grand masque d'entrée M^H est clairsemé de par sa conception et que son nombre d'entrées non nulles est limité
.
Comme le montre la figure 2, cette méthode repose sur une observation importante. L'attention masquée M^C⊙A peut être décomposée en trois matrices non nulles, dont chacune fait la moitié de la taille de la matrice d'attention d'origine. Le bloc A_21 complètement en dessous de la diagonale est une attention non masquée. Par conséquent, nous pouvons approximer sa somme de lignes en utilisant l’algorithme 2. 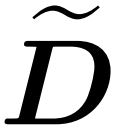 Les deux blocs diagonaux
Les deux blocs diagonaux 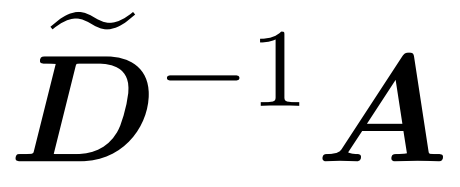 et
et 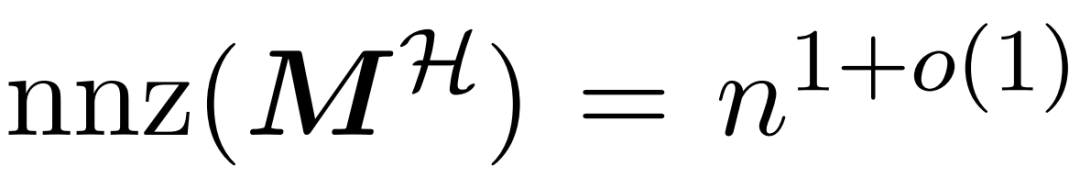 montrés sur la figure 2 sont des attentions causales, qui font la moitié de la taille originale. Pour traiter ces relations causales, les chercheurs ont utilisé une approche récursive, en les divisant en morceaux plus petits et en répétant le processus. Le pseudocode de ce processus est donné dans l'algorithme 4.
montrés sur la figure 2 sont des attentions causales, qui font la moitié de la taille originale. Pour traiter ces relations causales, les chercheurs ont utilisé une approche récursive, en les divisant en morceaux plus petits et en répétant le processus. Le pseudocode de ce processus est donné dans l'algorithme 4.
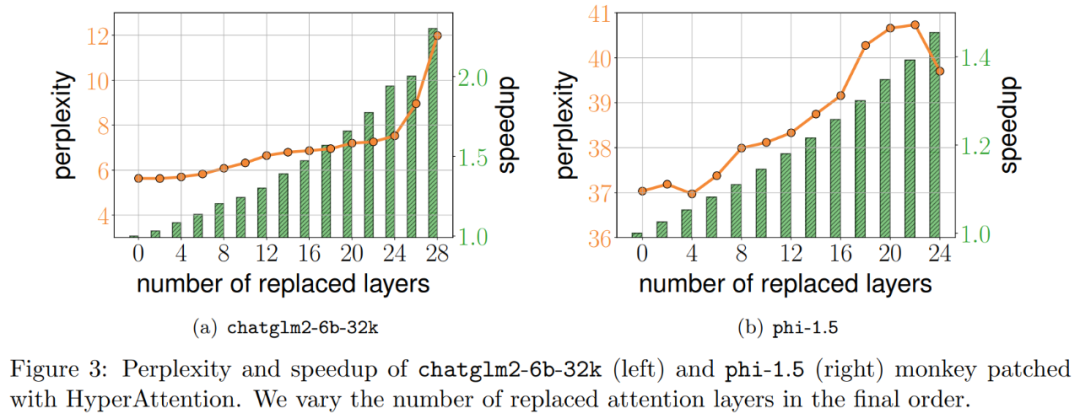
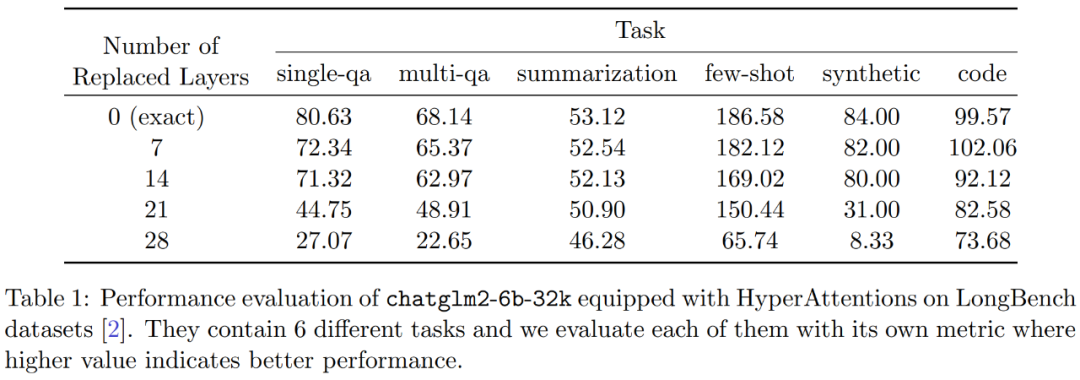
Expériences et résultats Afin de conserver le sens original inchangé, le contenu doit être réécrit en chinois et la phrase originale n'a pas besoin d'apparaître Les chercheurs ont d'abord évalué HyperAttention sur deux LLM pré-entraînés, et a sélectionné celui qui est largement utilisé dans les applications pratiques, deux modèles avec des architectures différentes : chatglm2-6b-32k et phi-1.5. En fonctionnement, ils corrigent la dernière couche d'attention ℓ en la remplaçant par HyperAttention, où le nombre de ℓ peut varier de 0 au nombre total de toutes les couches d'attention dans chaque LLM. Notez que l'attention dans les deux modèles nécessite un masque causal et que l'algorithme 4 est appliqué de manière récursive jusqu'à ce que la longueur de la séquence d'entrée n soit inférieure à 4 096. Pour toutes les longueurs de séquence, nous définissons la taille du bucket b et le nombre de colonnes échantillonnées m sur 256. Ils ont évalué les performances de ces modèles de singes patchés en termes de perplexité et d'accélération. Dans le même temps, les chercheurs ont utilisé LongBench, une collection d'ensembles de données de référence contextuelles longues, qui contient 6 tâches différentes, à savoir la réponse à des questions uniques/multi-documents, la synthèse, l'apprentissage de petits échantillons, les tâches de synthèse et l'achèvement du code. Ils ont sélectionné un sous-ensemble de l’ensemble de données avec une longueur de séquence de codage supérieure à 32 768 et l’ont élagué si la longueur dépassait 32 768. Calculez ensuite la perplexité de chaque modèle, qui est la perte de prédiction du prochain jeton. Pour mettre en évidence l'évolutivité des séquences longues, nous avons également calculé l'accélération totale sur toutes les couches d'attention, qu'elles soient effectuées par HyperAttention ou FlashAttention. Les résultats présentés dans la figure 3 ci-dessus sont les suivants. Même si chatglm2-6b-32k a passé le patch HyperAttention, il montre toujours un degré raisonnable de confusion. Par exemple, après avoir remplacé la couche 20, la perplexité augmente d'environ 1 et continue d'augmenter lentement jusqu'à atteindre la couche 24. Le temps d'exécution de la couche d'attention a été amélioré d'environ 50 %. Si toutes les couches sont remplacées, la perplexité s'élève à 12 et s'exécute 2,3 fois plus vite. Le modèle phi-1,5 montre également une situation similaire, mais à mesure que le nombre d'HyperAttention augmente, la perplexité augmentera de manière linéaire De plus, les chercheurs ont également mené le chatglm2-6b-32k patché par singe sur l'ensemble de données LongBench. Une évaluation des performances a été effectuée et les scores d'évaluation pour les tâches respectives telles que la réponse à des questions uniques/multidocuments, le résumé, l'apprentissage par petits échantillons, les tâches de synthèse et l'achèvement du code ont été calculés. Les résultats de l'évaluation sont présentés dans le tableau 1 ci-dessous Bien que le remplacement d'HyperAttention entraîne généralement une pénalité de performances, ils ont observé que son impact varie en fonction de la tâche à accomplir. Par exemple, la synthèse et la complétion de code sont les plus robustes par rapport aux autres tâches. Ce qui est remarquable, c'est que lorsque la moitié des couches d'attention (soit 14 couches) sont corrigées, les chercheurs ont confirmé que la baisse de performance pour la plupart des tâches ne dépassera pas 13 %. En particulier pour la tâche récapitulative, les performances restent presque inchangées, ce qui indique que cette tâche est la plus robuste aux modifications partielles du mécanisme d'attention. Lorsque n = 32k, la vitesse de calcul de la couche d'attention est augmentée de 1,5 fois. Couche unique d'auto-attention Les chercheurs ont exploré plus en détail l'accélération de l'hyperattention lorsque la longueur de la séquence variait de 4 096 à 131 072. Ils ont mesuré l’heure murale des opérations avant et avant et arrière lorsqu’elles sont calculées à l’aide de FlashAttention ou accélérées par HyperAttention. L’heure de l’horloge murale avec et sans masquage causal a également été mesurée. Toutes les entrées Q, K et V ont la même longueur, la dimensionnalité est fixée à d = 64 et le nombre de têtes d'attention est de 12. Ils choisissent les mêmes paramètres qu'avant dans HyperAttention. Comme le montre la figure 4, lorsque le masque causal n'est pas appliqué, la vitesse de l'HyperAttention est augmentée de 54 fois, et avec le masque causal, la vitesse est augmentée de 5,4 fois. Bien que la perplexité temporelle du masquage causal et du non-masquage soit la même, l'algorithme actuel de masquage causal (algorithme 1) nécessite des opérations supplémentaires telles que le partitionnement de Q, K et V, la fusion des sorties d'attention, ce qui entraîne une augmentation du temps d'exécution réel. Lorsque la longueur de la séquence n augmente, l'accélération sera plus élevée Les chercheurs pensent que ces résultats ne sont pas seulement applicables à l'inférence, mais peuvent également être utilisés pour entraîner ou affiner le LLM afin de s'adapter à des séquences plus longues, ce qui ouvre l'expansion de l'attention personnelle Nouvelles possibilités  Les chercheurs ont comparé l'algorithme en étendant le grand modèle de langage existant pour traiter des séquences à longue portée. Toutes les expériences ont été exécutées sur un seul GPU A100 de 40 Go et ont utilisé FlashAttention 2 pour un calcul précis de l'attention.
Les chercheurs ont comparé l'algorithme en étendant le grand modèle de langage existant pour traiter des séquences à longue portée. Toutes les expériences ont été exécutées sur un seul GPU A100 de 40 Go et ont utilisé FlashAttention 2 pour un calcul précis de l'attention. 
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Qu'est-ce qu'un tas ? Quel est le domaine de la méthode ? Introduction à la zone de tas et de méthode dans le modèle de mémoire JVM
- Quel est le modèle de boîte CSS ?
- Quels sont les quatre modèles courants de développement de logiciels ?
- Comment copier un modèle dans un autre fichier dans 3dmax
- Les programmeurs sont en danger ! On dit qu'OpenAI recrute des troupes d'externalisation dans le monde entier et forme étape par étape les agriculteurs de code ChatGPT.

