Quel est le plus grand triangle de Reuleaux à l'intérieur d'un carré inscrit dans une ellipse ?

Ici, nous verrons l'aire d'un plus grand triangle de la Ruhr qui s'inscrit dans un carré qui s'inscrit dans une ellipse. Nous savons que la longueur du grand axe de l’ellipse est 2a et la longueur du petit axe est 2b. La longueur du côté du carré est « x » et la hauteur du triangle Luer est h.

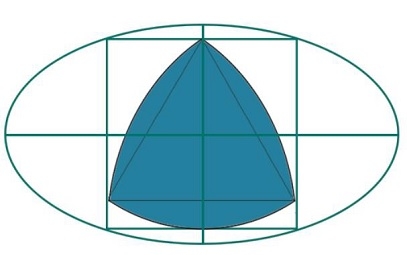
Nous savons que la longueur du côté du carré inscrit dans l'ellipse de grand axe 2a et de petit axe 2b est −

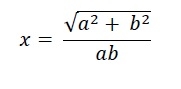
La hauteur du triangle de la Ruhr est la même que a. Donc h = x. L’aire du triangle de la Ruhr est donc −

.

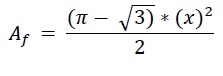Exemple

#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float a, float b) { //a and b are half of major and minor axis of ellipse
   if (a < 0 || b < 0) //either a or b is negative it is invalid
      return -1;
   float x = sqrt((a*a) + (b*b)) / (a*b);
   float area = ((3.1415 - sqrt(3)) * (x) * (x))/2;
   return area;
}
int main() {
   float a = 5;
   float b = 4;
   cout << "Area of Reuleaux Triangle: " << areaReuleaux(a, b);
}

Sortie

Area of Reuleaux Triangle: 0.0722343

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!