Intégration de modèles de séries chronologiques pour améliorer la précision des prévisions

Utilisez Catboost pour extraire les signaux des modèles RNN, ARIMA et Prophet à des fins de prédiction.

L'intégration de divers apprenants faibles peut améliorer la précision des prédictions, mais si notre modèle est déjà très puissant, l'apprentissage d'ensemble peut souvent être la cerise sur le gâteau. La populaire bibliothèque d'apprentissage automatique scikit-learn fournit un StackingRegressor qui peut être utilisé pour les tâches de séries chronologiques. Mais StackingRegressor a une limitation : il n'accepte que d'autres classes de modèles et API scikit-learn. Ainsi, les modèles comme ARIMA qui ne sont pas disponibles dans scikit-learn, ou les modèles issus de réseaux de neurones profonds ne peuvent pas être utilisés. Dans cet article, je vais montrer comment empiler les prédictions du modèle que nous pouvons voir.

Nous utiliserons le package suivant :

pip install --upgrade scalecast
 conda install tensorflow
 conda install shap
 conda install -c conda-forge cmdstanpy
 pip install prophet

Ensemble de données

L'ensemble de données est divisé en un ensemble d'entraînement (700 observations) et un ensemble de test (48 observations) toutes les heures. Le code suivant lit les données et les stocke dans un objet Forecaster :

import pandas as pd
 import numpy as np
 from scalecast.Forecaster import Forecaster
 from scalecast.util import metrics
 import matplotlib.pyplot as plt
 import seaborn as sns
 
 def read_data(idx = 'H1', cis = True, metrics = ['smape']):
 info = pd.read_csv(
 'M4-info.csv',
 index_col=0,
 parse_dates=['StartingDate'],
 dayfirst=True,
)
 train = pd.read_csv(
 f'Hourly-train.csv',
 index_col=0,
).loc[idx]
 test = pd.read_csv(
 f'Hourly-test.csv',
 index_col=0,
).loc[idx]
 y = train.values
 sd = info.loc[idx,'StartingDate']
 fcst_horizon = info.loc[idx,'Horizon']
 cd = pd.date_range(
 start = sd,
 freq = 'H',
 periods = len(y),
)
 f = Forecaster(
 y = y, # observed values
 current_dates = cd, # current dates
 future_dates = fcst_horizon, # forecast length
 test_length = fcst_horizon, # test-set length
 cis = cis, # whether to evaluate intervals for each model
 metrics = metrics, # what metrics to evaluate
)
 
 return f, test.values
 
 f, test_set = read_data()
 f # display the Forecaster object

Le résultat est le suivant :

Model

Avant de commencer à construire le modèle, nous devons en générer la prédiction la plus simple. , la méthode naïve consiste à transmettre les 24 dernières observations.

f.set_estimator('naive')
 f.manual_forecast(seasonal=True)

Ensuite, utilisez ARIMA, LSTM et Prophet comme références.

ARIMA

La moyenne mobile intégrée autorégressive est une technique de série chronologique populaire et simple qui utilise le décalage et l'erreur d'une série pour prédire son avenir de manière linéaire. Grâce à EDA, nous avons déterminé que cette série est très saisonnière. J'ai donc finalement choisi d'appliquer le modèle saisonnier ARIMA d'ordre (5,1,4) x(1,1,1,24).

f.set_estimator('arima')
 f.manual_forecast(
order = (5,1,4),
seasonal_order = (1,1,1,24),
call_me = 'manual_arima',
 )

LSTM

Si ARIMA est un modèle de série chronologique relativement simple, alors LSTM est l'une des méthodes les plus avancées. Il s'agit d'une technique d'apprentissage en profondeur comportant de nombreux paramètres, notamment un mécanisme permettant de découvrir des modèles à long terme et à court terme dans des données séquentielles, ce qui la rend théoriquement idéale pour les séries chronologiques. Voici l'utilisation de tensorflow pour construire ce modèle

f.set_estimator('rnn')
 f.manual_forecast(
 lags = 48,
 layers_struct=[
('LSTM',{'units':100,'activation':'tanh'}),
('LSTM',{'units':100,'activation':'tanh'}),
('LSTM',{'units':100,'activation':'tanh'}),
],
 optimizer = 'Adam',
 epochs = 15,
 plot_loss = True,
 validation_split=0.2,
 call_me = 'rnn_tanh_activation',
 )
 
 f.manual_forecast(
 lags = 48,
 layers_struct=[
('LSTM',{'units':100,'activation':'relu'}),
('LSTM',{'units':100,'activation':'relu'}),
('LSTM',{'units':100,'activation':'relu'}),
],
 optimizer = 'Adam',
 epochs = 15,
 plot_loss = True,
 validation_split=0.2,
 call_me = 'rnn_relu_activation',
 )

Prophet

Malgré sa popularité, certains prétendent que sa précision n'est pas impressionnante, principalement parce que son inférence de tendances est parfois irréaliste et qu'elle ne prend pas en compte les modèles locaux via autorégression modélisation. Mais il a aussi ses propres caractéristiques. 1. Il applique automatiquement les effets des vacances au modèle et prend également en compte plusieurs types de saisonnalité. Tout cela peut être fait avec le minimum requis par l'utilisateur, j'aime donc l'utiliser comme signal plutôt que comme prédiction finale.

f.set_estimator('prophet')
 f.manual_forecast()

Comparaison des résultats

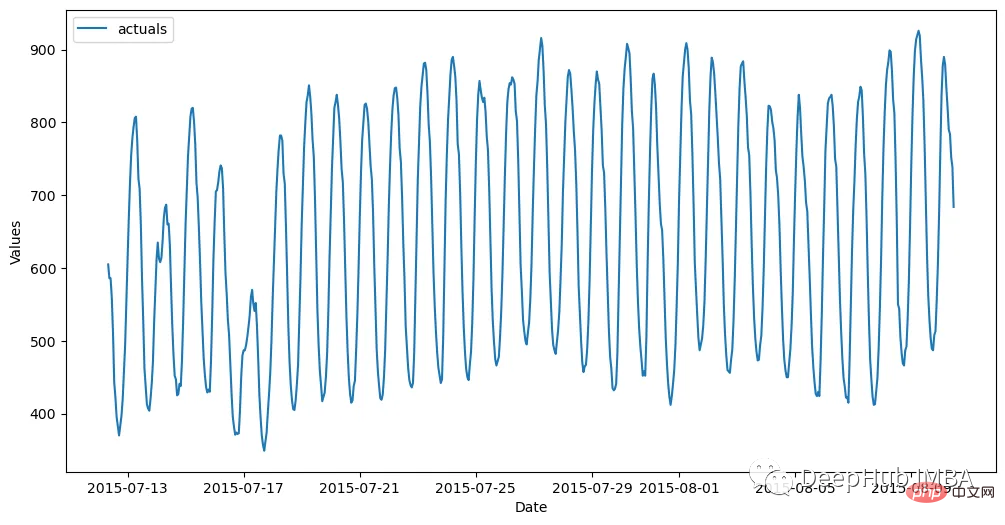
Maintenant que nous avons généré des prédictions pour chaque modèle, voyons comment ils fonctionnent sur l'ensemble de validation, qui correspond aux 48 dernières observations de notre ensemble d'entraînement.

results = f.export(determine_best_by='TestSetSMAPE')
 ms = results['model_summaries']
 ms[
[
 'ModelNickname',
 'TestSetLength',
 'TestSetSMAPE',
 'InSampleSMAPE',
]
 ]

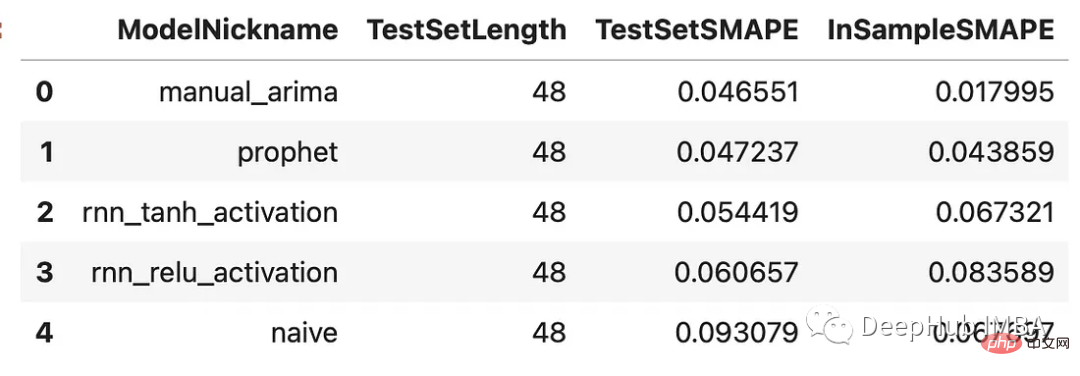
Chaque modèle surpasse la méthode naïve. Le modèle ARIMA a obtenu les meilleurs résultats avec un pourcentage d'erreur de 4,7 %, suivi du modèle Prophet. Jetons un coup d'œil à toutes les prédictions par rapport à l'ensemble de validation :

f.plot(order_by="TestSetSMAPE",ci=True)
 plt.show()

Tous ces modèles fonctionnent raisonnablement bien sur cette série chronologique, il n'y a pas de grands écarts entre eux. Empilons-les !

Modèles empilés

Chaque modèle empilé nécessite un estimateur final qui filtrera les différentes estimations des autres modèles, créant ainsi un nouvel ensemble de prédictions. Nous superposerons les résultats précédents avec l'estimateur Catboost. Catboost est un programme puissant et on espère qu'il enrichira le meilleur signal de chaque modèle appliqué.

f.add_signals(
 f.history.keys(), # add signals from all previously evaluated models
 )
 f.add_ar_terms(48)
 f.set_estimator('catboost')

Le code ci-dessus ajoute les prédictions de chaque modèle évalué à un objet Forecaster. Il appelle ces prédictions des « signaux ». Elles sont traitées de la même manière que toutes les autres covariables stockées dans le même objet. Les 48 dernières séries de décalages sont également ajoutées ici en tant que régresseurs supplémentaires que le modèle Catboost peut utiliser pour faire des prédictions. Appelons maintenant trois modèles Catboost : un utilisant tous les signaux et décalages disponibles, un utilisant uniquement les signaux et un utilisant uniquement les décalages.

f.manual_forecast(
 Xvars='all',
 call_me='catboost_all_reg',
 verbose = False,
 )
 f.manual_forecast(
 Xvars=[x for x in f.get_regressor_names() if x.startswith('AR')],
 call_me = 'catboost_lags_only',
 verbose = False,
 )
 f.manual_forecast(
 Xvars=[x for x in f.get_regressor_names() if not x.startswith('AR')],
 call_me = 'catboost_signals_only',
 verbose = False,
 )

Ci-dessous vous pouvez comparer les résultats de tous les modèles. Nous examinerons deux métriques : le SMAPE et l'erreur d'échelle absolue moyenne (MASE). Ce sont deux mesures utilisées dans la compétition M4 réelle.

test_results = pd.DataFrame(index = f.history.keys(),columns = ['smape','mase'])
 for k, v in f.history.items():
 test_results.loc[k,['smape','mase']] = [
 metrics.smape(test_set,v['Forecast']),
 metrics.mase(test_set,v['Forecast'],m=24,obs=f.y),
]
 
 test_results.sort_values('smape')

可以看到，通过组合来自不同类型模型的信号生成了两个优于其他估计器的估计器:使用所有信号训练的Catboost模型和只使用信号的Catboost模型。这两种方法的样本误差都在2.8%左右。下面是对比图：

fig, ax = plt.subplots(figsize=(12,6))
 f.plot(
 models = ['catboost_all_reg','catboost_signals_only'],
 ci=True,
 ax = ax
 )
 sns.lineplot(
 x = f.future_dates,
 y = test_set,
 ax = ax,
 label = 'held out actuals',
 color = 'darkblue',
 alpha = .75,
 )
 plt.show()

哪些信号最重要?

为了完善分析，我们可以使用shapley评分来确定哪些信号是最重要的。Shapley评分被认为是确定给定机器学习模型中输入的预测能力的最先进的方法之一。得分越高，意味着输入在特定模型中越重要。

f.export_feature_importance('catboost_all_reg')

上面的图只显示了前几个最重要的预测因子，但我们可以从中看出，ARIMA信号是最重要的，其次是序列的第一个滞后，然后是Prophet。RNN模型的得分也高于许多滞后模型。如果我们想在未来训练一个更轻量的模型，这可能是一个很好的起点。

总结

在这篇文章中，我展示了在时间序列上下文中集成模型的力量，以及如何使用不同的模型在时间序列上获得更高的精度。这里我们使用scalecast包，这个包的功能还是很强大的，如果你喜欢，可以去它的主页看看：https://github.com/mikekeith52/scalecast

本文的数据集是M4的时序竞赛：https://github.com/Mcompetitions/M4-methods

使用代码在这里：https://scalecast-examples.readthedocs.io/en/latest/misc/stacking/custom_stacking.html

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!