Maison >Périphériques technologiques >IA >Une solution en environnement ouvert qui résout des lacunes telles que la couche Batch Norm
Une solution en environnement ouvert qui résout des lacunes telles que la couche Batch Norm
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-04-26 10:01:07993parcourir
La méthode Test-Time Adaptation (TTA) guide le modèle pour effectuer un apprentissage rapide non supervisé/auto-supervisé pendant la phase de test. Il s'agit actuellement d'un outil puissant et efficace pour améliorer les capacités de généralisation hors distribution des modèles profonds. Cependant, dans les scénarios ouverts dynamiques, une stabilité insuffisante reste un défaut majeur des méthodes TTA existantes, ce qui entrave sérieusement leur déploiement pratique. À cette fin, une équipe de recherche de l'Université de technologie de Chine du Sud, du Tencent AI Lab et de l'Université nationale de Singapour a analysé les raisons pour lesquelles la méthode TTA existante est instable dans des scénarios dynamiques dans une perspective unifiée, et a souligné que la couche de normalisation qui s'appuie sur sur Batch conduit à l'instabilité. L'une des principales raisons de la stabilité. De plus, certains échantillons avec du bruit/des gradients à grande échelle dans le flux de données de test peuvent facilement optimiser le modèle pour obtenir une solution triviale dégénérée. Sur cette base, une méthode SAR de minimisation de l'entropie au temps de test, sensible à la netteté et fiable, est en outre proposée pour obtenir une migration en ligne et une généralisation stables et efficaces du modèle de temps de test dans des scénarios ouverts dynamiques. Ce travail a été sélectionné dans l'ICLR 2023 Oral (Top-5% parmi les articles acceptés).

- Titre de l'article : Vers une adaptation stable au temps de test dans un monde sauvage dynamique
- Adresse de l'article : https://openreview.net/forum?id=g2YraF75Tj
- Ouvert Code source : https://github.com/mr-eggplant/SAR
Qu'est-ce que l'adaptation au temps de test ?
La technologie traditionnelle d'apprentissage automatique apprend généralement sur une grande quantité de données d'entraînement collectées à l'avance, puis corrige le modèle pour la prédiction d'inférence. Ce paradigme atteint souvent de très bonnes performances lorsque les données de test et d'entraînement proviennent de la même distribution de données. Cependant, dans les applications pratiques, la distribution des données de test peut facilement s'écarter de la distribution des données d'entraînement d'origine (changement de distribution). Par exemple, lors de la collecte de données de test : 1) Les changements météorologiques font que l'image contient de la pluie, de la neige, et occlusion du brouillard ; 2) L'image est floue en raison d'une prise de vue incorrecte, ou l'image contient du bruit en raison de la dégradation du capteur ; 3) Le modèle a été formé sur la base de données collectées dans les villes du nord, mais a été déployé dans les villes du sud ; Les situations ci-dessus sont très courantes, mais elles sont souvent fatales pour les modèles profonds, car leurs performances peuvent chuter considérablement dans ces scénarios, limitant sérieusement leur utilisation dans le monde réel (en particulier les applications à haut risque telles que la conduite autonome) et leur déploiement à grande échelle.
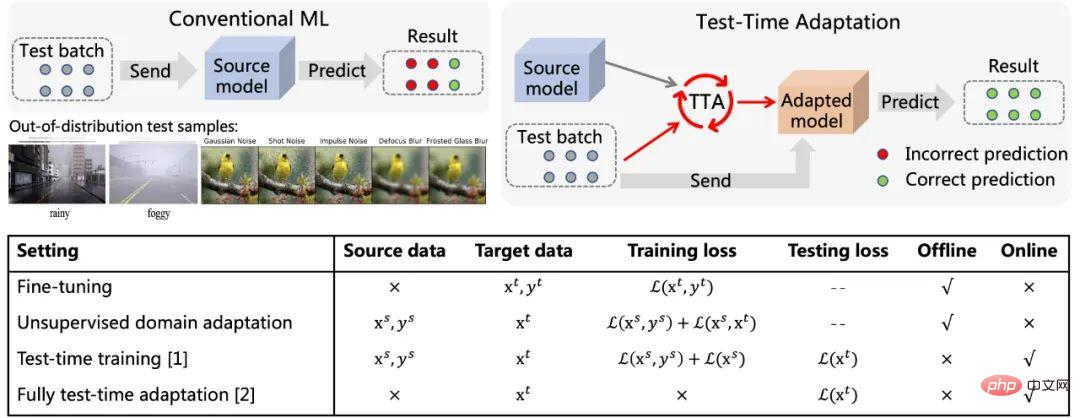
Figure 1 Diagramme schématique de l'adaptation du temps de test (voir [5]) et sa comparaison avec les caractéristiques des méthodes existantes
est différent du paradigme d'apprentissage automatique traditionnel , comme le montre la figure 1. Une fois l'échantillon de test arrivé, l'adaptation du temps de test (TTA) utilise d'abord une méthode auto-supervisée ou non supervisée pour affiner le modèle en fonction des données, puis utilise le modèle mis à jour pour effectuer la prédiction finale. . Les objectifs typiques d'apprentissage auto/non supervisé incluent : la prédiction de rotation, l'apprentissage contrastif, la minimisation de l'entropie, etc. Ces méthodes démontrent toutes d’excellentes performances de généralisation hors distribution. Par rapport aux méthodes traditionnelles de réglage fin et d'adaptation de domaine non supervisée, l'adaptation au moment du test peut réaliser une migration en ligne, qui est plus efficace et plus universelle. De plus, la méthode complète d'adaptation du temps de test [2] peut s'adapter à n'importe quel modèle pré-entraîné sans avoir besoin de données d'entraînement originales ni d'interférence avec le processus d'entraînement d'origine du modèle. Les avantages ci-dessus ont considérablement amélioré la polyvalence pratique de la méthode TTA. Associés à ses excellentes performances, la TTA est devenue une direction de recherche extrêmement prisée dans les domaines de la migration, de la généralisation et d'autres domaines connexes. Bien que les méthodes TTA existantes aient montré un grand potentiel de généralisation hors distribution, cette excellente performance est souvent obtenue dans certaines conditions de test spécifiques, par exemple, les échantillons du flux de données de test. au cours d'une période donnée, tous proviennent du même type de changement de distribution, la véritable distribution des catégories des échantillons de test est uniforme et aléatoire, et chaque fois, un échantillon en mini-lot est requis avant que l'adaptation puisse être effectuée. Mais en fait, ces hypothèses potentielles ci-dessus sont difficiles à toujours satisfaire dans le monde ouvert réel. En pratique, le flux de données de test peut arriver dans n'importe quelle combinaison, et idéalement le modèle ne doit faire aucune hypothèse sur la forme d'arrivée du flux de données de test. Comme le montre la figure 2, il est tout à fait possible que le flux de données de test rencontre : (a) les échantillons proviennent de différents décalages de distribution (c'est-à-dire des décalages d'échantillons mixtes (b) ; taille du lot d'échantillons Très petite (même 1) ; (c) La véritable répartition des classes des échantillons sur une période de temps est inégale et change de manière dynamique . Cet article fait référence collectivement au TTA dans le scénario ci-dessus sous le nom de Wild TTA. Malheureusement, les méthodes TTA existantes semblent souvent fragiles et instables dans ces scénarios sauvages, avec des performances de migration limitées et peuvent même nuire aux performances du modèle d'origine. Par conséquent, si nous voulons réellement réaliser le déploiement d’applications à grande échelle et en profondeur de la méthode TTA dans des scénarios réels, la résolution du problème Wild TTA est une partie inévitable et importante. Figure 2 Scène ouverte dynamique en adaptation lors des tests sur modèle#🎜 🎜# Cet article analyse les raisons de l'échec du TTA dans de nombreux scénarios Wild d'un point de vue unifié, puis proposez une solution. 1. Pourquoi Wild TTA est-il instable ? (1) La normalisation par lots (BN) est l'une des principales raisons de l'instabilité du TTA dans les scénarios dynamiques : Existant Les méthodes TTA sont généralement basées sur l'adaptation des statistiques BN, c'est-à-dire sur l'utilisation de données de test pour calculer la moyenne et l'écart type dans la couche BN. Cependant, dans les trois scénarios dynamiques réels, la précision de l'estimation statistique au sein de la couche BN sera biaisée, ce qui entraînera un TTA instable : : Étant donné que les statistiques de BN représentent en fait une certaine distribution de données de test, l'utilisation d'un ensemble de paramètres statistiques pour estimer plusieurs distributions en même temps conduira inévitablement à des performances limitées, voir Figure 3 ; #Scénario (b) : Les statistiques du BN dépendent de la taille du lot. Il est difficile d'obtenir des estimations statistiques précises du BN sur des échantillons de petite taille, voir Figure 4 ; 🎜# Scénario (c) : les échantillons avec une distribution d'étiquettes déséquilibrée entraîneront un biais dans les statistiques au sein de la couche BN, c'est-à-dire que les statistiques sont biaisées vers une catégorie spécifique (une plus grande proportion du lot) Catégorie), voir Figure 5 ; Pourquoi une adaptation sauvage du temps de test ?
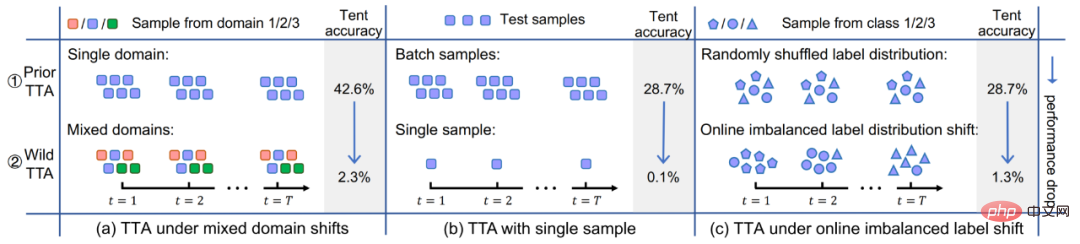

Figure 5 Performances de différentes méthodes et modèles (différentes couches de normalisation) lors du changement de distribution des étiquettes de déséquilibre en ligne. Plus le ratio de déséquilibre sur l'axe horizontal de la figure est élevé, plus le déséquilibre des étiquettes est grave.
(2) La minimisation de l'entropie en ligne peut facilement optimiser le modèle en une solution triviale dégénérée, c'est-à-dire prédire n'importe quel échantillon dans la même classe : selon les figures 6 (a) et (b), lorsque la distribution changements Lorsque le niveau est sévère (niveau 5), le phénomène de dégradation et d'effondrement du modèle se produit soudainement pendant le processus d'adaptation en ligne, c'est-à-dire que tous les échantillons (avec des catégories réelles différentes) sont prédits dans la même classe en même temps, la norme ; du gradient du modèle augmente rapidement avant et après l'effondrement du modèle, puis il chute à presque 0, comme le montre la figure 6(c), ce qui indique que certains gradients à grande échelle/bruit peuvent avoir détruit les paramètres du modèle, provoquant ainsi le modèle s'effondrer.

Figure 6 Analyse des cas d'échec dans la minimisation de l'entropie au moment du test en ligne
2. Méthode de minimisation de l'entropie au moment du test fiable et sensible à la netteté
Pour l'atténuation Pour résoudre le problème de dégradation du modèle ci-dessus, cet article propose une méthode de minimisation de l'entropie au temps de test fiable et sensible à la netteté (méthode de minimisation de l'entropie fiable et sensible à la netteté, SAR). Cela atténue ce problème de deux manières : 1) La minimisation fiable de l'entropie supprime certains échantillons qui génèrent des gradients importants/bruyants de la mise à jour adaptative du modèle ; 2) L'optimisation de la netteté du modèle rend le modèle correct pour Certains gradients de bruit ; générés dans les échantillons restants sont insensibles . Les détails spécifiques sont expliqués comme suit :
Minimisation fiable de l'entropie : établissez un indice de jugement alternatif pour la sélection du gradient basé sur l'entropie et excluez les échantillons à haute entropie (y compris les échantillons des zones 1 et 2 de la figure 6 (d) ) de l'adaptation du modèle Ne participez pas à la mise à jour du modèle sauf :

où x représente l'échantillon de test, Θ représente le paramètre du modèle, 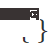 représente la fonction indicatrice,
représente la fonction indicatrice,  représente l'entropie de le résultat de la prédiction de l'échantillon,
représente l'entropie de le résultat de la prédiction de l'échantillon, 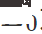 est le super paramètre. Seulement si
est le super paramètre. Seulement si 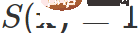
l'échantillon participera au calcul de rétropropagation.
Optimisation de l'entropie sensible à la netteté : les échantillons filtrés par un mécanisme de sélection d'échantillons fiable ne peuvent pas éviter de contenir encore des échantillons dans la zone 4 de la figure 6 (d), et ces échantillons peuvent générer du bruit/de grands gradients continuent le modèle d'interférence. À cette fin, cet article envisage d'optimiser le modèle au minimum afin qu'il puisse être insensible aux mises à jour du modèle causées par les gradients de bruit, c'est-à-dire qu'il n'affecte pas les performances de son modèle d'origine :
. 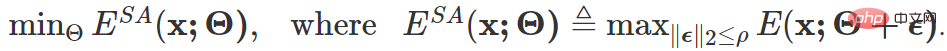
Les objectifs ci-dessus Le formulaire final de mise à jour du dégradé est le suivant :
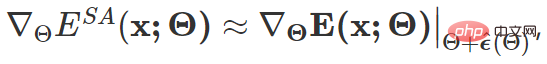
Parmi eux 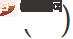 est inspiré de SAM [4] et est obtenu par solution approchée par développement de Taylor du premier ordre. Pour plus de détails, veuillez vous référer au texte original et au code de cet article.
est inspiré de SAM [4] et est obtenu par solution approchée par développement de Taylor du premier ordre. Pour plus de détails, veuillez vous référer au texte original et au code de cet article.
À ce stade, l'objectif d'optimisation global de cet article est le suivant :
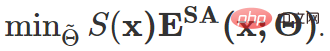
De plus, afin d'éviter que le système ci-dessus échoue encore dans des conditions extrêmes, une stratégie de récupération modèle est en outre introduit : surveillance du modèle via mobile. En cas d'effondrement de la dégradation, il est décidé de restaurer les valeurs d'origine des paramètres de mise à jour du modèle au moment nécessaire.
Évaluation expérimentale
Comparaison des performances dans des scénarios ouverts dynamiques
SAR est basé sur les trois scénarios ouverts dynamiques ci-dessus, à savoir a) changement de distribution du mélange, b) adaptation d'un échantillon unique et c) déséquilibre en ligne. le changement de distribution est vérifié expérimentalement sur l'ensemble de données ImageNet-C et les résultats sont présentés dans les tableaux 1, 2 et 3. SAR obtient des résultats remarquables dans les trois scénarios, en particulier dans les scénarios b) et c). SAR utilise VitBase comme modèle de base et sa précision dépasse de près de 10 % la méthode SOTA EATA actuelle.
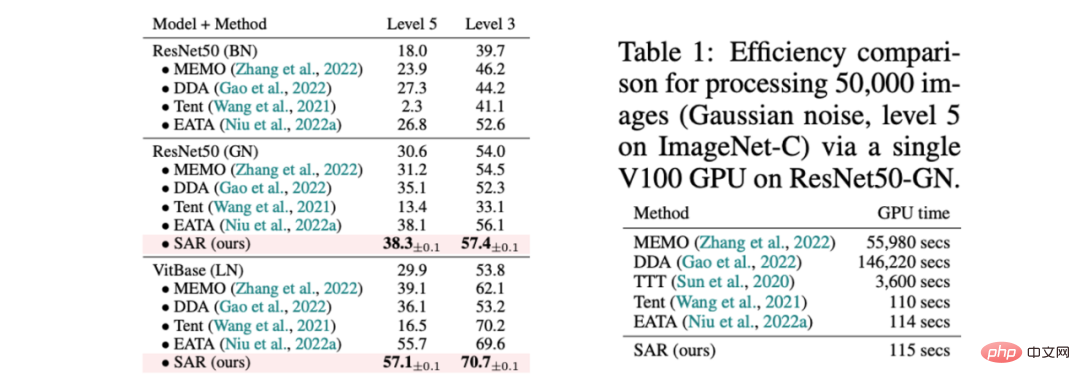
Tableau 1 Comparaison des performances entre SAR et méthodes existantes dans des scénarios mixtes de 15 types de dommages dans ImageNet-C, correspondant au scénario dynamique (a) et comparaison d'efficacité avec les méthodes existantes 有 Tableau 2 SAR et la méthode existante sur la comparaison des performances dans le scénario dans ImageNet-C, correspondant à la scène dynamique (B)
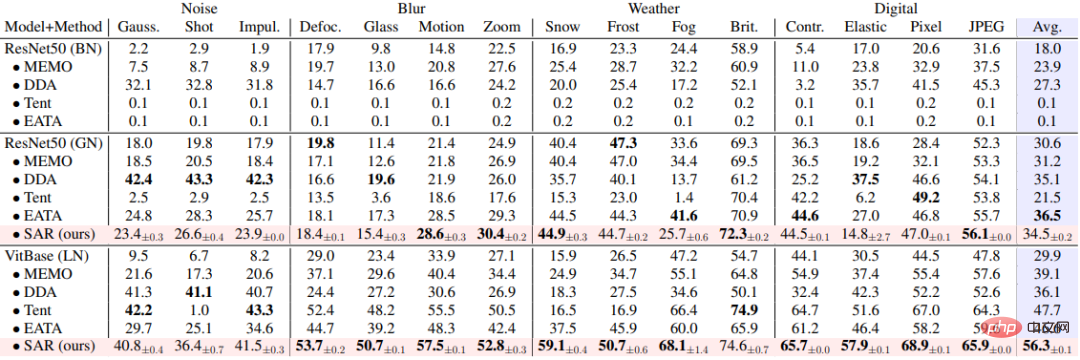
Tableau 3 Comparaison des performances entre SAR et les méthodes existantes dans Scénario de changement de répartition des classes non équilibrées en ligne sur ImageNet-C, correspondant au scénario dynamique (c)
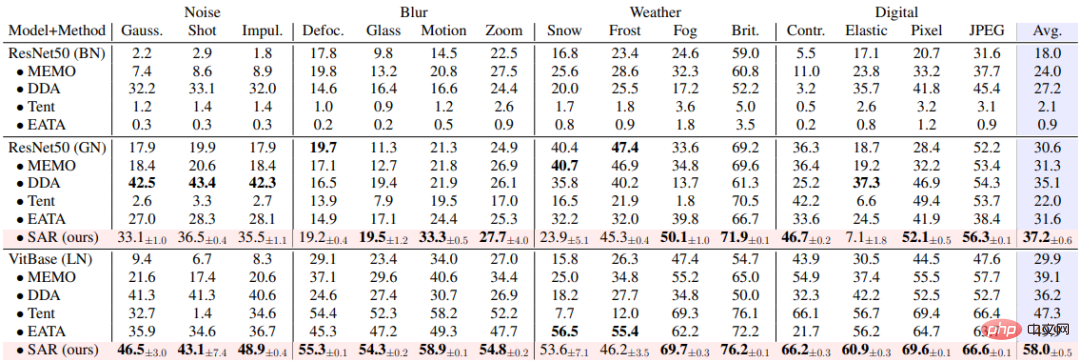
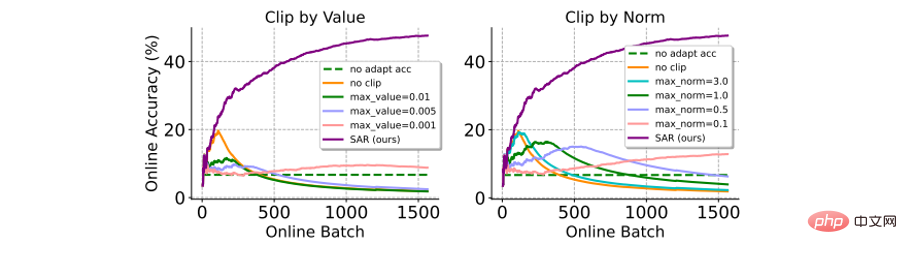
et méthode de découpage en dégradé Comparaison : Le découpage en dégradé est une méthode simple et directe pour éviter que des dégradés importants n'affectent les mises à jour du modèle (ou même provoquent un effondrement). Voici une comparaison avec deux variantes de dégradé (c'est-à-dire : par valeur ou par norme). Comme le montre la figure ci-dessous, l'écrêtage du gradient est très sensible à la sélection du seuil d'écrêtage du gradient δ. Un δ plus petit équivaut au résultat de la non-mise à jour du modèle, et un δ plus grand est difficile à éviter l'effondrement du modèle. En revanche, le SAR ne nécessite pas de processus de filtrage d’hyperparamètres compliqué et fonctionne nettement mieux que l’écrêtage par gradient.
Figure 7 Comparaison des performances avec la méthode d'écrêtage par gradient dans le scénario de changement de distribution d'étiquettes déséquilibrées en ligne sur ImageNet-C (shot nosine, niveau 5). La précision est calculée en ligne sur la base de tous les échantillons de tests précédents
: Comme le montre le tableau ci-dessous, les différents modules de SAR travaillent ensemble pour améliorer efficacement le test en mode ouvert dynamique. scénarios de stabilité adaptative du modèle temporel.
Tableau 4 Expérience d'ablation SAR sur ImageNet-C (niveau 5) dans un scénario de changement de distribution d'étiquettes déséquilibrées en ligne
Visualisation de la netteté de la surface de perte : Le résultat de la visualisation de la fonction de perte en ajoutant une perturbation au poids du modèle est présenté dans la figure ci-dessous. Parmi eux, le SAR a une zone plus grande (zone bleu foncé) dans le contour de perte le plus faible que Tent, ce qui indique que la solution obtenue par SAR est plus plate, plus robuste au bruit/gradients plus importants et a une capacité anti-interférence plus forte.
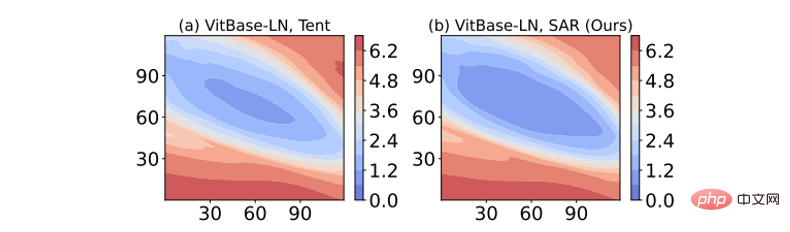
Figure 8 Visualisation de la surface de perte d'entropie
Conclusion
Cet article est dédié à la résolution du problème de l'instabilité adaptative lors des tests de modèles en ligne dans des scénarios ouverts dynamiques. À cette fin, cet article analyse d’abord les raisons pour lesquelles les méthodes existantes échouent dans des scénarios dynamiques réels dans une perspective unifiée, et conçoit des expériences complètes pour effectuer une vérification approfondie. Sur la base de ces analyses, cet article propose enfin une méthode de minimisation de l'entropie au temps de test fiable et sensible à la netteté, qui permet une adaptation stable et efficace du temps de test en ligne du modèle en supprimant l'impact de certains échantillons de test avec des gradients/bruit importants sur les mises à jour du modèle. .
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

