Maison >Périphériques technologiques >IA >La précision de GPT-3 dans la résolution de problèmes mathématiques est passée à 92,5 % ! Microsoft propose MathPrompter pour créer des modèles de langage « scientifiques » sans réglage fin
La précision de GPT-3 dans la résolution de problèmes mathématiques est passée à 92,5 % ! Microsoft propose MathPrompter pour créer des modèles de langage « scientifiques » sans réglage fin
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-04-12 21:25:011897parcourir
Le défaut le plus critiqué des grands modèles de langage, outre de graves absurdités, est probablement leur « incapacité à faire des mathématiques ».
Par exemple, pour un problème mathématique complexe qui nécessite un raisonnement en plusieurs étapes, le modèle de langage est généralement incapable de donner la bonne réponse. Même avec la bénédiction de la technologie de la « chaîne de pensée », des erreurs se produisent souvent. dans les étapes intermédiaires.
Contrairement aux tâches de compréhension du langage naturel dans les arts libéraux, les questions mathématiques n'ont souvent qu'une seule bonne réponse, avec une gamme de réponses moins ouverte, ce qui rend la tâche de génération de solutions précises plus difficile pour les grands modèles de langage.
De plus, lorsqu'il s'agit de problèmes mathématiques, les modèles de langage existants ne fournissent généralement pas de confiance dans leurs réponses, laissant les utilisateurs incapables de juger de la crédibilité des réponses générées.
Afin de résoudre ce problème, Microsoft Research a proposé la technologie MathPrompter, qui peut améliorer les performances du LLM sur les problèmes arithmétiques tout en augmentant son recours à la prédiction.
Lien papier : https://arxiv.org/abs/2303.05398
MathPrompter utilise la technologie d'invite de chaîne de réflexion Zero-shot pour générer plusieurs expressions algébriques ou fonctions Python afin de résoudre les mêmes problèmes mathématiques de différentes manières. , améliorant ainsi la crédibilité des résultats.
Par rapport à d'autres méthodes CoT basées sur des indices, MathPrompter vérifie également la validité des étapes intermédiaires.
Basé sur le paramètre GPT 175B, en utilisant la méthode MathPrompter pour augmenter la précision de l'ensemble de données MultiArith de 78,7 % à 92,5 % !
Prompt spécialisé en mathématiques
Ces dernières années, le développement du traitement du langage naturel est en grande partie dû à l'expansion continue de l'échelle des grands modèles de langage (LLM), qui ont démontré d'étonnantes capacités de tir zéro et peu de tirs a également contribué au développement de la technologie d'invite. Les utilisateurs n'ont besoin que de saisir quelques échantillons simples dans LLM pour prédire de nouvelles tâches.
prompt peut être considéré comme assez efficace pour les tâches en une seule étape, mais dans les tâches nécessitant un raisonnement en plusieurs étapes, les performances de la technologie prompte sont encore insuffisantes.
Lorsque les humains résolvent un problème complexe, ils le décomposent et tentent de le résoudre étape par étape. La technologie d'invite « Chaîne de pensée » (CoT) étend cette intuition aux LLM, dans une série de tâches qui nécessitent un raisonnement. Des améliorations des performances ont été obtenues dans les tâches PNL.
Cet article étudie principalement la méthode Zero-shot-CoT « pour résoudre des tâches de raisonnement mathématique ». Des travaux antérieurs ont permis d'améliorer considérablement la précision de l'ensemble de données MultiArith, de 17,7 % à 78,7 %. :
1. Bien que la chaîne de réflexion suivie par le modèle améliore les résultats, il ne vérifie pas l'efficacité de chaque étape suivie par les invites de la chaîne de réflexion
2, ne fournit pas de confiance pour les résultats de prédiction du LLM ; .
MathPrompter
Pour combler ces lacunes dans une certaine mesure, les chercheurs s'inspirent de « la façon dont les humains résolvent les problèmes mathématiques », décomposant les problèmes complexes en procédures plus simples en plusieurs étapes et utilisant plusieurs méthodes pour résoudre chaque problème. la méthode en une seule étape.
Étant donné que LLM est un modèle génératif, il devient très délicat de garantir que les réponses générées sont exactes, en particulier pour les tâches de raisonnement mathématique.
Les chercheurs ont observé le processus par lequel les élèves résolvent des problèmes arithmétiques et ont résumé plusieurs étapes suivies par les élèves pour vérifier leurs solutions :
Conformité aux résultats connus En comparant la solution avec les résultats connus, vous pouvez évaluer son exactitude et effectuer les ajustements nécessaires ; lorsque le problème est un problème standard avec une solution mature, cela est particulièrement utile. La
Multi-vérification, en abordant le problème sous plusieurs angles et en comparant les résultats, permet de confirmer l'efficacité de la solution et garantit qu'elle est à la fois raisonnable et précise.
Vérification croisée, le processus de résolution du problème est aussi nécessaire que la réponse finale ; vérifier l'exactitude des étapes intermédiaires du processus peut fournir une compréhension claire du processus de réflexion derrière la solution.
La vérification informatique, l'utilisation d'une calculatrice ou d'un ordinateur pour effectuer des calculs arithmétiques peut aider à vérifier l'exactitude de la réponse finale
Plus précisément, étant donné une question Q,

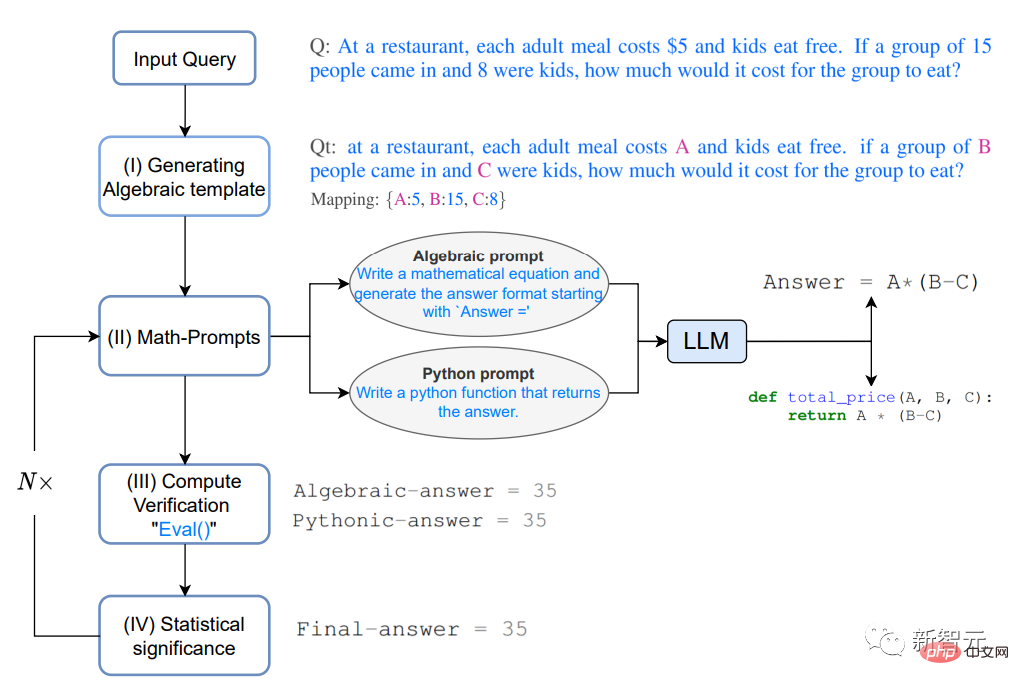
Dans un restaurant, le prix de chaque repas adulte est de 5 $ et les enfants mangent gratuitement. Si 15 personnes entrent et que 8 d’entre elles sont des enfants, combien cela coûte-t-il de manger pour ce groupe de personnes ?
1. Génération d'un modèle algébrique
Convertissez d'abord le problème sous forme algébrique, en utilisant le mappage clé-valeur pour remplacer les éléments numériques par des variables, puis obtenez le problème modifié Qt

2. Invites mathématiques
Sur la base de l'intuition fournie par le processus de réflexion ci-dessus de validation multiple et de vérification croisée, deux méthodes différentes sont utilisées pour générer des solutions d'analyse pour Qt, à savoir algébriquement et Pythoniquement, LLM reçoit les astuces suivantes pour générer un contexte supplémentaire pour Qt.

L'invite peut être "Dériver une expression algébrique" ou "Écrire une fonction Python"
Le modèle LLM peut générer l'expression suivante après avoir répondu à l'invite.

Le plan d'analyse généré ci-dessus fournit aux utilisateurs des conseils sur le "processus de réflexion intermédiaire" du LLM. L'ajout de conseils supplémentaires peut améliorer l'exactitude et la cohérence des résultats, ce qui à son tour améliorera MathPrompter pour générer des résultats plus précis et plus précis. Capacité à apporter des solutions efficaces.
3. Vérification du calcul
Utilisez plusieurs cartes clé-valeur aléatoires de variables d'entrée dans Qt pour évaluer les expressions générées à l'étape précédente et utilisez la méthode eval() de Python pour évaluer ces expressions. une évaluation.
Comparez ensuite les résultats pour voir si vous pouvez trouver un consensus dans la réponse, ce qui peut également fournir une plus grande confiance dans le fait que la réponse est correcte et fiable.

Une fois l'expression convenue sur la sortie, utilisez les valeurs des variables dans l'entrée Q pour calculer la réponse finale.
4. Signification statistique
Pour garantir un consensus dans la sortie de diverses expressions, répétez les étapes 2 et 3 environ 5 fois dans l'expérience et signalez l'occurrence observée des valeurs de réponse les plus fréquentes.
En l'absence de consensus clair, répétez les étapes 2, 3 et 4.
Résultats expérimentaux
Évaluez MathPrompter sur l'ensemble de données MultiArith. Les questions mathématiques qu'il contient sont spécifiquement utilisées pour tester la capacité du modèle d'apprentissage automatique à effectuer des opérations et des raisonnements arithmétiques complexes. raisonnement logique pour réussir à résoudre.
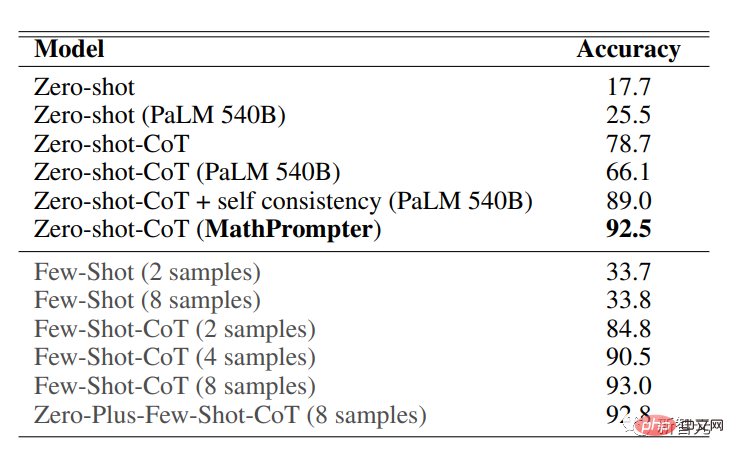
Les résultats de précision sur l'ensemble de données MultiArith montrent que MathPrompter surpasse toutes les lignes de base Zero-shot et Zero-shot-CoT, augmentant la précision de 78,7% à 92,5%
On peut voir que les performances du modèle MathPrompter basé sur le paramètre 175B GPT3 DaVinci sont comparables au modèle de paramètre 540B et à la méthode Few-shot-CoT de SOTA.

Comme vous pouvez le voir dans le tableau ci-dessus, la conception de MathPrompter peut compenser des problèmes tels que "les réponses générées ont parfois une différence d'un cran", qui peuvent être évitées en exécutant le modèle plusieurs fois. et rendre compte des résultats du consensus.
De plus, le problème selon lequel l'étape d'inférence peut être trop longue peut être résolu par des méthodes pythoniques ou algébriques, qui nécessitent généralement moins de jetons
De plus, l'étape d'inférence peut être correcte, mais le résultat final du calcul n'est pas incorrect, MathPrompter résout ce problème en utilisant la fonction de méthode eval() de Python.
Dans la plupart des cas, MathPrompter peut générer des réponses intermédiaires et finales correctes, mais il existe quelques cas, comme la dernière question du tableau, où les résultats algébriques et pythoniques sont cohérents, mais il y a des erreurs.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

