18 images pour comprendre intuitivement les réseaux de neurones, les variétés et la topologie

À ce jour, l’un des gros soucis concernant les réseaux de neurones est qu’ils sont des boîtes noires difficiles à expliquer. Cet article comprend principalement théoriquement pourquoi les réseaux de neurones sont si efficaces dans la reconnaissance et la classification des formes. Son essence est de déformer et de déformer l'entrée originale à travers des couches de transformation affine et de transformation non linéaire jusqu'à ce qu'elle puisse être facilement distinguée en différentes catégories. En fait, l’algorithme de rétro-propagation (BP) affine en permanence l’effet de distorsion en fonction des données d’entraînement.

Depuis une dizaine d’années, les réseaux de neurones profonds ont obtenu des résultats révolutionnaires dans des domaines tels que la vision par ordinateur, suscitant un grand intérêt et une grande attention.

Cependant, certaines personnes s’en inquiètent encore. L’une des raisons est qu’un réseau de neurones est une boîte noire : si un réseau de neurones est bien entraîné, des résultats de haute qualité peuvent être obtenus, mais il est difficile de comprendre son fonctionnement. En cas de dysfonctionnement d’un réseau neuronal, il peut être difficile d’identifier le problème.

Bien qu'il soit difficile de comprendre les réseaux de neurones profonds dans leur ensemble, vous pouvez commencer par des réseaux de neurones profonds de faible dimension, c'est-à-dire des réseaux avec seulement quelques neurones dans chaque couche, qui sont beaucoup plus faciles à comprendre. Nous pouvons comprendre le comportement et la formation des réseaux de neurones profonds de basse dimension grâce à des méthodes de visualisation. Les méthodes de visualisation nous permettent de comprendre le comportement des réseaux de neurones de manière plus intuitive et d'observer le lien entre les réseaux de neurones et la topologie.

Je parlerai ensuite de beaucoup de choses intéressantes, y compris la limite inférieure de la complexité d'un réseau neuronal capable de classer un ensemble de données spécifique.

1. Un exemple simple

Commençons par un ensemble de données très simple. Dans la figure ci-dessous, deux courbes sur le plan sont composées d'innombrables points. Le réseau de neurones va tenter de distinguer à quelle ligne appartiennent ces points.

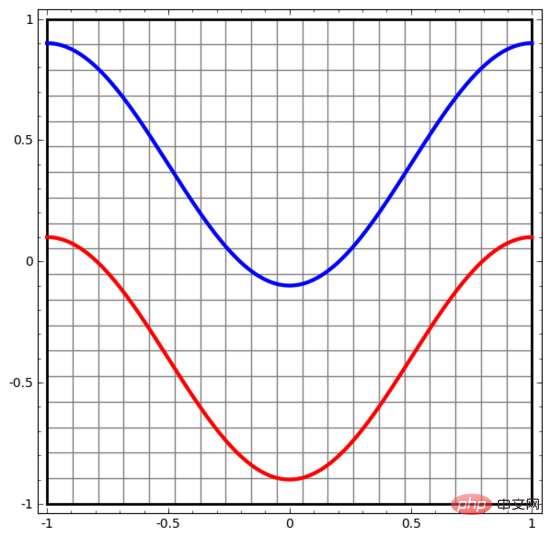
Le moyen le plus simple d'observer le comportement d'un réseau de neurones (ou de tout algorithme de classification) est de voir comment il classe chaque point de données.

Nous commençons par le réseau neuronal le plus simple, qui n'a qu'une seule couche d'entrée et une seule couche de sortie. Un tel réseau neuronal sépare simplement deux types de points de données par une ligne droite.

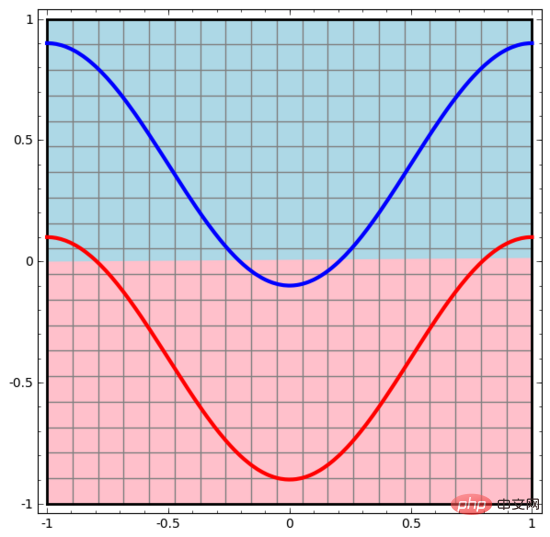
Un tel réseau de neurones est trop simple et grossier. Les réseaux de neurones modernes comportent souvent plusieurs couches entre les couches d’entrée et de sortie, appelées couches cachées. Même le réseau neuronal moderne le plus simple possède au moins une couche cachée.

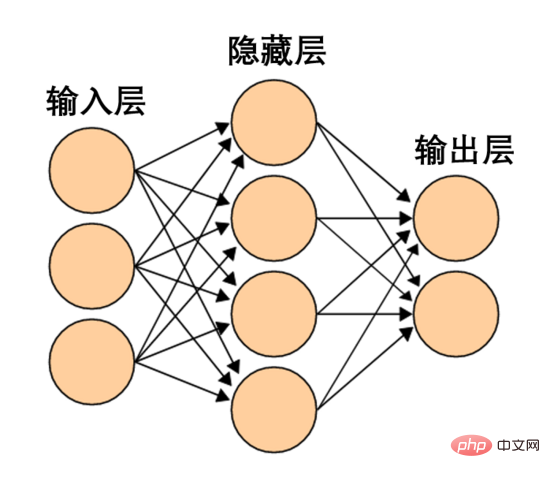
Un réseau de neurones simple, source d'image Wikipédia

De même, nous observons ce que fait le réseau de neurones pour chaque point de données. Comme on peut le constater, ce réseau neuronal utilise une courbe au lieu d’une ligne droite pour séparer les points de données. Évidemment, les courbes sont plus complexes que les lignes droites.

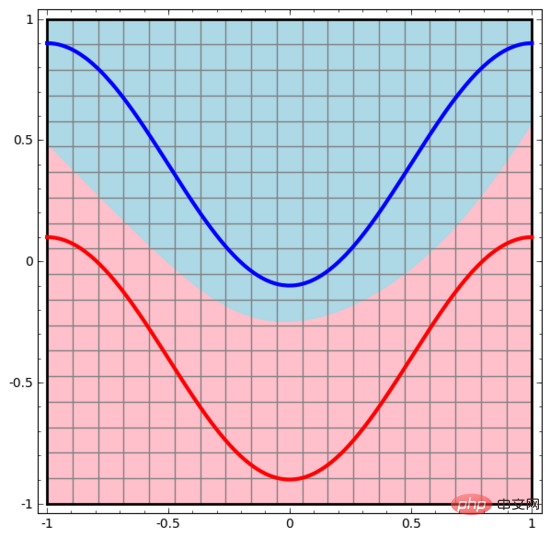
Chaque couche du réseau neuronal utilise une nouvelle représentation pour représenter les données. Nous pouvons observer comment les données sont transformées en nouvelles représentations et comment le réseau neuronal les classe. Dans la dernière couche de représentation, le réseau neuronal trace une ligne entre les deux types de données (ou un hyperplan si en dimensions supérieures).

Dans la visualisation précédente, nous avons vu la représentation originale des données. Vous pouvez y penser comme à quoi ressemblent les données dans la « couche d’entrée ». Voyons maintenant à quoi ressemblent les données après leur transformation. Vous pouvez les considérer comme ce à quoi ressemblent les données dans la « couche cachée ».

Chaque dimension des données correspond à l'activation d'un neurone dans la couche du réseau neuronal.

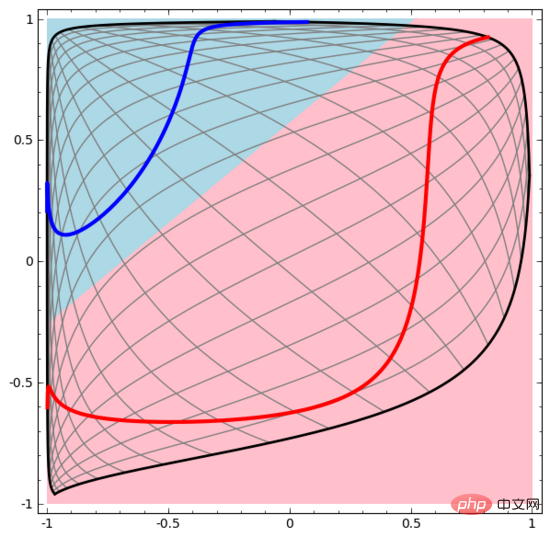
La couche cachée utilise la méthode ci-dessus pour représenter les données, de sorte que les données puissent être séparées par une ligne droite (c'est-à-dire linéairement séparables)

2. Visualisation continue des couches

Dans la méthode du section précédente, chaque couche du réseau neuronal représente les données dans différentes représentations. De cette manière, les représentations de chaque couche sont discrètes et non continues.

Cela crée des difficultés dans notre compréhension. Comment passer d'une représentation à une autre ? Heureusement, les caractéristiques de la couche réseau neuronal permettent de comprendre très facilement cet aspect.

Il existe différentes couches dans les réseaux de neurones. Ci-dessous, nous discuterons de la couche tanh comme exemple spécifique. Une couche tanh, comprenant :

• Utilisez la matrice "poids" W pour la transformation linéaire
• Utilisez le vecteur b pour la traduction
• Utilisez tanh pour représenter point par point

On peut la considérer comme une transformation continue, comme suit :

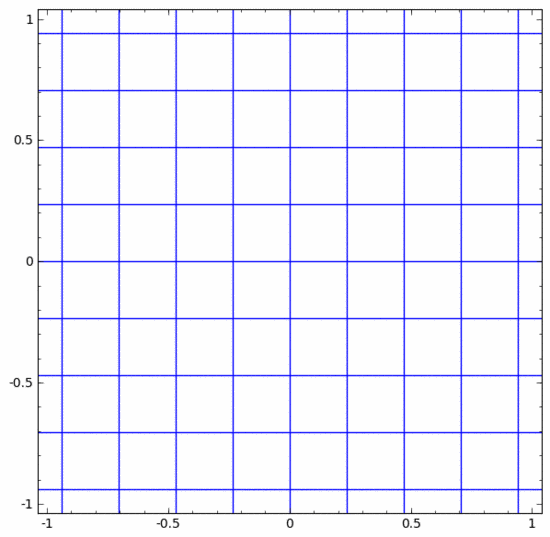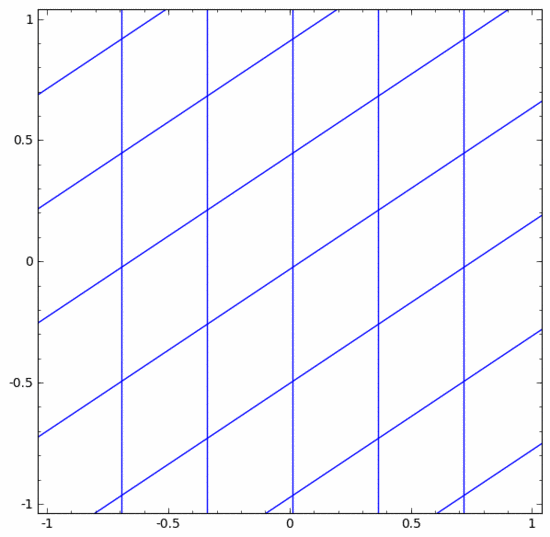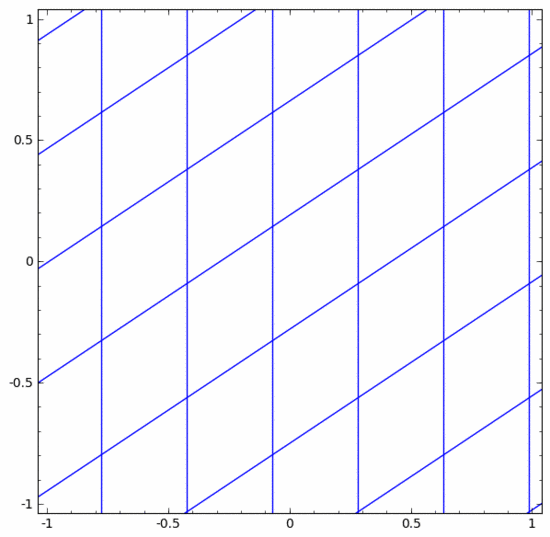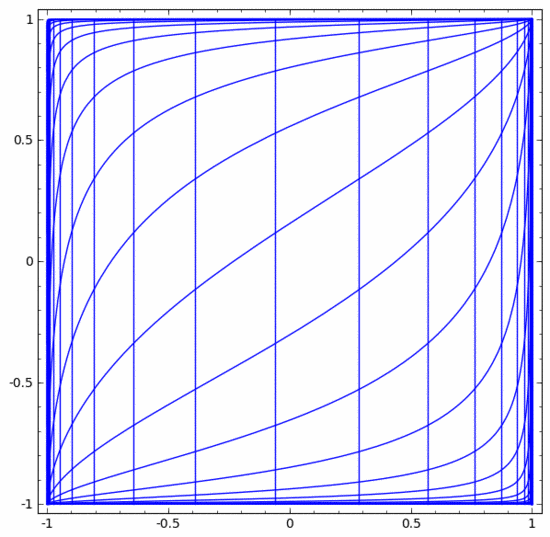
Les autres couches standards sont à peu près les mêmes, consistant en une application ponctuelle de transformations affines et de fonctions d'activation monotones.

Nous pouvons utiliser cette méthode pour comprendre des réseaux de neurones plus complexes. Par exemple, le réseau neuronal ci-dessous utilise quatre couches cachées pour classer deux spirales légèrement entrelacées. On voit que pour classer les données, la représentation des données est continuellement transformée. Les deux spirales sont initialement enchevêtrées, mais elles peuvent éventuellement être séparées par une ligne droite (linéairement séparable).

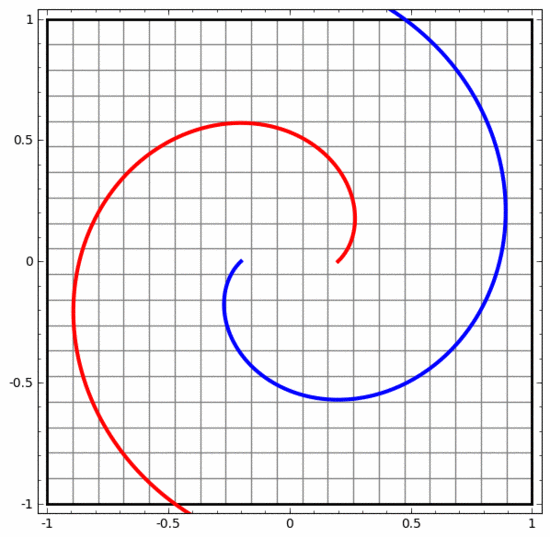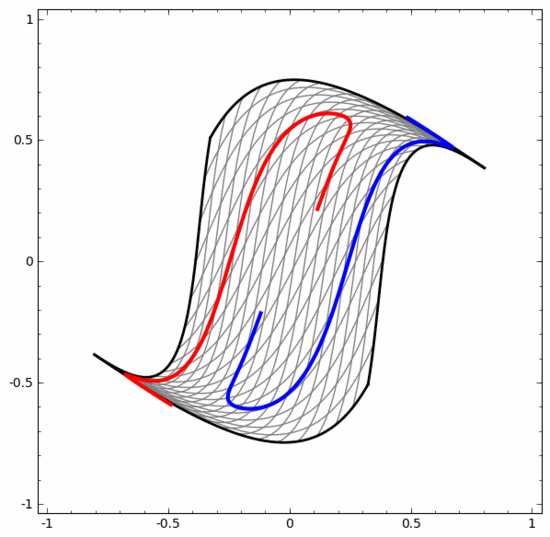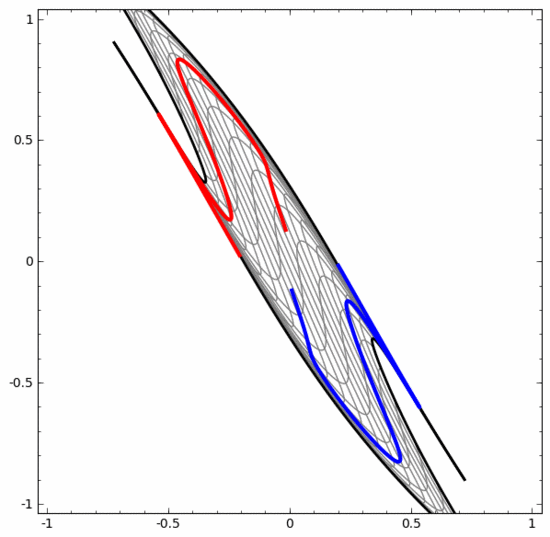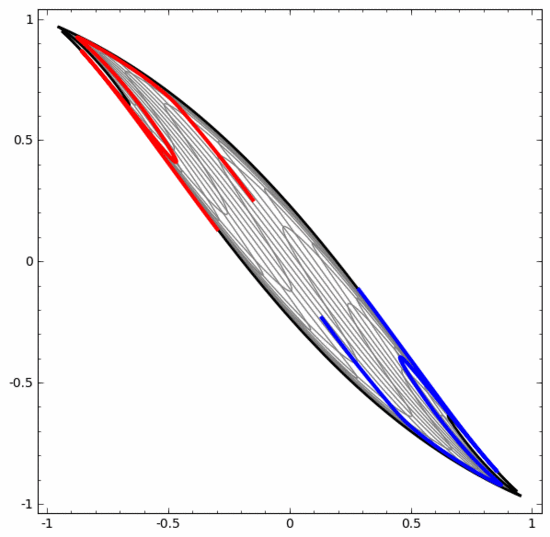
D'un autre côté, bien que le réseau neuronal ci-dessous utilise également plusieurs couches cachées, il ne peut pas diviser deux spirales plus profondément entrelacées.

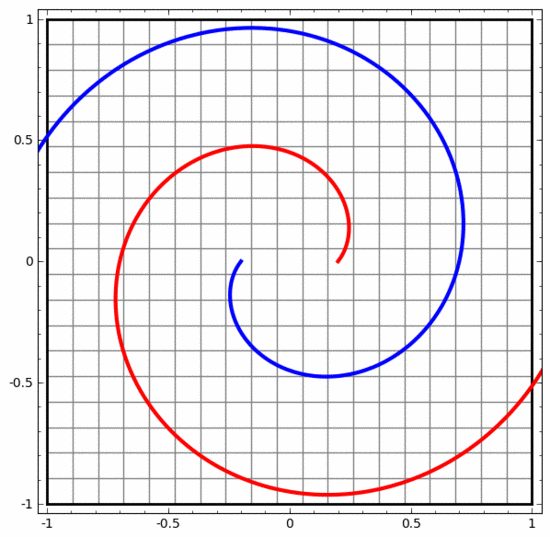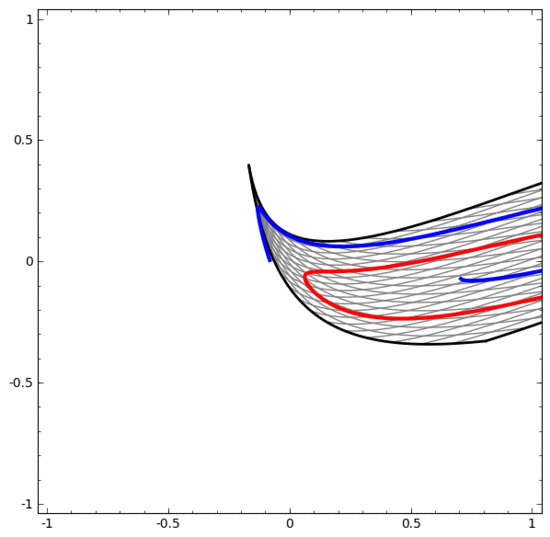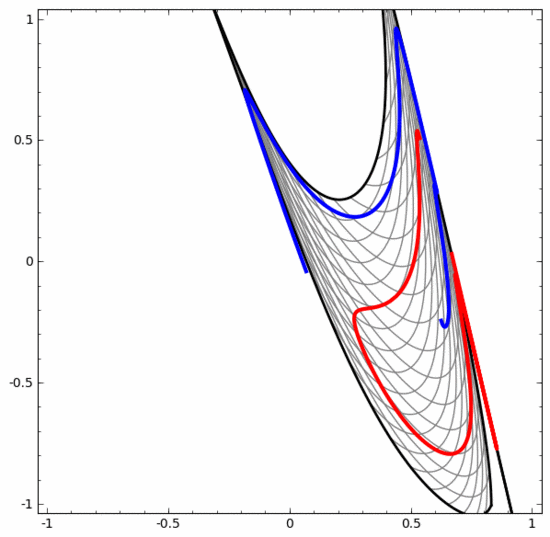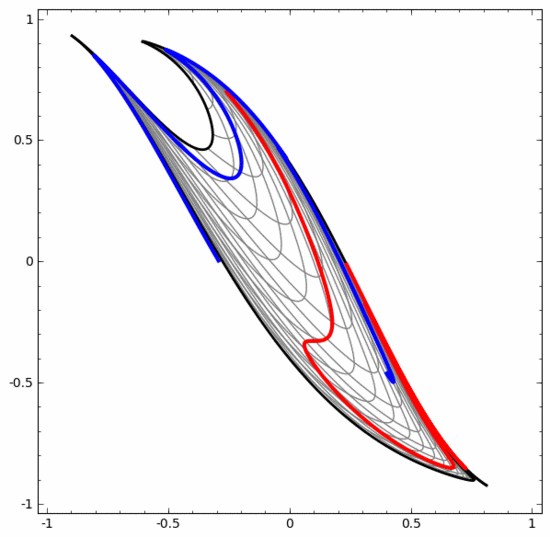
Il convient de souligner clairement que les deux tâches de classification en spirale ci-dessus présentent certains défis car nous n'utilisons actuellement que des réseaux neuronaux de faible dimension. Tout serait beaucoup plus simple si nous utilisions un réseau neuronal plus large.

(Andrej Karpathy a fait une bonne démo basée sur ConvnetJS, qui permet aux gens d'explorer le réseau neuronal de manière interactive grâce à ce type de formation visuelle.)

3 Topologie de la couche tanh

Chaque couche du réseau neuronal s'étendra. et réduit l'espace, mais il ne le cisaille pas, ne le divise pas et ne le plie pas. Intuitivement, les réseaux de neurones ne détruisent pas les propriétés topologiques des données. Par exemple, si un ensemble de données est continu, alors sa représentation transformée sera également continue (et vice versa).

Des transformations comme celle-ci qui n'affectent pas les propriétés topologiques sont appelées homéomorphismes. Formellement, ce sont des bijections de fonctions continues bidirectionnelles.

Théorème : Si la matrice de poids W est non singulière et qu'une couche du réseau neuronal a N entrées et N sorties, alors la cartographie de cette couche est homéomorphe (pour un domaine et une plage de valeurs spécifiques).

Preuve : Allons-y étape par étape :

1. Supposons que W ait un déterminant non nul. C'est alors une fonction linéaire bilinéaire avec un inverse linéaire. Les fonctions linéaires sont continues. Ensuite, la transformation telle que « multiplier par W » est l'homéomorphisme ;

2. La transformation « traduction » est l'homéomorphisme

3. tanh (également sigmoïde et softplus, mais n'incluant pas ReLU) est une fonction continue. (pour un domaine et une plage particuliers), ce sont des bijections, et leur application ponctuelle est l'homéomorphisme.

Par conséquent, s'il existe un déterminant non nul de W, cette couche de réseau neuronal est homéomorphe.

Si nous combinons ces couches au hasard, ce résultat est toujours valable.

4. Topologie et classification

Regardons un ensemble de données bidimensionnelles, qui contient deux types de données A et B :

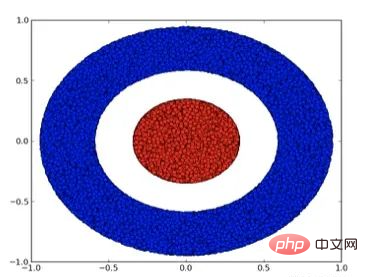
A est rouge, B est bleu

Explication : Pour comprendre ceci Pour qu'un ensemble de données soit classé, un réseau de neurones (quelle que soit sa profondeur) doit avoir une couche contenant 3 unités cachées ou plus.

Comme mentionné précédemment, utiliser des unités sigmoïdes ou des couches softmax pour la classification équivaut à trouver un hyperplan (dans ce cas, une ligne droite) dans la représentation de la dernière couche pour séparer A et B. Avec seulement deux unités cachées, le réseau neuronal est topologiquement incapable de séparer les données de cette manière et ne peut donc pas classer l'ensemble de données ci-dessus.

Dans la visualisation ci-dessous, la couche cachée transforme la représentation des données, avec des lignes droites comme lignes de séparation. On peut voir que la ligne de démarcation continue de tourner et de se déplacer, mais elle n'est jamais capable de bien séparer les deux types de données A et B.

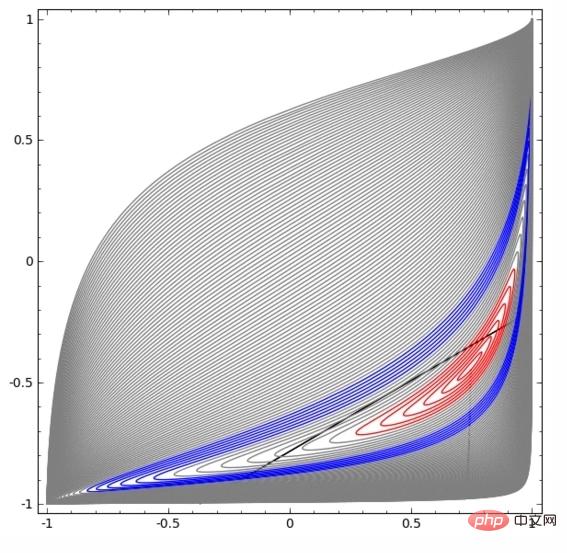
Peu importe à quel point un réseau neuronal est bien formé, il ne peut pas bien accomplir la tâche de classification

En fin de compte, il peut à peine atteindre un minimum local et atteindre une précision de classification de 80 %.

L'exemple ci-dessus n'a qu'une seule couche cachée, et comme il n'y a que deux unités cachées, il ne pourra de toute façon pas être classé.

Preuve : S'il n'y a que deux unités cachées, soit la transformation de cette couche est homéomorphe, soit la matrice de poids de la couche a un déterminant 0. S'il s'agit d'un homéomorphisme, A est toujours entouré de B, et A et B ne peuvent pas être séparés par une ligne droite. S'il existe un déterminant de 0, alors l'ensemble de données sera réduit sur un axe. Étant donné que A est entouré par B, le pliage de A sur n’importe quel axe entraînera le mélange de certains points de données A avec B, rendant impossible la distinction de A de B.

Mais si on ajoute une troisième unité cachée, le problème est résolu. A ce moment, le réseau de neurones peut convertir les données dans la représentation suivante :

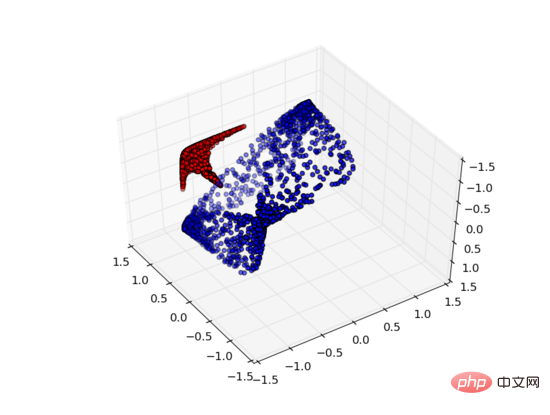
A ce moment, un hyperplan peut être utilisé pour séparer A et B.

Pour mieux expliquer son principe, voici un exemple d'ensemble de données unidimensionnel plus simple :

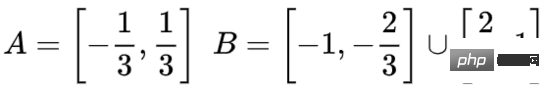
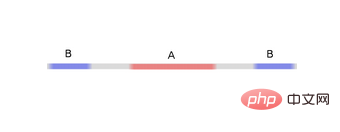
Pour classer cet ensemble de données, vous devez utiliser une unité cachée composée de deux ou plusieurs couches d'unités cachées. Si vous utilisez deux unités cachées, vous pouvez utiliser une belle courbe pour représenter les données, de sorte que vous puissiez utiliser une ligne droite pour séparer A et B :

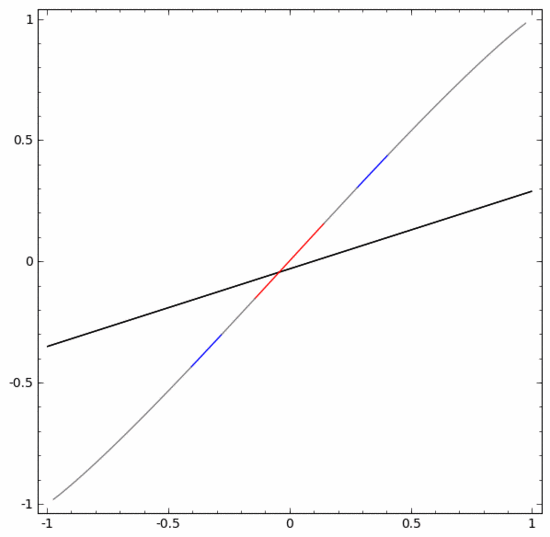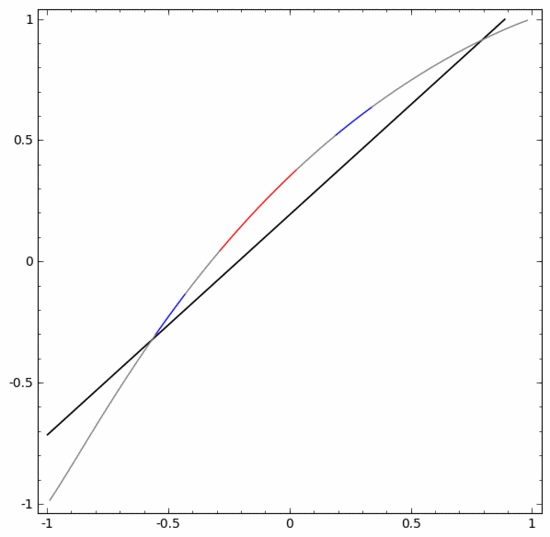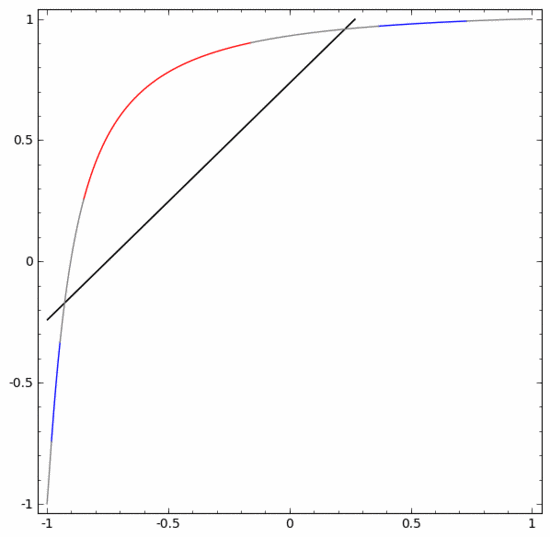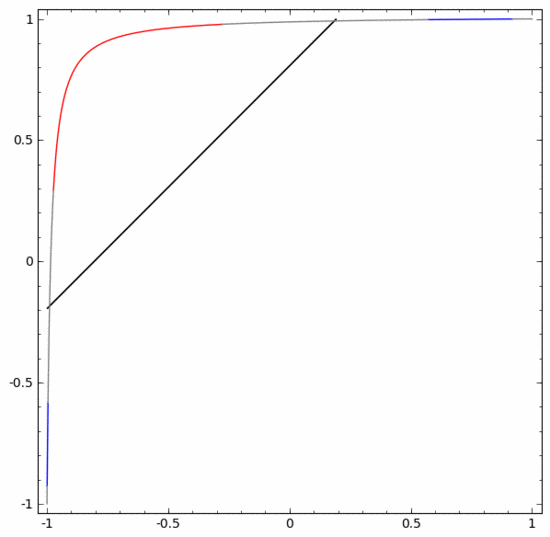
Comment cela se fait-il ? Lorsque , l'une des unités cachées est activée ; lorsque 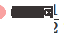, l'autre unité cachée est activée. Lorsque l'unité cachée précédente est activée et que l'unité cachée suivante n'est pas activée, on peut juger qu'il s'agit d'un point de données appartenant à A.

5. Hypothèse multiple

L'hypothèse multiple est-elle significative pour le traitement d'ensembles de données du monde réel (tels que les données d'image) ? Je pense que c'est logique.

L'hypothèse de la variété signifie que les données naturelles forment une variété de faible dimension dans son espace d'intégration. Cette hypothèse a un soutien théorique et expérimental. Si vous croyez en l’hypothèse de la variété, alors la tâche d’un algorithme de classification se résume à séparer un ensemble de variétés intriquées.

Dans l'exemple précédent, une classe entourait complètement l'autre classe. Cependant, dans les données du monde réel, il est peu probable que la variété d’images de chien soit complètement entourée par la variété d’images de chat. Cependant, d’autres situations topologiques plus raisonnables peuvent encore poser des problèmes, comme nous le verrons dans la section suivante.

6. Liens et homotopie

Maintenant, je vais parler d'un autre ensemble de données intéressant : deux tores liés (tori), A et B.

Semblable à la situation d'ensemble de données dont nous avons parlé précédemment, vous ne pouvez pas séparer un ensemble de données à n dimensions sans utiliser la dimension n+1 (la dimension n+1 est la 4ème dimension dans cet exemple).

Le problème du lien appartient à la théorie des nœuds en topologie. Parfois, lorsque nous voyons un lien, nous ne pouvons pas immédiatement dire s'il s'agit d'un lien rompu (dissocier signifie que même s'ils sont enchevêtrés les uns dans les autres, ils peuvent être séparés par une déformation continue).

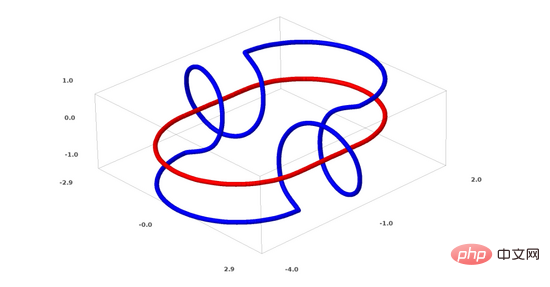
Un lien rompu plus simple

Si un réseau de neurones avec seulement 3 unités cachées dans la couche cachée peut classer un ensemble de données, alors cet ensemble de données est un lien rompu (le problème est le suivant : théoriquement, tous les liens rompus peuvent-ils être classé par un réseau de neurones avec seulement 3 unités cachées ?

Du point de vue de la théorie des nœuds, la visualisation continue des représentations de données produites par les réseaux de neurones n'est pas seulement une belle animation, mais aussi un processus de dénouement des liens. En topologie, on appelle cela l'isotopie ambiante entre le lien d'origine et le lien séparé.

L'homomorphisme environnant entre la variété A et la variété B est une fonction continue :

Chacune est un homéomorphisme de X. est la fonction caractéristique, mappant A à B. Autrement dit, passer constamment du mappage de A à lui-même au mappage de A à B.

Théorème : Si les trois conditions suivantes sont remplies en même temps : (1) W est non singulier ; (2) l'ordre des neurones dans la couche cachée peut être organisé manuellement (3) le nombre d'unités cachées est plus grand ; supérieur à 1, alors l'entrée du réseau neuronal et le réseau neuronal Il existe une trace enveloppante entre les représentations produites par la couche réseau.

Preuve : On y va aussi étape par étape :

1 La partie la plus difficile est la transformation linéaire. Pour réaliser une transformation linéaire, nous avons besoin que W ait un déterminant positif. Notre principe est que le déterminant est non nul, et si le déterminant est négatif, nous pouvons le transformer en positif en échangeant deux neurones cachés. L'espace de la matrice déterminante positive est connecté au chemin, il y a donc 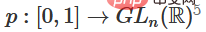, donc 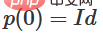, 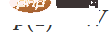. Avec la fonction 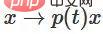, nous pouvons faire passer continuellement la fonction propre à la transformation W, en multipliant x par la matrice de la transition continue en chaque point au temps t.

2. Vous pouvez passer de la fonction caractéristique à la traduction b via la fonction .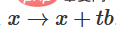

3. Vous pouvez passer de la fonction caractéristique à l'application point par point grâce à la fonction .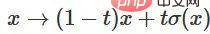

Je suppose que quelqu'un pourrait être intéressé par la question suivante : peut-on développer un programme capable de découvrir automatiquement une telle isotopie ambiante, et pouvant également prouver automatiquement l'équivalence de certains liens différents ou l'équivalence de certains liens ? Je veux également savoir si les réseaux de neurones peuvent battre la technologie SOTA actuelle à cet égard.

Bien que la forme de liaison dont nous parlons maintenant n'apparaîtra probablement pas dans les données du monde réel, il peut y avoir des généralisations de dimension supérieure dans les données du monde réel.

Les liens et les nœuds sont tous deux des variétés unidimensionnelles, mais 4 dimensions sont nécessaires pour les séparer. De même, pour séparer une variété à n dimensions, un espace de dimension supérieure est nécessaire. Toutes les variétés à n dimensions peuvent être séparées en 2n+2 dimensions.

7. Une méthode simple

Pour les réseaux de neurones, la méthode la plus simple consiste à séparer directement les variétés entrelacées et à rendre ces parties enchevêtrées aussi fines que possible. Bien que ce ne soit pas la solution fondamentale que nous recherchons, elle peut atteindre une précision de classification relativement élevée et un minimum local relativement idéal.

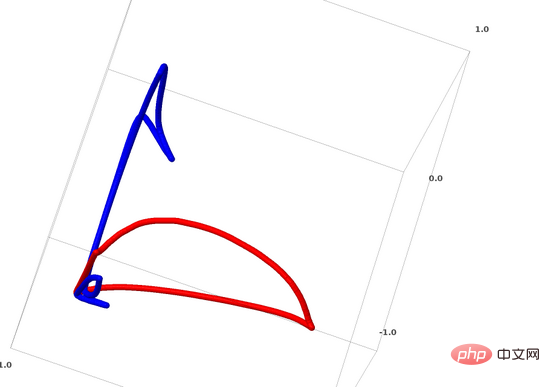
Cette approche aboutit à des dérivées très élevées dans la zone que vous essayez d'étirer. Pour résoudre ce problème, vous devez utiliser une pénalité de retrait, qui pénalise la dérivée de la couche de points de données.

Les minima locaux ne sont pas utiles pour résoudre des problèmes topologiques, mais les problèmes topologiques peuvent fournir de bonnes idées pour explorer et résoudre les problèmes ci-dessus.

D'un autre côté, si nous ne nous soucions que d'obtenir de bons résultats de classification, est-ce un problème pour nous si une petite partie du collecteur est empêtrée dans un autre collecteur ? Si nous nous soucions uniquement des résultats de la classification, cela ne semble pas poser de problème.

(Mon intuition est que prendre des raccourcis comme celui-ci n'est pas bon et peut facilement conduire à une impasse. En particulier, dans les problèmes d'optimisation, rechercher un minimum local ne résout pas vraiment le problème, et si vous choisissez un minimum local qui le fait ne résoudra pas vraiment le problème. La solution ne parviendra finalement pas à obtenir de bonnes performances)

8. Choisir une couche de réseau neuronal plus adaptée à la manipulation multiple ?

Je pense que les couches de réseaux neuronaux standard ne sont pas adaptées à la manipulation de variétés car elles utilisent des transformations affines et des fonctions d'activation ponctuelles.

Peut-être pouvons-nous utiliser une couche de réseau neuronal complètement différente ?

Une idée qui me vient à l'esprit est, d'abord, de laisser le réseau de neurones apprendre un champ vectoriel dont la direction est la direction dans laquelle nous voulons déplacer la variété :

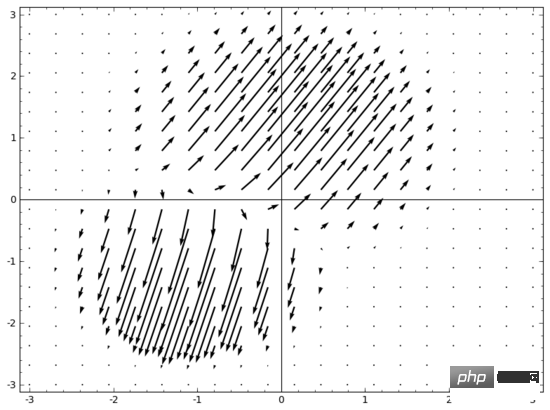
, puis de déformer l'espace en fonction de ceci :

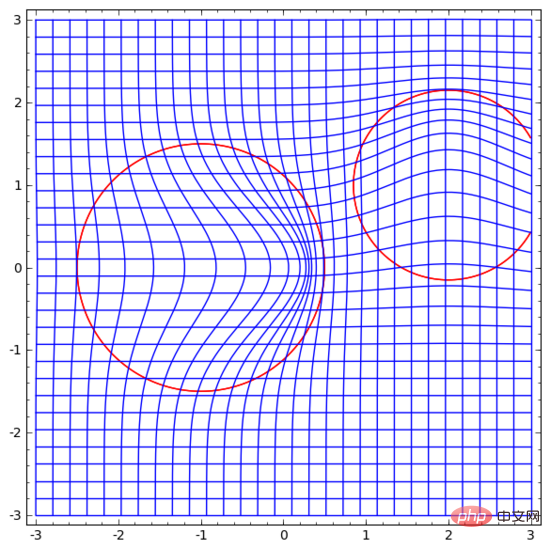
Nous pouvons apprendre des champs vectoriels à des points fixes (il suffit de choisir quelques points fixes dans l'ensemble d'entraînement comme ancres) et de les interpoler d'une manière ou d'une autre. Le champ vectoriel ci-dessus a la forme :

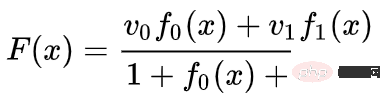
où et sont des vecteurs, et sont des fonctions gaussiennes à n dimensions. Cette idée s'inspire des fonctions de base radiale.

9. Couche K-Nearest Neighbour

Mon autre point est que la séparabilité linéaire peut être trop élevée et une exigence déraisonnable pour les réseaux de neurones. Il serait peut-être préférable d'utiliser le k-voisin le plus proche (k-NN). Cependant, l'algorithme k-NN repose fortement sur la représentation des données. Par conséquent, une bonne représentation des données est nécessaire pour que l'algorithme k-NN obtienne de bons résultats.

Dans la première expérience, j'ai entraîné certains réseaux de neurones MNIST (CNN à deux couches, sans décrochage) avec un taux d'erreur inférieur à 1 %. Ensuite, j'ai abandonné la dernière couche softmax et utilisé l'algorithme k-NN, et à plusieurs reprises, les résultats ont montré que le taux d'erreur était réduit de 0,1 à 0,2 %.

Cependant, j'estime que cette approche est toujours erronée. Le réseau neuronal essaie toujours de classer de manière linéaire, mais comme il utilise l'algorithme k-NN, il peut légèrement corriger certaines des erreurs qu'il commet, réduisant ainsi le taux d'erreur.

En raison de la pondération (1/distance), k-NN est différenciable selon la représentation des données sur laquelle il agit. Par conséquent, nous pouvons directement entraîner le réseau neuronal à la classification k-NN. Cela peut être considéré comme une couche « voisin le plus proche », qui agit de la même manière qu'une couche softmax.

Nous ne voulons pas renvoyer l'intégralité de l'ensemble de formation pour chaque mini-lot car cela coûte trop cher en termes de calcul. Je pense qu'une bonne approche serait de classer chaque élément du mini-lot en fonction de la catégorie des autres éléments du mini-lot, en donnant à chaque élément un poids de (1/(distance de la cible de classification)).

Malheureusement, même avec des architectures complexes, l'utilisation de l'algorithme k-NN ne peut réduire le taux d'erreur qu'à 4 à 5 %, alors qu'en utilisant des architectures simples, le taux d'erreur est plus élevé. Cependant, je n’ai pas mis beaucoup d’efforts sur les hyperparamètres.

Mais j'aime toujours l'algorithme k-NN car il est plus adapté aux réseaux de neurones. Nous voulons que les points d’une même variété soient plus proches les uns des autres, plutôt que d’insister sur l’utilisation d’hyperplans pour séparer les variétés. Cela revient à réduire une seule variété tout en agrandissant l’espace entre les variétés de différentes catégories. Cela simplifie le problème.

10. Résumé

Certaines caractéristiques topologiques des données peuvent empêcher ces données d'être séparées linéairement à l'aide de réseaux neuronaux de basse dimension (quelle que soit la profondeur du réseau neuronal). Même là où cela est techniquement réalisable, comme les spirales, la séparation est très difficile à réaliser avec des réseaux neuronaux de faible dimension.

Afin de classer avec précision les données, les réseaux de neurones nécessitent parfois des couches plus larges. De plus, les couches de réseaux neuronaux traditionnelles ne sont pas adaptées à la manipulation de variétés ; même si les poids sont définis manuellement, il est difficile d'obtenir une représentation idéale de transformation de données. De nouvelles couches de réseaux neuronaux pourraient jouer un rôle de soutien important, en particulier de nouvelles couches de réseaux neuronaux inspirées par la compréhension de l’apprentissage automatique sous un angle multiple.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!