Comment trouver des nombres premiers en javascript

Comment trouver les nombres premiers : 1. Parcourez tous les nombres naturels compris entre 1 et n et divisez par n. Si le reste est 0, cela signifie que le nombre n n'est pas un nombre premier, sinon c'est un nombre premier. La syntaxe est "for(i=2;i

L'environnement d'exploitation de ce tutoriel : système Windows 7, JavaScript version 1.8.5, ordinateur Dell G3.

Le concept des nombres premiers

Les nombres premiers sont également appelés nombres premiers. Un nombre premier fait référence à un nombre qui n'est pas divisible par d'autres nombres naturels sauf 1 et lui-même parmi les nombres naturels supérieurs à 1.

Nombres premiers inférieurs à 100 : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 25 au total.

Quatre façons de déterminer les nombres premiers en JavaScript

1. Les nombres premiers ne peuvent être divisibles que par 1 et par eux-mêmes

Les nombres premiers ne peuvent être divisibles que par 1 et par eux-mêmes, alors parcourez tous les nombres naturels dans le (1, n) intervalle ouvert pour diviser par n. S'il existe une division entière, c'est-à-dire que le reste est 0, cela signifie que le nombre n n'est pas un nombre premier, sinon c'est un nombre premier.

function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>Mais la complexité de cet algorithme est O(n)</p><h3 id="%E7%B4%A0%E6%95%B0%E5%B9%B3%E6%96%B9%E6%A0%B9%E8%8C%83%E5%9B%B4"><strong>2, et la plage des racines carrées des nombres premiers</strong></h3><p>En supposant que n n'est pas un nombre premier, alors n ne peut pas seulement être divisé par 1 et n, mais peut également être divisé par i et j. Autrement dit, n / i = j...0. Par exemple, 15 n'est pas un nombre premier, 15 / 3 = 5. Par exemple, 35 n'est pas un nombre premier. , 35 / 5 = 7. À ce stade, i et j doivent être dans (1, Math.sqrt(n) ] et [Math.sqrt(n), n), par exemple, Math.sqrt(15) ≈ 3,8 , alors 3 est dans (1, 3.8] et 5 est dans [3.8, 15). Par exemple, Math.sqrt(4) = 2, alors 2 est dans (1,2] et aussi dans [2,4). </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>À l'heure actuelle, la complexité de l'algorithme est O(sqrt(n))</p><h3 id="%E7%B4%A0%E6%95%B0%E4%B8%8D%E8%83%BD%E6%98%AF%E9%99%A4%E4%BA%862%E5%A4%96%E7%9A%84%E5%81%B6%E6%95%B0"><strong>3 Les nombres premiers ne peuvent pas être d'autres nombres pairs autres que 2</strong></h3><p>Sauf 2, tous les nombres pairs ne sont pas des nombres premiers</p><p><img src="https://img.php.cn/upload/image/644/149/762/1663645614907138.png" title="1663645614907138.png" alt="Comment trouver des nombres premiers en javascript">. </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  if (n % 2 === 0) {
    return false;
  }
 
  for (let i = 3; i <p>n dans la boucle for, Seule la partie bleu clair de l'image ci-dessus. </p><p>Donc l'algorithme ci-dessus réduit la boucle de moitié, et la complexité temporelle est O(sqrt(n) / 2) </p><p>Il convient de noter que le code de cet algorithme ne peut pas ajouter la condition de jugement de n % 2 === 0 à la boucle, le code suivant présente une vulnérabilité</p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 3; i <p>À ce stade, 4, 6 et 8 seront tous jugés comme des nombres premiers. </p><p>La raison de cette vulnérabilité est que la condition de boucle i </p><p>Cet algorithme ne peut garantir que la valeur n de n lorsque la condition de boucle i = i^2 = 9. </p><h3 id="%E5%A4%A7%E4%BA%8E%E7%AD%89%E4%BA%8E5%E7%9A%84%E7%B4%A0%E6%95%B0%E4%B8%80%E5%AE%9A%E5%92%8C6%E7%9A%84%E5%80%8D%E6%95%B0%E7%9B%B8%E9%82%BB"><strong>4. Les nombres premiers supérieurs ou égaux à 5 doivent être adjacents à des multiples de 6</strong></h3><p>Les nombres premiers supérieurs ou égaux à 5 doivent être adjacents à des multiples de 6</p><p>(Notez que cette phrase n'est pas équivalente à : <span style="text-decoration:line-through;"> est adjacent à des multiples de 6 Le nombre voisin doit être un nombre premier supérieur à 5</span>, cette conclusion n'est pas vraie)</p><p><img src="https://img.php.cn/upload/image/346/360/896/166364562667908Comment%20trouver%20des%20nombres%20premiers%20en%20javascript" title="166364562667908Comment trouver des nombres premiers en javascript" alt="Comment trouver des nombres premiers en javascript"></p><p>Comme le montre la figure ci-dessus, les nombres supérieurs ou égaux à 5 sont divisés en : 6y -1, 6a, 6a+1, 6a+2, 6a +3, 6a+4 (y>=1)</p><p>Parmi eux, 6a, 6a+2, 6a+3 et 6a+4 ne peuvent pas être des nombres premiers. . Seuls 6a-1 et 6a+1<strong><span   style="max-width:90%">peuvent</span></strong>être des nombres premiers . </p><p>De plus, 6a-1 (y>=1) et 6a + 5 (y>=0) sont équivalents. </p><p>Ainsi, nous pouvons exclure directement les nombres où n n'est pas 6y-1 (ou 6y+5) et 6y+1. La méthode d'élimination est </p><pre class="brush:js;toolbar:false">  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }

Ensuite, nous devons éliminer 6y-1 (ou 6y+5). ) et 6y Le nombre non premier en +1,

  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }

Il peut y avoir deux choses qui vous semblent confuses ici :

• Pourquoi l'incrément de i dans la boucle for est 6
• Pourquoi la condition pour déterminer nombres premiers dans la boucle for n % i = == 0 || n % (i+2) === 0

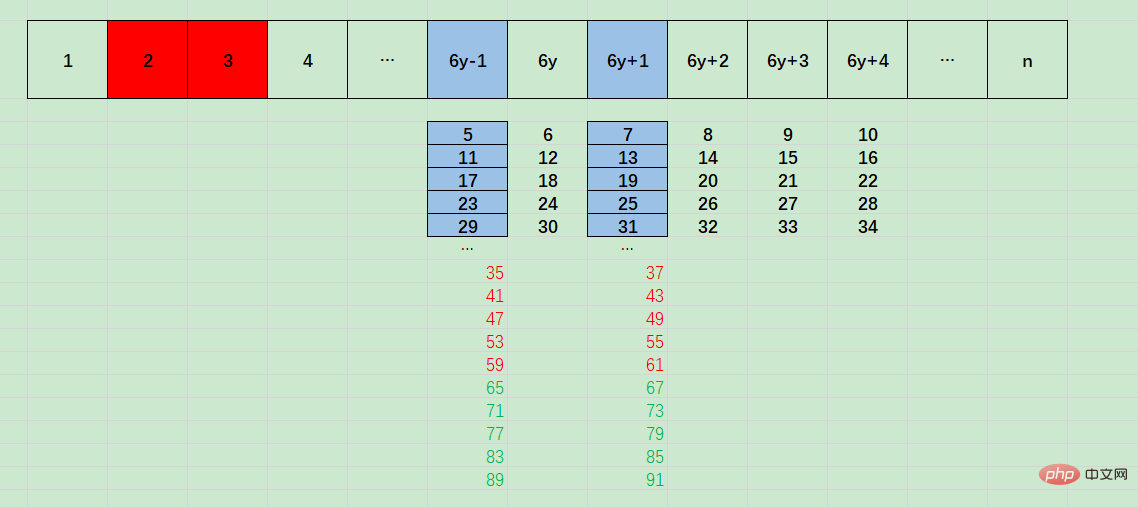
En regardant le diagramme ci-dessus, nous pouvons constater que 6y-1 est une arithmétique séquence avec une base de 5 et une différence de 6. Soit 5 + 6x :

• 对于 5 + 6x 而言，如果x为5的倍数（5 * z），则5 + 6x = 5 + 6 * 5 * z = 5 *（1+6z）,则此时5 + 6x可以被5整除。
• 5 + 6x 还可以转化为 5 + 6 + 6 * (x-1) = 11 + 6(x-1)，则只要x-1为11的倍数，则5 + 6x可以被11整除，
• 5 + 6x 还可以转化为 5 + 12 + 6 * (x-2) = 17 + 6(x-2)，则只要x-2为17的倍数，则5 + 6x可以被17整除
• ......

6y+1，是基数为7，差值为6的等差数列，即 7 + 6x :

• 对于 7 + 6x 而言，如果x为7的倍数（7 * z），则7 + 6x = 7 + 6 * 7 * z = 7 *（1+6z）,则此时7 + 6x可以被7整除。
• 7 + 6x 还可以转化为 7 + 6 + 6 * (x-1) = 13 + 6(x-1)，则只要x-1为13的倍数，则7 + 6x可以被13整除，
• 7 + 6x 还可以转化为 7 + 12 + 6 * (x-2) = 19 + 6(x-2)，则只要x-2为19的倍数，则7 + 6x可以被19整除，
• ......

所以6y-1和6y+1可能整除的数自增量为6，这是for循环i自增为啥是 6的原因

且6y-1和6y+1的整除数基数为5和7，相差为2，这是for循环中素数判定的条件为啥是 n % i === 0 || n % (i+2) === 0的原因

function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }
 
  for (let i = 5; i <p>此时时间复杂度为 O（sqrt(n) / 3） <br></p><p>【相关推荐：<a href="https://www.php.cn/course/list/17.html" target="_blank" textvalue="javascript视频教程">javascript视频教程</a>、<a href="https://www.php.cn/course/list/91.html" target="_blank" textvalue="编程基础视频">编程基础视频</a>】</p>

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!