Apprenez à implémenter le tri par fusion avec JavaScript

Colonne

javascript Dans cet article, nous apprenons la logique derrière le tri par fusion et l'implémentons en JavaScript. Enfin, le tri par fusion est comparé à d’autres algorithmes en termes de complexité spatiale et temporelle.

Recommandé (gratuit) : JavaScript (Vidéo)

La logique derrière le tri par fusion

Le tri par fusion trie une liste donnée d'éléments en utilisant le concept de diviser pour régner. Il divise un problème en sous-problèmes plus petits jusqu'à ce qu'ils deviennent suffisamment simples pour être résolus directement.

Voici les étapes du tri par fusion :

1. Divisez la liste donnée en deux (si la liste contient un nombre impair d'éléments, rendez-les à peu près égaux).
2. Continuez à diviser les sous-tableaux de la même manière jusqu'à ce qu'il ne reste qu'un seul tableau d'éléments.
3. À partir d'un seul tableau d'éléments, fusionne les sous-tableaux afin que chaque sous-tableau fusionné soit trié.
4. Répétez l'étape 3 jusqu'à ce que vous obteniez enfin un tableau trié.

En prenant le tableau [4, 8, 7, 2, 11, 1, 3] comme exemple, voyons comment fonctionne le tri par fusion :

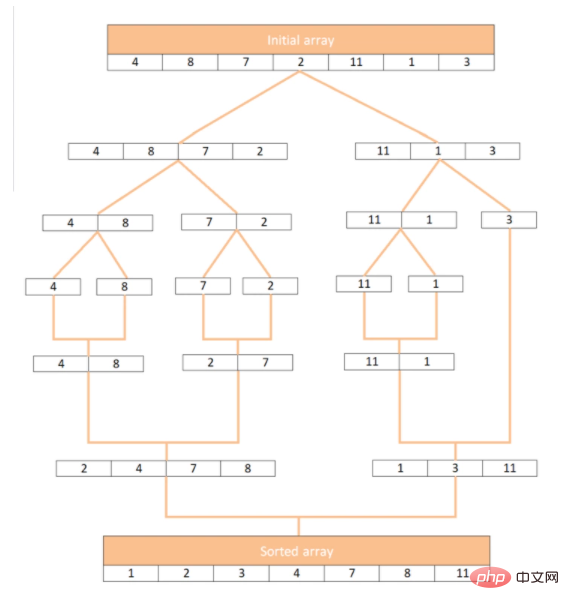
Utilisez JavaScript pour Implement merge Sorting

implémente d'abord une fonction merge() qui fusionne deux sous-tableaux triés en un seul tableau trié. Il est très important de noter que les deux sous-tableaux sont déjà triés et que la fonction merge() n'est utilisée que pour les fusionner.

peut être obtenu en parcourant ces deux sous-tableaux :

function merge(left, right) {
    let arr = []
    // 如果任何一个数组为空，就退出循环
    while (left.length && right.length) {
        // 从左右子数组的最小元素中选择较小的元素
        if (left[0] <p>Dans cette fonction, il est obtenu en fusionnant deux sous-tableaux triés (<code>left</code>, <code>right</code>) Un grand trié tableau. Tout d’abord, créez un tableau vide. Prenez ensuite le plus petit des plus petits éléments des deux sous-tableaux <code>left</code> et <code>right</code> et ajoutez-le au tableau vide. Il suffit de vérifier le premier élément des sous-tableaux <code>left</code> et <code>right</code> puisqu'ils sont triés. </p><p>Dans ce processus, l'élément sélectionné est supprimé du sous-tableau (implémenté par la fonction <code>shift()</code>). Continuez ce processus jusqu'à ce que l'un des sous-tableaux devienne vide. Enfin, insérez les éléments restants du sous-tableau non vide (car ils ont été triés) à la fin du tableau principal. </p><p>Maintenant que nous avons le code pour fusionner deux tableaux triés, voici le code final pour implémenter l'algorithme de tri par fusion. Cela signifie continuer à diviser le tableau jusqu'à ce que vous obteniez un tableau contenant un seul élément : </p><pre class="brush:php;toolbar:false">function mergeSort(array) {
  const half = array.length / 2
  
  if(array.length <p>Dans le code, déterminez d'abord le point médian et utilisez la fonction <code>splice()</code> pour diviser le tableau en deux sous-tableaux. Si le nombre d'éléments est impair, le nombre d'éléments à gauche sera un de moins. Continuez à diviser le tableau jusqu'à ce qu'il reste un tableau d'éléments uniques (<code>array.length ). Fusionnez ensuite les sous-tableaux à l'aide de la fonction <code>merge()</code> implémentée précédemment. </code></p><p>Une fois le code implémenté, testez-le avec le cas d'utilisation précédent : </p><pre class="brush:php;toolbar:false">array = [4, 8, 7, 2, 11, 1, 3];
console.log(mergeSort(array));

Le résultat est conforme aux attentes :

1,2,3,4,7,8,11

Efficacité du tri par fusion

La complexité temporelle dans le pire des cas du tri par fusion est $O(n\log n)$, ce qui est la même que la complexité temporelle dans le meilleur des cas du tri rapide. Le tri par fusion est l'un des algorithmes de tri les plus rapides actuellement disponibles.

Contrairement au tri rapide, le tri par fusion n'est pas un algorithme de tri sur place, ce qui signifie qu'il prend de l'espace supplémentaire en plus du tableau d'entrée. En effet, nous utilisons un tableau auxiliaire pour stocker les sous-tableaux. La complexité spatiale du tri par fusion est $O(n)$.

Un autre avantage du tri par fusion est qu'il est très adapté au multithreading, car chaque moitié divisée peut être triée indépendamment. Un autre moyen courant de réduire le temps d'exécution du tri par fusion consiste à utiliser le tri par insertion lorsque vous atteignez un sous-tableau relativement petit (environ 7 éléments). En effet, le tri par insertion fonctionne très bien avec des tableaux petits ou presque triés.

Résumé

Dans cet article, nous avons découvert la logique derrière l'algorithme Merge Sort et l'avons implémenté en JavaScript. C'est l'un des algorithmes de tri de base et peut nous aider à mieux comprendre la stratégie diviser pour régner.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!