À propos des propriétés des lignes de canevas

Cet article présente principalement des informations pertinentes sur l'explication détaillée des propriétés des lignes de toile. L'éditeur pense qu'il est assez bon, je vais donc le partager avec vous maintenant et le donner comme référence. Suivons l'éditeur pour y jeter un œil.

1. Line Cap lineCap

Valeur : bout (valeur par défaut), tête ronde, carré

var canvas=document.getElementById("canvas");

canvas.width=800;
canvas.height=800;

var context=canvas.getContext("2d");

context.lineWidth=40;
context.strokeStyle="#005588";

//三个beginpath()画了3条平行线
context.beginPath();
context.moveTo(100,200);
context.lineTo(700,200);
context.lineCap="butt";
context.stroke();

context.beginPath();
context.moveTo(100,400);
context.lineTo(700,400);
context.lineCap="round";
context.stroke();

context.beginPath();
context.moveTo(100,600);
context.lineTo(700,600);
context.lineCap="square";
context.stroke();

//baseline
context.lineWidth=1;
context.strokeStyle="#27a";
context.moveTo(100,100);
context.lineTo(100,700);
context.moveTo(700,100);
context.lineTo(700,700);
context.stroke();

rond Lors de l'animation, les coins arrondis peuvent être dessinés directement, et l'effet de lineCap est uniquement Can être utilisé au début et à la fin des segments de ligne, mais pas aux connexions.

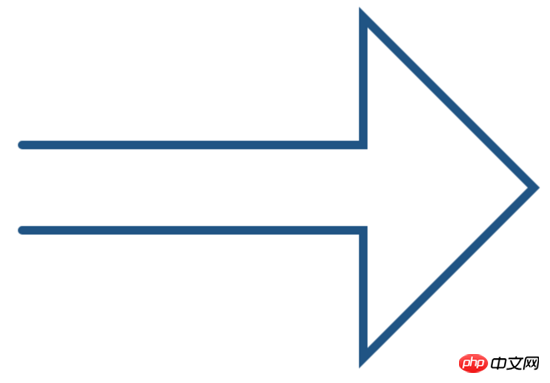
lineCap="square" peut être utilisé pour fermer complètement le segment de ligne lorsqu'il est fermé, mais il est toujours recommandé d'utiliser ClothPath() pour la fermeture.

var canvas=document.getElementById("canvas");

canvas.width=800;
canvas.height=800;

var context=canvas.getContext("2d");

context.beginPath();
context.moveTo(100, 350);
context.lineTo(500,350);
context.lineTo(500,200);
context.lineTo(700,400);
context.lineTo(500,600);
context.lineTo(500,450);
context.lineTo(100,450);
context.lineTo(100,350);
// context.closePath(); //推荐

context.lineWidth=10;
context.lineCap="square"; //不推荐
context.fillStyle="yellow";
context.strokeStyle="#058"

context.fill();
context.stroke();

2. Dessinez une étoile à cinq branches pour expliquer les autres attributs de statut de la ligne

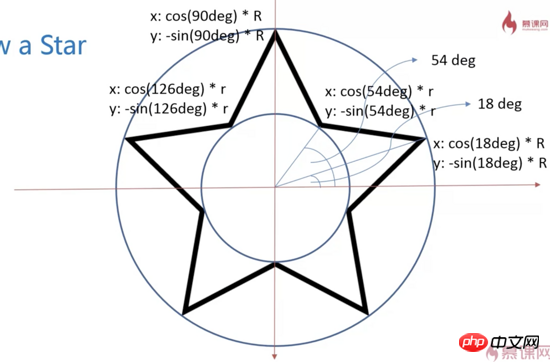
Les cinq angles du cercle se coupent en deux à 360°, chaque angle est de 72°, 90°-72°=18°

Les angles du petit cercle bissecter 72°, 18 °+36°=54°

Angle en radians - radians = angle*π/180 Soit (18+i*72)*Math.PI/180

var canvas=document.getElementById("canvas");

canvas.width=800;
canvas.height=800;

var context=canvas.getContext("2d");
context.beginPath();
//角度转弧度：除以180*PI
for(var i=0;i<5;i++){
    context.lineTo(Math.cos((18+i*72)/180*Math.PI)*300+400,
        -Math.sin((18+i*72)/180*Math.PI)*300+400);
    context.lineTo(Math.cos((54+i*72)/180*Math.PI)*150+400,
        -Math.sin((54+i*72)/180*Math.PI)*150+400);
}

context.closePath();

context.lineWidth=10;
context.stroke();

est encapsulé dans une fonction :

window.onload=function(){
    var canvas=document.getElementById("canvas");

    canvas.width=800;
    canvas.height=800;

    var context=canvas.getContext("2d");
    context.lineWidth=10;
    drawStar(context,150,300,400,400)
}        

function drawStar(ctx,r,R,x,y,){
    ctx.beginPath();
    //角度转弧度：除以180*PI
    for(var i=0;i<5;i++){
        ctx.lineTo(Math.cos((18+i*72)/180*Math.PI)*R+x,
            -Math.sin((18+i*72)/180*Math.PI)*R+y);
            ctx.lineTo(Math.cos((54+i*72)/180*Math.PI)*r+x,
            -Math.sin((54+i*72)/180*Math.PI)*r+y);
    }

    ctx.closePath();
    ctx.stroke();
}

Modifiez respectivement le petit r=80,200, 400 obtient le graphique suivant

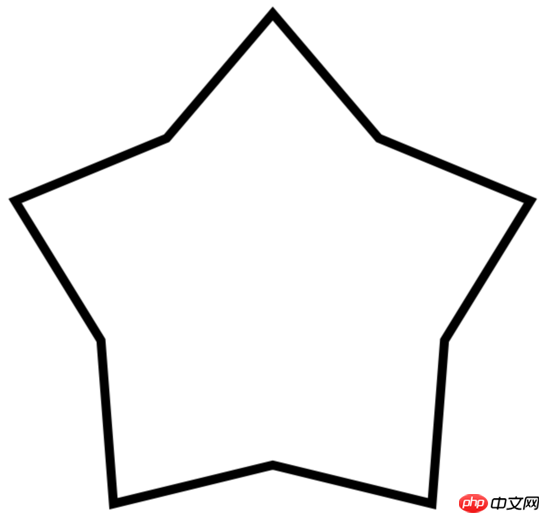
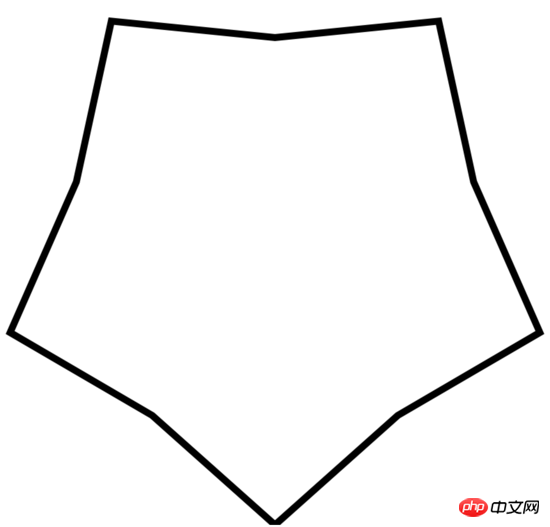
Ajouter un sens des aiguilles d'une montre paramètre de rotation : rot

window.onload=function(){
    var canvas=document.getElementById("canvas");

    canvas.width=800;
    canvas.height=800;

    var context=canvas.getContext("2d");
    context.lineWidth=10;
    drawStar(context,150,300,400,400,30);
}        




//rot顺时针旋转的角度
function drawStar(ctx,r,R,x,y,rot){
    ctx.beginPath();
    //角度转弧度：除以180*PI
    for(var i=0;i<5;i++){
        ctx.lineTo(Math.cos((18+i*72-rot)/180*Math.PI)*R+x,
            -Math.sin((18+i*72-rot)/180*Math.PI)*R+y);
            ctx.lineTo(Math.cos((54+i*72-rot)/180*Math.PI)*r+x,
            -Math.sin((54+i*72-rot)/180*Math.PI)*r+y);
    }

    ctx.closePath();
    ctx.stroke();
}

L'effet d'une rotation de 30 degrés est le suivant :

3. Lines Connect lineJoin et miterLimit

1 La valeur de lineJoin

miter(par défaut) présente toujours un coin pointu, un onglet en biseau, et coin arrondi

Le biseau est comme l'effet d'un ruban replié.

2. Attributs miterLimit liés à Mitre

Définissez le petit r à 30, lineJoin est en onglet, l'effet est le suivant : les coins ne sont pas prolongés en angles vifs, mais sont affichés sous forme de biseau.

context.lineJoin="miter";
drawStar(context,30,300,400,400,30);

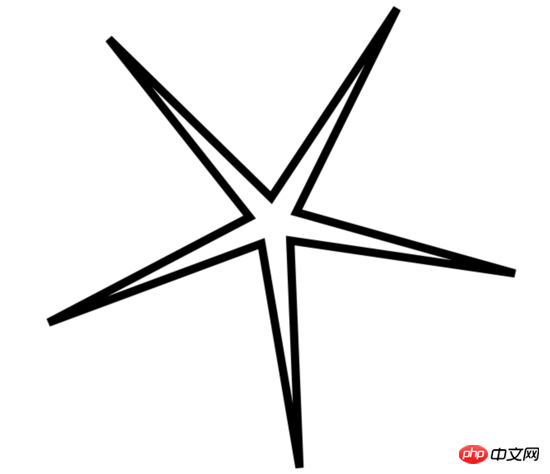
Pourquoi ?

Étant donné que la valeur par défaut de context.miterLimit=10 est 10,

miterlimit ne sera efficace que lorsque lineJoin est à onglet.

miterLimit fait référence à la valeur maximale de la distance résultante entre les angles intérieurs et extérieurs lors de l'utilisation de l'onglet comme moyen de connecter des lignes.

La valeur par défaut est 10, ce qui signifie que la valeur maximale est de 10px. Une fois qu'elle dépasse 10px, elle sera affichée en mode biseau.

Lorsque le rayon du cercle intérieur r est réglé sur 30 au-dessus, l'angle aigu formé est très aigu et la distance entre le coin intérieur et le coin extérieur dépasse la limite d'onglet de 10.

Maintenant augmentez la miterlimit à 20, l'effet est le suivant :

context.lineJoin="miter";
 context.miterLimit=20;
 drawStar(context,30,300,400,400,30);

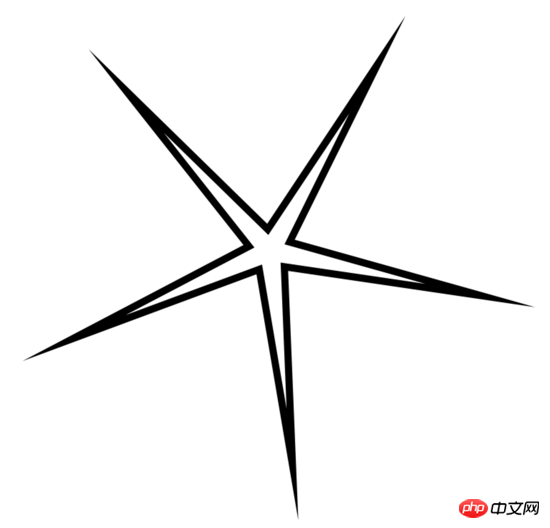
Remarque : miterLimit n'est pas la distance de de la pointe blanche à la pointe noire, cette distance est bien supérieure à 20px.

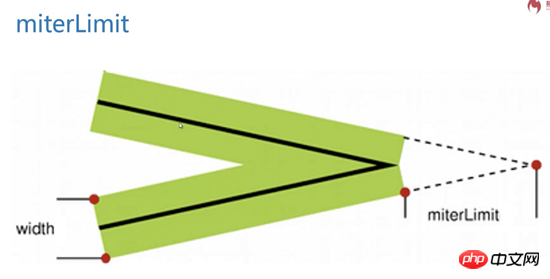
Lorsque miterLimit est généré, la ligne doit avoir une largeur et le coin pointu de la ligne médiane de la ligne avec largeur est la distance directe du coin pointu extérieur.

canvas donne une valeur d'expérience mitreLimit de 10. Ce n'est que dans des circonstances extrêmement particulières, lorsque des angles très aigus doivent être représentés, que miterLimit doit être modifié.

Ce qui précède représente l'intégralité du contenu de cet article. J'espère qu'il sera utile à l'étude de chacun. Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois !

Recommandations associées :

Comment utiliser HTML pour tracer une ligne verticale entre deux balises div

Comment utiliser HTML5 La toile réalise des flocons de neige qui tombent

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!