Comment dessiner un polygone basé sur des points aléatoires dans le canevas

Cet article présente principalement les informations pertinentes sur la façon de dessiner un polygone basé sur des points aléatoires dans le canevas. Le contenu est assez bon, je vais le partager avec vous maintenant et le donner comme référence.

Cause

Quand j'étudiais le livre "HTML5+Javascript Animation Basics" aujourd'hui, j'en ai parlé dans la troisième section du chapitre 8 Apprenez à utiliser trois ressorts pour relier trois points afin d'effectuer des exercices d'étirement.

Après avoir terminé l'exemple, j'ai réfléchi à ce qui se passerait si c'était quatre points ou cinq points.

J'ai réécrit le code pour rendre le nombre de points variable. L'effet final est de réaliser le mouvement d'étirement final de chaque point pour équilibrer, mais les connexions entre les points ne sont pas très belles, et certaines sont croisées.

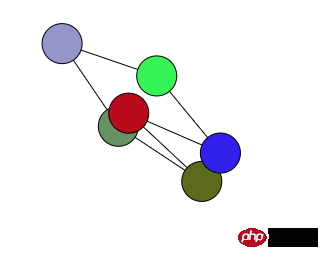
J'ai donc réfléchi à la possibilité d'optimiser cette zone.

Faites pivoter la connexion

Les points de l'exemple précédent sont tous dans des positions aléatoires, la connexion est donc incontrôlable. Je veux donc commencer par cela en premier.

Utilisez d'abord un certain point comme point de référence pour obtenir les angles d'autres points par rapport à ce point.

Connectez ensuite ces points selon l'angle du petit au grand, afin de pouvoir dessiner un polygone normal.

Le code approximatif d'implémentation est le suivant :

let balls = [];
let ballNum = 6;
let firstBall = null;
while(ballNum--) {
  let ball = new Ball(20, parseColor(Math.random() * 0xffffff))
  ball.x = Math.random() * width;
  ball.y = Math.random() * height;
  balls.push(ball)

  if (!firstBall) {
    firstBall = ball
    ball.angle = 0
  } else {
    const dx = ball.x - firstBall.x,
          dy = ball.y - firstBall.y;

    ball.angle = Math.atan2(dy, dx);
  }
}

// 尝试让球连线是一个正多边形
balls = balls.sort((ballA, ballB) => {
  return ballA.angle - ballB.angle
})

De cette façon, lorsque la connexion est tracée à la fin, le tableau peut être parcouru du petit au grand angle Venez dessiner.

L'effet est le suivant :

Cela peut réduire considérablement le nombre de lignes qui se croisent, mais cela ne peut toujours pas être complètement évité.

Ensuite, je veux essayer d'optimiser cette solution, par exemple en utilisant Math.abs pour corriger l'angle, ou en trouvant le point avec le plus petit angle pour relier chaque point. Mais le résultat n’est pas bon, il est impossible d’éviter de franchir les lignes.

Rotation basée sur le point central

J'ai pensé à une autre idée plus tard. Si le point central du polygone peut être déterminé, alors calculez. les positions relatives de tous les points par rapport au centre séparément. L'angle entre les points peut être utilisé pour relier ces points dans le sens des aiguilles d'une montre ou dans le sens inverse.

Mais après de longues recherches sur Internet, tous les algorithmes de points nécessitent une série de points disposés dans un certain ordre dans le sens des aiguilles d'une montre.

Mais si j'ai ces points, je peux déjà dessiner un polygone. J'ai dû abandonner

Segmentation bipolaire sur l'axe X

En désespoir de cause, j'ai dû faire une recherche sur Google, puis j'ai trouvé un réponse sur Zhihu qui était plutôt bonne : Comment connecter un ensemble non ordonné de points sur le plan en un simple polygone ?

Pour la description spécifique de l'algorithme, regardez simplement la réponse et je n'entrerai pas dans les détails.

Cependant, lors de la connexion de la chaîne supérieure et de la chaîne inférieure, il vous suffit de vous assurer que la chaîne supérieure est connectée par ordre décroissant sur l'axe X et que la chaîne inférieure est connectée par ordre croissant sur l'axe X ( dessiné dans le sens inverse des aiguilles d’une montre). Quant aux points ayant le même axe X, peu importe que l’axe Y soit plus grand ou plus petit.

Une fois implémenté, il est implémenté strictement selon l'algorithme de la réponse.

Pour juger si un point appartient à la chaîne supérieure ou à la chaîne inférieure, l'idée initiale est de déterminer l'équation fonctionnelle de la ligne droite basée sur deux points, puis d'introduire les coordonnées des points pour le calcul. Mais plus tard, j'ai pensé que tous les points utilisaient le pôle le plus à gauche pour calculer l'angle oblique, puis le divisons en fonction de la taille de l'angle, ce qui est plus facile à comprendre visuellement.

Le code approximatif est le suivant :

let balls = [];
let tempBalls = [];
let ballNum = 6;
let isDragingBall = false;

while(ballNum--) {
  let ball = new Ball(10, parseColor(Math.random() * 0xffffff))
  ball.x = Math.random() * width;
  ball.y = Math.random() * height;
  tempBalls.push(ball)
}

// 让点按X轴升序排序
tempBalls = tempBalls.sort((ballA, ballB) => {
  return ballA.x - ballB.x
})

// 找X轴左右极点
let firstBall = tempBalls[0],
    lastBall = tempBalls[tempBalls.length -1];
let smallXBalls = tempBalls.filter(ball => ball.x === firstBall.x),
    bigXBalls = tempBalls.filter(ball => ball.x === lastBall.x)

// 处理左右极点有多个的情况
if (smallXBalls.length > 1) {
  smallXBalls.sort((ballA, ballB) => {
    return ballB.y - ballA.y
  })
}
if (bigXBalls.length > 1) {
  bigXBalls.sort((ballA, ballB) => {
    return ballB.y - ballA.y
  })
}

firstBall = smallXBalls[0]
lastBall = bigXBalls[0]

// 获得极点连线的角度
let splitLineAngle = Math.atan2(lastBall.y - firstBall.y, lastBall.x - firstBall.x);
let upperBalls = [],
    lowerBalls = [];

// 所有其他点跟firstBall计算角度
// 大于splitLineAngle的都是下链
// 其他是上链
tempBalls.forEach(ball => {
  if (ball === firstBall || ball === lastBall) {
    return false
  }
  let angle = Math.atan2(ball.y - firstBall.y, ball.x - firstBall.x);
  if (angle > splitLineAngle) {
    lowerBalls.push(ball)
  } else {
    upperBalls.push(ball)
  }
})

// 处理X轴相同情况的排序
lowerBalls = lowerBalls.sort((ballA, ballB) => {
  if (ballA.x !== ballB.x) {
    return ballA.x - ballB.x
  }
  return ballB.y - ballA.y
})

upperBalls = upperBalls.sort((ballA, ballB) => {
  if (ballA.x !== ballB.x) {
    return ballB.x - ballA.x
  }
  return ballB.y - ballB.x
})

// 逆时针连接所有的点
balls = [firstBall].concat(lowerBalls, [lastBall], upperBalls)

balls = balls.map((ball, i) => {
  ball.text = i + 1;
  return ball
})

Les boules finalement rendues sont les points du polygone triés dans le sens inverse des aiguilles d'une montre.

L'effet est le suivant :

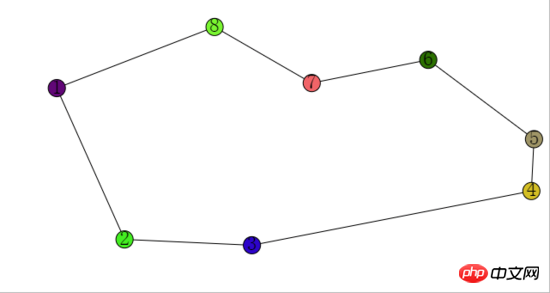
L'état interne de chaque balle est le suivant :

Ce qui précède est le résumé de cet article. Tout le contenu, j'espère qu'il sera utile à l'étude de chacun. Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois !

Recommandations associées :

Utilisez html5 Canvas encapsule un diagramme circulaire que les echarts ne peuvent pas implémenter

HTML5 Canvas implémente la méthode de dessin des courbes

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!