Maison >interface Web >tutoriel CSS >css3+js réalise un mouvement planétaire en 3D
css3+js réalise un mouvement planétaire en 3D
- php中世界最好的语言original
- 2018-03-22 13:41:082200parcourir
Cette fois, je vais vous apporter css3+js pour réaliser une opération planétaire 3D. Quelles sont les précautions pour réaliser une opération planétaire 3D avec css3+js. Ce qui suit est un cas pratique, jetons un coup d'oeil.
Partie HTML
<p class="path-Saturn"> <p id="Saturn" title="土星"> <p class="x"></p> <p class="y"></p> <p class="z"></p> <p class="space space-x"></p> <p class="space space-x1"></p> <p class="space space-x2"></p> <p class="space space-y"></p> <p class="space space-y1"></p> <p class="space space-y2"></p> <p class="space space-z"></p> <p class="space space-z1"></p> <p class="space space-z2"></p> <!-- 卫星 --> <p class="path-satellite"> <p id="satellite" title="卫星"> <p class="x"></p> <p class="y"></p> <p class="z"></p> <p class="space space-x"></p> <p class="space space-x1"></p> <p class="space space-x2"></p> <p class="space space-y"></p> <p class="space space-y1"></p> <p class="space space-y2"></p> <p class="space space-z"></p> <p class="space space-z1"></p> <p class="space space-z2"></p> </p> </p> </p> </p>
Ici nous utilisons les trois premières catégories de p pour dessiner chaque planète : x, y, z x, Les axes y, z, et ces planètes peuvent être imbriquées, c'est-à-dire que, tout comme le code ci-dessus, les planètes intérieures sont les satellites des planètes extérieures.
partie CSS
.path-Saturn, .path-earth, .path-Venus, .path-Neptune, .path-Jupiter, .path-Mercury, .path-satellite, .path-moon{
position: absolute;
width: 95%;
height: 95%;
top: 2.5%;
left: 2.5%;
border: 1px solid #ddd;
border-radius: 50%;
transform: rotateX(60deg);
transform-style: preserve-3d;
}
#sun, #earth, #Saturn, #Venus, #Neptune, #Jupiter, #Mercury, #satellite, #moon{
width: 160px;
height: 160px;
position: absolute;
transform-style: preserve-3d;
top: 50%;
left: 50%;
margin: -80px 0 0 -80px;
animation: rotateForward 10s linear infinite;
cursor: pointer;
transform: translateZ(-80px);
}
/*x, y, z轴*/
.x, .y, .z{
position: absolute;
height: 100%;
border: 1px solid #999;
left: 50%;
margin-left: -1px;
}
.y{
transform: rotateZ(90deg);
}
.z{
transform: rotateX(90deg);
}
@keyframes rotateForward {
0%{
transform: rotate3d(1, 1, 1, 0deg);
}
100%{
transform: rotate3d(1, 1, 1, -360deg);
}
}
/*Saturn*/
#Saturn{
width: 80px;
height: 80px;
left: 0%;
margin: -40px 0 0 -40px;
animation: rotateForward 4s linear infinite;
transform: translateZ(-40px);
}
#Saturn .space{
width: 80px;
height: 80px;
box-shadow: 0 0 60px rgba(90, 80, 53, 1);
background-color: rgba(90, 80, 53, .3);
}
#Saturn .space-x1, #Saturn .space-x2, #Saturn .space-y1, #Saturn .space-y2, #Saturn .space-z1, #Saturn .space-z2{
width: 87.5%;
height: 87.5%;
top: 6.25%;
left: 6.25%;
transform: rotate3d(0, 0, 0, 0deg) translateZ(20px);
}
#Saturn .space-x1{
transform: rotate3d(0, 0, 0, 0deg) translateZ(-20px);
}
#Saturn .space-y{
transform: rotate3d(0, 1, 0, 90deg) translateZ(0px);
}
#Saturn .space-y1{
transform: rotate3d(0, 1, 0, 90deg) translateZ(-20px);
}
#Saturn .space-y2{
transform: rotate3d(0, 1, 0, 90deg) translateZ(20px);
}
#Saturn .space-z{
transform: rotate3d(1, 0, 0, 90deg) translateZ(0px);
}
#Saturn .space-z1{
transform: rotate3d(1, 0, 0, 90deg) translateZ(-20px);
}
#Saturn .space-z2{
transform: rotate3d(1, 0, 0, 90deg) translateZ(20px);
}
Utilise principalement neuf faces pour reconstituer une sphère à travers diverses rotations et traductions. Et comme aucun code de compatibilité n'est écrit ici, les amis souhaitant télécharger le code source devraient essayer de l'ouvrir avec le navigateur Chrome. Plusieurs propriétés CSS3 doivent être mentionnées ici :
1. transform-style:preserve-3d; est utilisé pour afficher les éléments enfants du conteneur avec cette propriété définie dans un effet 3D.
2. transform-origin : définissez la position du point de base de la rotation et de la translation de l'élément pivoté.
3. perspective : définissez la vue dans laquelle l'élément est affiché.
Partie JS
(function(planetObj, TimeArr, judgeDirec) {
//检测参数是否规范
var timeRegexp = /^[1-9][0-9]*$/,
direcRegexp = /^[01]$/;
function checkArgs (arg, ele, regexp) {
if(arg){
$(arg).each(function (i, item) {
if(arg.length != planetObj.length || !regexp.test(item)){
throw Error('an error occured');
return;
}else{
return arg;
}
})
}else{
arg = [];
for(var i = 0; i < planetObj.length; i++){
arg.push(ele);
}
}
return arg;
}
TimeArr = checkArgs(TimeArr, 50, timeRegexp);
judgeDirec = checkArgs(judgeDirec, 1, direcRegexp);
var PathArr = [];
$(planetObj).each(function (i, item) {
var n = 0; //定义一个标识,来判断当前是怎么运动的
PathArr.push({
a : $(item).parent().width() / 2,
b : $(item).parent().height() / 2
});
//变化x坐标,然后根据椭圆轨迹,获得y坐标,以达到运动的效果
function getEllopsePath (x, PathObj) {
x = x - PathObj.a;
var m;
n ? (judgeDirec[i] ? m = 1 : m = -1) : (judgeDirec[i] ? m = -1 : m = 1); //判断开根号求得的y值是否为负数,从而确定旋转方向
// if(judgeDirec[i]){
// n ? (m = judgeDirec[i]) : (m = judgeDirec[i]-2);
// }else{
// n ? (m = judgeDirec[i] - 1) : (m = judgeDirec[i] + 1);
// }
return Math.sqrt((1 - x * x / (PathObj.a * PathObj.a)) * PathObj.b * PathObj.b) * m + PathObj.b;
}
function moving () {
var x = parseInt($(item).css('left'), 10);
if(x == 2 * PathArr[i].a){ //到达轨迹的右零界点的时候x减小
n--;
}else if (x == 0) { //到达轨迹的左临界点的时候,x增加
n++;
}
n ? x++ : x--;
$(item).css({
'top' : getEllopsePath(x, PathArr[i]) + 'px',
'left' : x + 'px'
});
}
setInterval(moving, TimeArr[i]);
});
})(['#Saturn', '#earth', '#Venus', '#Neptune', '#Mercury', '#Jupiter', '#satellite', '#moon'], [40, 180, 240, 20, 120, 200, 30, 10]/*option默认为50毫秒*/, [1, 0, 0, 0, 1, 0, 1, 1]/*option 判断运动方向,0为顺时针,1为逆时针,默认为逆时针*/);
Lors de la mise en œuvre du mouvement planétaire, il y a certains endroits qui ne sont pas très bien gérés, car je suis régulièrement intervalles, laissez la position gauche de la planète changer, puis trouvez la valeur de top selon la formule de l'ellipse. Parce que l’ellipse est inégale, le mouvement de la planète semblera rapide et lent, car sa valeur maximale change de manière inégale.
Ensuite, il y a une autre chose qui mérite attention ici, c'est-à-dire que les valeursextraites par la méthode Math.sqrt() sont toutes des nombres positifs, et si nous voulons que la planète tourne autour, nous besoin d'ajuster dynamiquement les extrémités gauche et droite de la trajectoire. Modifiez les nombres positifs et négatifs de la valeur générée par la méthode Math.sqrt().
Un rendu est joint ci-dessous
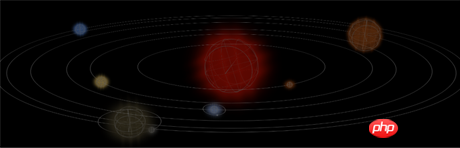
Je crois que vous maîtrisez la méthode après avoir lu le cas dans cet article , pour un contenu plus passionnant, veuillez prêter attention aux autres articles connexes sur le site Web php chinois !
Lecture recommandée :
Explication détaillée du chargement dynamique de CSS
Comment utiliser la propriété webkit-tap-highlight-color de CSS3
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

