MLP was killed overnight! MIT Caltech and other revolutionary KANs break records and discover mathematical theorems that crush DeepMind

Overnight, the machine learning paradigm is about to change!

Today, the infrastructure that dominates the field of deep learning is the multilayer perceptron (MLP)—which places activation functions on neurons.

So, besides this, are there any new routes we can take?

Just today, teams from MIT, California Institute of Technology, Northeastern University and other institutions released a major , a new neural network structure-Kolmogorov–Arnold Networks (KAN).

The researchers made a simple change to the MLP, that is, the learnable activation function is derived from the nodes (neurons) Move to the edge (weight)!

Paper address: https://arxiv.org/pdf/2404.19756

This changes at first glance It may seem baseless at first, but it has a profound connection with "approximation theories" in mathematics.

It turns out that the Kolmogorov-Arnold representation corresponds to a two-layer network, and there is a learnable activation function on the edges, not on the nodes.

Inspired by the representation theorem, researchers used neural networks to explicitly parameterize the Kolmogorov-Arnold representation.

It is worth mentioning that the origin of the name KAN is to commemorate the two great late mathematicians Andrey Kolmogorov and Vladimir Arnold.

Experimental results show that KAN has superior performance than traditional MLP, improving the accuracy and interpretability of neural networks.

The most unexpected thing is that the visualization and interactivity of KAN give it potential application value in scientific research and can help Scientists discover new mathematical and physical laws.

In the research, the author used KAN to rediscover the mathematical laws in knot theory!

Moreover, KAN replicated the results of DeepMind in 2021 with a smaller network and automation.

In terms of physics, KAN can help physicists study Anderson localization (which is a term in condensed matter physics a phase change).

By the way, all examples of KAN in the study (except parameter scanning) can be reproduced in less than 10 minutes on a single CPU.

The emergence of KAN directly challenged the MLP architecture that had always dominated the field of machine learning and caused an uproar across the entire network.

A new era of machine learning has begun

Some people say that a new era of machine learning has begun!

Google DeepMind research scientists said, "Kolmogorov-Arnold strikes again! A little-known fact is: this theorem appeared in a seminal paper on permutation invariant neural networks (depth sets), showing This illustrates the complex connection between this representation and the way ensembles/GNN aggregators are constructed (as a special case)."

A new neural network architecture was born! KAN will dramatically change the way artificial intelligence is trained and fine-tuned.

Is AI entering the 2.0 era?

Some netizens used popular language to make a vivid metaphor of the difference between KAN and MLP:

Kolmogorov-Arnold Network (KAN) is like a three-layer cake recipe that can bake any cake, while Multi-Layer Perceptron (MLP) is a customized cake with different number of layers. MLP is more complex but more general, while KAN is static but simpler and faster for one task.

The author of the paper, MIT professor Max Tegmark, said that the latest paper shows that a completely different architecture from the standard neural network can be used to process Achieve higher accuracy with fewer parameters when solving interesting physics and mathematics problems.

Next, let’s take a look at how KAN, which represents the future of deep learning, is implemented?

KAN back on the poker table

Theoretical basis of KAN

Kolmogorov-Arnold theorem (Kolmogorov–Arnold representation theorem) pointed out that if f is a multi-variable continuous function defined on a bounded domain, then the function can be expressed as a finite combination of multiple single-variable, additive continuous functions.

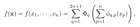
For machine learning, the problem can be described as: the process of learning a high-dimensional function can be simplified into learning a one-dimensional function of a polynomial quantity.

But these one-dimensional functions may be non-smooth, or even fractal, and may not be learned in practice. It is precisely because of this "pathological behavior" that Cole Mogorov-Arnold said that the theorem is basically a "death sentence" in the field of machine learning, that is, the theory is correct, but it is useless in practice.

In this article, the researchers are still optimistic about the application of this theorem in the field of machine learning and propose two improvements:

1. In the original equation, there are only two layers of nonlinearity and one hidden layer (2n 1), which can generalize the network to any width and depth;

2. Scientific and Most functions in daily life are mostly smooth and have sparse combinatorial structures that may contribute to smooth Kolmogorov-Arnold representations. Similar to the difference between physicists and mathematicians, physicists are more concerned with typical scenarios, while mathematicians are more concerned with worst-case scenarios.

KAN Architecture

The core idea of ​​Kolmogorov-Arnold Network (KAN) design is to transform the approximation problem of multi-variable functions into learning a set of single Variable function problem. Within this framework, every univariate function can be parameterized with a B-spline, which is a local, piecewise polynomial curve whose coefficients are learnable.

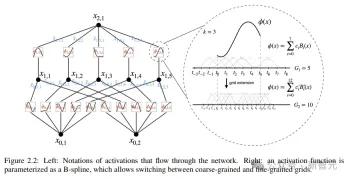
#In order to extend the two-layer network in the original theorem deeper and wider, the researchers proposed a more "generalized" version of the theorem To support the design of KAN:

Inspired by the cascading structure of MLPs to improve network depth, the article also introduces a similar concept, the KAN layer, which is composed of a one-dimensional function matrix, each Functions all have trainable parameters.

According to the Kolmogorov-Arnold theorem, the original KAN layer consists of internal functions and external functions, which correspond to different inputs. and output dimensions. This design method of stacking KAN layers not only expands the depth of KANs, but also maintains the interpretability and expressiveness of the network. Each layer is composed of univariate functions, and the functions can be learned independently. and understanding.

f in the following formula is equivalent to KAN

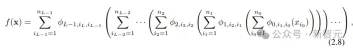
Implementation details

Although the design concept of KAN seems simple and relies purely on stacking, it is not easy to optimize. The researchers also explored some techniques during the training process.

1. Residual activation function: By introducing a combination of basis function b(x) and spline function, using the concept of residual connection to construct the activation function ϕ(x), we have Contribute to the stability of the training process.

#2. Initialization scales (scales): The initialization of the activation function is set to a spline function close to zero, and the weight w uses the Xavier initialization method, with Helps maintain gradient stability in the early stages of training.

3. Update the spline grid: Since the spline function is defined in a bounded interval, and the activation value may exceed this interval during the neural network training process, the spline is dynamically updated. The grid ensures that the spline function always operates within the appropriate interval.

Parameters

1. Network depth: L

2. Width of each layer :N

3. Each spline function is defined based on G intervals (G 1 grid point), k order (usually k=3)

So the number of parameters of KANs is about

#For comparison, the number of parameters of MLP is O(L*N^2), which seems to be better than KAN More efficient, but KANs can use smaller layer widths (N), which not only improves generalization performance but also improves interpretability.

What is KAN better than MLP?

Stronger performance

As a plausibility check, the researchers constructed five known smooth KAs (Kolmogorov-Arnold) The represented example is used as a validation data set. KANs are trained by adding grid points every 200 steps, covering the range of G as {3,5,10,20,50,100,200,500,1000}

Use MLPs of different depths and widths as baseline models, and both KANs and MLPs use the LBFGS algorithm for a total of 1800 training steps, and then use RMSE as an indicator for comparison.

It can be seen from the results that the curve of KAN is more jittery, can converge quickly, and reaches a stable state; and it is better than the scaling curve of MLP, especially in high-dimensional situations.

It can also be seen that the performance of three-layer KAN is much stronger than that of two-layer KAN, indicating that deeper KANs have stronger expressive capabilities, in line with expectations.

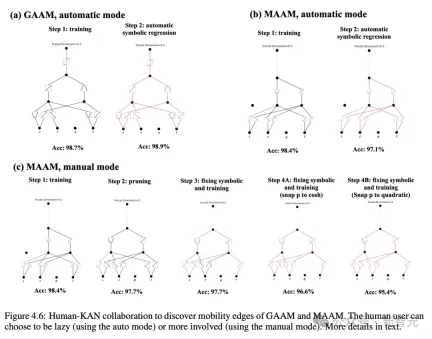
Interactive interpretation of KAN

The researchers designed a simple regression experiment to show that users can obtain The most interpretable results.

Assuming that the user is interested in finding out the symbolic formula, a total of 5 interactive steps are required.

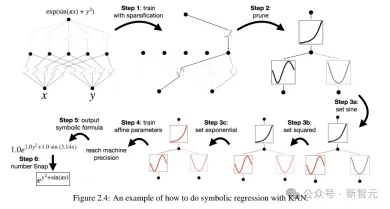
#Step 1: Training with sparsification.

Starting from a fully connected KAN, the network can be made sparser through training with sparse regularization, so that 4 out of 5 neurons in the hidden layer can be found None of them seem to have any effect.

Step 2: Pruning

After automatic pruning, discard all useless hidden neurons, leaving only one KAN. The activation function is matched to a known symbolic function.

Step 3: Set up the symbolic function

Assuming the user can correctly guess these symbolic formulas from staring at the KAN chart, they can set it directly

If the user has no domain knowledge or does not know which symbolic functions these activation functions may be, the researchers provide a function suggest_symbolic to suggest symbolic candidates .

Step 4: Further training

After all activation functions in the network are symbolized, the only remaining parameters are the affine parameters ;Continue training the affine parameters, and when you see the loss drop to machine precision, you will realize that the model has found the correct symbolic expression.

Step 5: Output symbolic formula

Use Sympy to calculate the symbolic formula of the output node and verify the correct answer.

Interpretability Verification

The researchers first designed six samples in a supervised toy data set to demonstrate the performance of the KAN network Combinatorial structural capabilities under symbolic formulas.

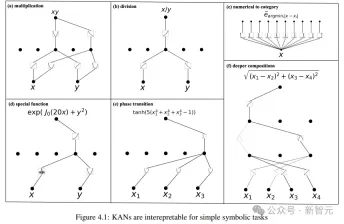
It can be seen that KAN has successfully learned the correct single variable function, and through visualization, it can explain KAN’s thinking process .

In an unsupervised setting, the data set only contains input features x. By designing the relationship between certain variables (x1, x2, x3), the KAN model can be tested to find The ability of dependencies between variables.

Judging from the results, the KAN model successfully found the functional dependency between variables, but the author also pointed out that it is still only synthesizing data. To conduct experiments on, a more systematic and controllable method is needed to discover the complete relationship.

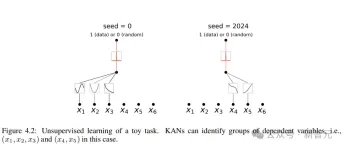
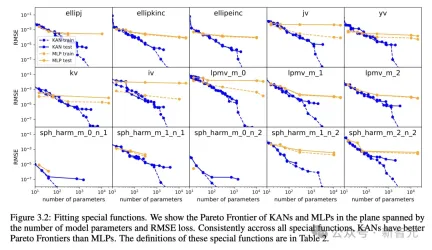
Pareto optimal

By fitting special functions, the author shows KAN and MLP The Pareto Frontier in the plane spanned by the number of model parameters and the RMSE loss.

Among all special functions, KAN always has a better Pareto front than MLP.

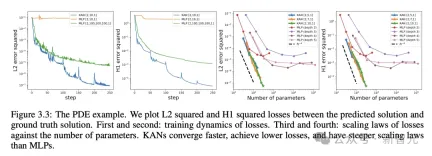
Solving Partial Differential Equations

In the task of solving partial differential equations, the researchers plotted the difference between the predicted and true solutions The L2 squared and H1 squared losses.

In the figure below, the first two are the training dynamics of the loss, and the third and fourth are the Sacling Law of the number of loss functions.

As shown in the results below, KAN converges faster, has lower loss, and has a steeper expansion law compared to MLP.

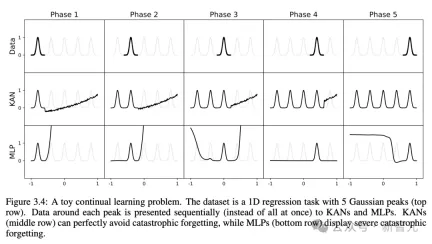
Continuous learning, catastrophic forgetting will not occur

We all know that catastrophic forgetting is A serious problem in machine learning.

The difference between artificial neural networks and the brain is that the brain has different modules that function locally in space. When learning a new task, structural reorganization occurs only in local areas responsible for the relevant skill, while other areas remain unchanged.

However, most artificial neural networks, including MLP, do not have this concept of locality, which may be the reason for catastrophic forgetting.

Research has proven that KAN has local plasticity and can use splines locality to avoid catastrophic forgetting.

The idea is very simple, since the spline is local, the sample will only affect some nearby spline coefficients, while the distant coefficients remain unchanged.

In contrast, since MLP usually uses global activation (such as ReLU/Tanh/SiLU), any local changes may propagate to distant regions uncontrollably, thereby destroying the information stored there.

The researchers used a one-dimensional regression task (composed of 5 Gaussian peaks). The data around each peak is presented to KAN and MLP sequentially (rather than all at once).

The results are shown in the figure below. KAN only reconstructs the area where data exists in the current stage, leaving the previous area unchanged.

And MLP will reshape the entire area after seeing new data samples, leading to catastrophic forgetting.

#Discover the knot theory, and the results surpass DeepMind

What does the birth of KAN mean for the future application of machine learning?

Knot theory is a discipline in low-dimensional topology. It reveals the topological problems of three-manifolds and four-manifolds, and is used in biology and topology. Quantum computing and other fields have a wide range of applications.

#In 2021, the DeepMind team used AI to prove the knot theory for the first time in Nature.

Paper address: https://www.nature.com/articles/s41586-021-04086-x

In this study, a new theorem related to algebraic and geometric knot invariants was derived through supervised learning and human domain experts.

That is, gradient saliency identifies key invariants of the supervision problem, which led domain experts to propose a conjecture that was subsequently refined and proven.

In this regard, the author studies whether KAN can achieve good interpretable results on the same problem to predict the signature of knots.

In the DeepMind experiment, the main results of their study of the knot theory data set are:

1 Using the network attribution method, it is found that the signature mainly depends on the intermediate distance and the vertical distance λ.

2 Human domain experts later discovered that had a high correlation with slope and concluded that

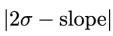
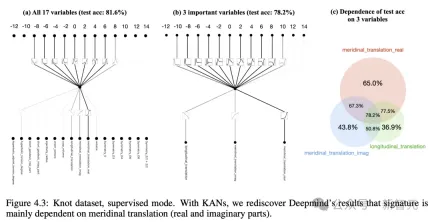
In order to study question (1), the author treats 17 knot invariants as input and signatures as output.

Similar to the setup in DeepMind, signatures (even numbers) are encoded as one-hot vectors, and the network is trained with a cross-entropy loss.

The results found that a very small KAN can achieve a test accuracy of 81.6%, while DeepMind’s 4-layer width 300MLP only achieved a test accuracy of 78%.

As shown in the table below, KAN (G = 3, k = 3) has about 200 parameters, while MLP has about 300,000 parameters.

It’s worth noting that KAN is not only more accurate; At the same time, the parameters are more efficient than MLP.

In terms of interpretability, the researchers scale the transparency of each activation according to its size, so it is immediately clear which input variables are important without feature attribution.

Then, KAN is trained on the three important variables and obtains a test accuracy of 78.2%.

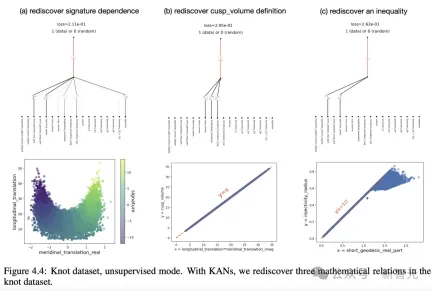
As follows, through KAN, the author rediscovered three mathematical relationships in the knot data set.

Physical Anderson localization is solved

And in physics applications, KAN has also played great value.

Anderson is a fundamental phenomenon in which disorder in a quantum system causes localization of the electron's wave function, bringing all transmission to a halt.

In one and two dimensions, the scaling argument shows that for any tiny random disorder, all electronic eigenstates are exponentially localized.

In contrast, in three dimensions, a critical energy forms a phase boundary that separates extended and localized states, which is called a mobility edge.

Understanding these mobility edges is critical to explaining a variety of fundamental phenomena such as metal-insulator transitions in solids, as well as the localization effects of light in photonic devices.

The author found through research that KANs make it very easy to extract mobility edges, whether numerically or symbolically.

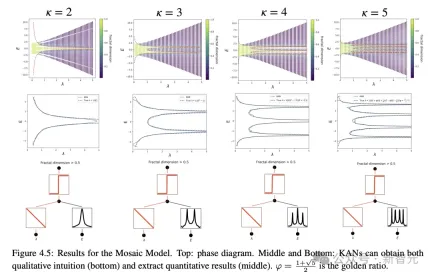
Obviously, KAN has become a powerful assistant and important collaborator for scientists.

In summary, KAN will be a useful model/tool ​​for AI Science thanks to the advantages of accuracy, parameter efficiency, and interpretability.

In the future, further applications of KAN in the scientific field have yet to be explored.

The above is the detailed content of MLP was killed overnight! MIT Caltech and other revolutionary KANs break records and discover mathematical theorems that crush DeepMind. For more information, please follow other related articles on the PHP Chinese website!