
Principal component analysis (PCA) is a dimensionality reduction technique that projects high-dimensional data to new coordinates in a low-dimensional space by identifying and interpreting the directions of maximum variance in the data. As a linear method, PCA is able to extract the most important features, thereby helping us better understand the data. By reducing the dimensionality of data, PCA can reduce storage space and computational complexity while retaining the key information of the data. This makes PCA a powerful tool for processing large-scale data and exploring data structures.
The basic idea of PCA is to find a new set of orthogonal axes, namely principal components, through linear transformation, which is used to extract the most important information in the data. These principal components are linear combinations of the original data, chosen so that the first principal component explains the greatest variance in the data, the second principal component explains the second greatest variance, and so on. In this way, we can use fewer principal components to represent the original data, thereby reducing the dimensionality of the data while retaining most of the information. Through PCA, we can better understand and explain the structure and changes of the data.
Principal component analysis (PCA) is a commonly used dimensionality reduction technique that uses eigenvalue decomposition to calculate principal components. In this process, you first need to calculate the covariance matrix of the data, and then find the eigenvectors and eigenvalues of this matrix. Eigenvectors represent principal components, and eigenvalues measure the importance of each principal component. By projecting the data into a new space defined by feature vectors, dimensionality reduction of the data can be achieved, thereby reducing the number of features and retaining most of the information.
Principal component analysis (PCA) is usually explained using the eigendecomposition of the covariance matrix, but can also be implemented through the singular value decomposition (SVD) of the data matrix. In short, we can use SVD of the data matrix for dimensionality reduction.
Specifically:
SVD stands for Singular Value Decomposition, which states that any matrix A can be decomposed into A=USV^T. This means that matrices U and V are orthogonal matrices and their column vectors are chosen from the eigenvectors of matrices A and A^T. Matrix S is a diagonal matrix whose diagonal elements are the square roots of the eigenvalues of matrices A and A^T.
Principal component analysis (PCA) has many uses in practical applications. For example, in image data, PCA can be used to reduce the dimensionality for easier analysis and classification. Additionally, PCA can be used to detect patterns in gene expression data and find outliers in financial data.
Principal component analysis (PCA) can not only be used for dimensionality reduction, but can also be used to visualize high-dimensional data by reducing it to two or three dimensions, helping to explore and understand the data structure.
The above is the detailed content of PCA: reveals the main features of the data. For more information, please follow other related articles on the PHP Chinese website!
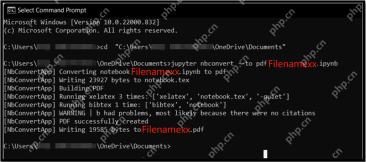 5 Methods to Convert .ipynb Files to PDF- Analytics VidhyaApr 15, 2025 am 10:06 AM
5 Methods to Convert .ipynb Files to PDF- Analytics VidhyaApr 15, 2025 am 10:06 AMJupyter Notebook (.ipynb) files are widely used in data analysis, scientific computing, and interactive encoding. While these Notebooks are great for developing and sharing code with other data scientists, sometimes you need to convert it into a more generally readable format, such as PDF. This guide will walk you through the various ways to convert .ipynb files to PDFs, as well as tips, best practices, and troubleshooting suggestions. Table of contents Why convert .ipynb to PDF? How to convert .ipynb files to PDF Using the Jupyter Notebook UI Using nbconve
 A Comprehensive Guide on LLM Quantization and Use CasesApr 15, 2025 am 10:02 AM
A Comprehensive Guide on LLM Quantization and Use CasesApr 15, 2025 am 10:02 AMIntroduction Large Language Models (LLMs) are revolutionizing natural language processing, but their immense size and computational demands limit deployment. Quantization, a technique to shrink models and lower computational costs, is a crucial solu
 A Comprehensive Guide to Selenium with PythonApr 15, 2025 am 09:57 AM
A Comprehensive Guide to Selenium with PythonApr 15, 2025 am 09:57 AMIntroduction This guide explores the powerful combination of Selenium and Python for web automation and testing. Selenium automates browser interactions, significantly improving testing efficiency for large web applications. This tutorial focuses o
 A Guide to Understanding Interaction TermsApr 15, 2025 am 09:56 AM
A Guide to Understanding Interaction TermsApr 15, 2025 am 09:56 AMIntroduction Interaction terms are incorporated in regression modelling to capture the effect of two or more independent variables in the dependent variable. At times, it is not just the simple relationship between the control
 Swiggy's Hermes: AI Solution for Seamless Data-Driven DecisionsApr 15, 2025 am 09:50 AM
Swiggy's Hermes: AI Solution for Seamless Data-Driven DecisionsApr 15, 2025 am 09:50 AMSwiggy's Hermes: Revolutionizing Data Access with Generative AI In today's data-driven landscape, Swiggy, a leading Indian food delivery service, is leveraging the power of generative AI through its innovative tool, Hermes. Designed to accelerate da
 Gaurav Agarwal's Blueprint for Success with RagaAI - Analytics VidhyaApr 15, 2025 am 09:46 AM
Gaurav Agarwal's Blueprint for Success with RagaAI - Analytics VidhyaApr 15, 2025 am 09:46 AMThis episode of "Leading with Data" features Gaurav Agarwal, CEO and founder of RagaAI, a company focused on ensuring the reliability of generative AI. Gaurav discusses his journey in AI, the challenges of building dependable AI systems, a
 Grok 2 Image Generator: Shown Angry Elon Musk Holding AR15Apr 15, 2025 am 09:45 AM
Grok 2 Image Generator: Shown Angry Elon Musk Holding AR15Apr 15, 2025 am 09:45 AMGrok-2: Unfiltered AI Image Generation Sparks Ethical Debate Elon Musk's xAI has launched Grok-2, a powerful AI model boasting enhanced chat, coding, and reasoning capabilities, alongside a controversial unfiltered image generator. This release has
 Top 10 GitHub Repositories to Master Statistics - Analytics VidhyaApr 15, 2025 am 09:44 AM
Top 10 GitHub Repositories to Master Statistics - Analytics VidhyaApr 15, 2025 am 09:44 AMStatistical Mastery: Top 10 GitHub Repositories for Data Science Statistics is fundamental to data science and machine learning. This article explores ten leading GitHub repositories that provide excellent resources for mastering statistical concept


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Dreamweaver CS6
Visual web development tools

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

SublimeText3 Linux new version
SublimeText3 Linux latest version

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

WebStorm Mac version
Useful JavaScript development tools





