
Bayesian deep learning is a method that combines Bayesian statistics and deep learning techniques. It aims to solve existing problems in deep learning, such as overfitting, parameter uncertainty, and insufficient data. This article will introduce the principles, applications and algorithms of Bayesian deep learning in detail.
1. Principle
Conventional deep learning models mainly use the maximum likelihood estimation method to estimate parameters, that is, through maximization training Likelihood function on the data set to find optimal parameter values. However, this method cannot provide quantification of uncertainty about parameters, nor can it effectively deal with problems such as overfitting. In contrast, Bayesian deep learning adopts a Bayesian approach to model model parameters, enabling the quantification of parameter uncertainty and obtaining model confidence. By introducing a prior probability distribution, Bayesian deep learning can update and estimate parameters by calculating a posterior probability distribution, thereby obtaining more accurate and reliable results. This method not only provides parameter uncertainty measures, but also effectively solves the overfitting problem and provides more flexibility and interpretability for model selection and uncertainty inference. The emergence of Bayesian deep learning has brought
to the field of deep learning. Bayesian deep learning combines the prior distribution of model parameters and the likelihood function of training data to calculate parameters. The posterior distribution of , thus obtaining the confidence of the model. In the inference phase, the distribution of model predictions is calculated through the posterior distribution, quantifying the uncertainty of the model. During the training phase, estimates of parameters are obtained by maximizing the posterior distribution. Different from traditional point estimation, parameter estimation in Bayesian deep learning is a distribution that can reflect the uncertainty of parameters. This method can more accurately represent the confidence of the model and provide more reliable prediction results.
2. Application
Bayesian deep learning has been applied in many fields. Here are some typical applications.
1. Image classification
The application of Bayesian deep learning in image classification has received widespread attention. Traditional deep learning models are prone to overfitting when dealing with small samples, while Bayesian deep learning can reduce the overfitting problem of the model by introducing a prior distribution. At the same time, Bayesian deep learning can quantify the confidence of the model, so that more reliable decisions can be made when the model is uncertain.
2. Natural Language Processing
Bayesian deep learning is also widely used in natural language processing. For example, Bayesian deep learning can be used to improve tasks such as machine translation, text classification, sentiment analysis, and more. By introducing prior distribution and posterior distribution, Bayesian deep learning can better deal with the uncertainty and ambiguity problems existing in language data.
3. Reinforcement learning
Bayesian deep learning is also used in reinforcement learning. Reinforcement learning is a method of learning how to make the best decisions through trial and error. Bayesian deep learning can be used to model the uncertainty problem in reinforcement learning, thereby better solving the exploration-exploitation dilemma in reinforcement learning.
3. Algorithm
There are two main algorithms for Bayesian deep learning: variational inference and Markov chain Monte Carlo (MCMC) method.
1. Variational inference
Variational inference is a method of solving Bayesian deep learning by approximating the posterior distribution. Variational inference decomposes the posterior distribution into a tractable distribution family, and then finds the distribution closest to the posterior distribution in this distribution family. The advantage of variational inference is that it is fast in calculation, but some accuracy may be lost due to the use of approximate posterior distributions.
2. Markov Chain Monte Carlo (MCMC) method
MCMC method is a method to simulate the posterior distribution through random sampling Methods. The MCMC method constructs a Markov chain so that the stationary distribution of the chain is the posterior distribution. This Markov chain is then simulated by sampling to obtain an approximation of the posterior distribution. The advantage of the MCMC method is that it can obtain accurate posterior distribution, but the calculation speed is slow.
In addition to the above two methods, there are other Bayesian deep learning algorithms, such as Gibbs sampling, black box variational inference, etc.
The above is the detailed content of Introduction to Bayesian Deep Learning. For more information, please follow other related articles on the PHP Chinese website!
 Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AM
Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AMThis article explores the growing concern of "AI agency decay"—the gradual decline in our ability to think and decide independently. This is especially crucial for business leaders navigating the increasingly automated world while retainin
 How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AM
How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AMEver wondered how AI agents like Siri and Alexa work? These intelligent systems are becoming more important in our daily lives. This article introduces the ReAct pattern, a method that enhances AI agents by combining reasoning an
 Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM
Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM"I think AI tools are changing the learning opportunities for college students. We believe in developing students in core courses, but more and more people also want to get a perspective of computational and statistical thinking," said University of Chicago President Paul Alivisatos in an interview with Deloitte Nitin Mittal at the Davos Forum in January. He believes that people will have to become creators and co-creators of AI, which means that learning and other aspects need to adapt to some major changes. Digital intelligence and critical thinking Professor Alexa Joubin of George Washington University described artificial intelligence as a “heuristic tool” in the humanities and explores how it changes
 Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AM
Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AMLangChain is a powerful toolkit for building sophisticated AI applications. Its agent architecture is particularly noteworthy, allowing developers to create intelligent systems capable of independent reasoning, decision-making, and action. This expl
 What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AM
What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AMRadial Basis Function Neural Networks (RBFNNs): A Comprehensive Guide Radial Basis Function Neural Networks (RBFNNs) are a powerful type of neural network architecture that leverages radial basis functions for activation. Their unique structure make
 The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AM
The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AMBrain-computer interfaces (BCIs) directly link the brain to external devices, translating brain impulses into actions without physical movement. This technology utilizes implanted sensors to capture brain signals, converting them into digital comman
 Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AM
Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AMThis "Leading with Data" episode features Ines Montani, co-founder and CEO of Explosion AI, and co-developer of spaCy and Prodigy. Ines offers expert insights into the evolution of these tools, Explosion's unique business model, and the tr
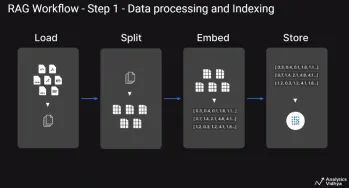 A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AM
A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AMThis article explores Retrieval Augmented Generation (RAG) systems and how AI agents can enhance their capabilities. Traditional RAG systems, while useful for leveraging custom enterprise data, suffer from limitations such as a lack of real-time dat


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Dreamweaver CS6
Visual web development tools

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

Zend Studio 13.0.1
Powerful PHP integrated development environment

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool






