 Technology peripherals
Technology peripherals AI
AI The difference between linear support vector machines and general vector machines
The difference between linear support vector machines and general vector machinesThe difference between linear support vector machines and general vector machines

Linear support vector machine (LSVM) and general support vector machine (SVM) are machine learning models commonly used for classification and regression. Their core idea is to separate different classes or solve regression problems by finding the optimal hyperplane in the data space. Although they both fall under the category of support vector machines, there are some differences between them. LSVM is a support vector machine model based on a linear kernel function, which assumes that the data can be well segmented by a linear hyperplane. Its advantage is that it is computationally simple and easy to interpret, but it can only handle linearly separable problems and may not work well for nonlinear data. SVM is a more general support vector machine model that uses kernel functions to map data into a high-dimensional feature space, thereby converting nonlinear problems into linearly separable problems. SVM can use different kernel functions to adapt to different types of data, such as polynomial kernels, Gaussian kernels, etc. This makes SVM perform better when dealing with nonlinear problems, but the computational complexity is relatively
1. Model form
LSVM is a The decision boundary of a linear classifier is a hyperplane, expressed as w^Tx b=0. Among them, w is the normal vector and b is the offset. Unlike LSVM, SVM not only supports linear classification, but also uses kernel functions to map data into high-dimensional space for nonlinear classification or regression. The decision boundary of SVM can be expressed as\sum_{i=1}^n\alpha_i y_i K(x_i,x) b=0. In this equation, \alpha_i is the Lagrange multiplier, y_i is the label, and K(x_i,x) is the output of the kernel function.
2. Model optimization
There are some differences between LSVM and SVM in model optimization. The goal of LSVM is to maximize the margin, that is, to maximize the distance from the decision boundary to the nearest sample point of each category. The goal of SVM is to simultaneously minimize the loss function and maximize the margin. SVM usually uses Hinge Loss as the loss function, which can punish misclassified samples.
3. Solved problem type
LSVM can only perform linear classification or regression. For nonlinear problems, nonlinear transformation or kernel function is required. to process. SVM can not only handle linear problems, but also use kernel functions to map data into a higher-dimensional space for nonlinear classification or regression. This is one of the reasons why SVM is more flexible than LSVM.
4. Model complexity
Since SVM supports the use of kernel functions for nonlinear classification or regression, its model complexity is generally higher than that of LSVM higher. When using the kernel function, the data is mapped into a high-dimensional space, causing the model to process more features. This also leads to higher training time and computing resource consumption of SVM, which may pose challenges to the processing of large-scale data sets.
5. Robustness to outliers
LSVM is more sensitive to outliers because its goal is to maximize the interval, while Outliers may have a larger impact on the interval. SVM is relatively robust. It uses Hinge Loss to punish misclassified samples, so the impact on some outliers will be relatively small.
In general, LSVM and SVM are both variants of support vector machines and can be used for classification and regression problems. Compared with LSVM, SVM is more flexible, can handle nonlinear problems, and is relatively robust. However, the model complexity of SVM is higher and requires more computing resources and training time. Therefore, in practical applications, it is necessary to select an appropriate model according to the specific situation.
The above is the detailed content of The difference between linear support vector machines and general vector machines. For more information, please follow other related articles on the PHP Chinese website!
 Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AM
Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AMThis article explores the growing concern of "AI agency decay"—the gradual decline in our ability to think and decide independently. This is especially crucial for business leaders navigating the increasingly automated world while retainin
 How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AM
How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AMEver wondered how AI agents like Siri and Alexa work? These intelligent systems are becoming more important in our daily lives. This article introduces the ReAct pattern, a method that enhances AI agents by combining reasoning an
 Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM
Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM"I think AI tools are changing the learning opportunities for college students. We believe in developing students in core courses, but more and more people also want to get a perspective of computational and statistical thinking," said University of Chicago President Paul Alivisatos in an interview with Deloitte Nitin Mittal at the Davos Forum in January. He believes that people will have to become creators and co-creators of AI, which means that learning and other aspects need to adapt to some major changes. Digital intelligence and critical thinking Professor Alexa Joubin of George Washington University described artificial intelligence as a “heuristic tool” in the humanities and explores how it changes
 Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AM
Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AMLangChain is a powerful toolkit for building sophisticated AI applications. Its agent architecture is particularly noteworthy, allowing developers to create intelligent systems capable of independent reasoning, decision-making, and action. This expl
 What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AM
What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AMRadial Basis Function Neural Networks (RBFNNs): A Comprehensive Guide Radial Basis Function Neural Networks (RBFNNs) are a powerful type of neural network architecture that leverages radial basis functions for activation. Their unique structure make
 The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AM
The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AMBrain-computer interfaces (BCIs) directly link the brain to external devices, translating brain impulses into actions without physical movement. This technology utilizes implanted sensors to capture brain signals, converting them into digital comman
 Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AM
Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AMThis "Leading with Data" episode features Ines Montani, co-founder and CEO of Explosion AI, and co-developer of spaCy and Prodigy. Ines offers expert insights into the evolution of these tools, Explosion's unique business model, and the tr
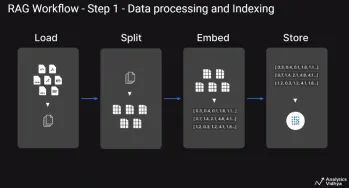 A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AM
A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AMThis article explores Retrieval Augmented Generation (RAG) systems and how AI agents can enhance their capabilities. Traditional RAG systems, while useful for leveraging custom enterprise data, suffer from limitations such as a lack of real-time dat


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Chinese version
Chinese version, very easy to use

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

Notepad++7.3.1
Easy-to-use and free code editor




