Theory and techniques of weight update in neural networks

Weight update in neural network is to adjust the connection weights between neurons in the network through methods such as back propagation algorithm to improve the performance of the network. This article will introduce the concept and method of weight update to help readers better understand the training process of neural networks.
1. Concept
The weights in neural networks are parameters connecting different neurons and determine the strength of signal transmission. Each neuron receives the signal from the previous layer, multiplies it by the weight of the connection, adds a bias term, and is finally activated through the activation function and passed to the next layer. Therefore, the size of the weight directly affects the strength and direction of the signal, which in turn affects the output of the neural network.
The purpose of weight update is to optimize the performance of the neural network. During the training process, the neural network adapts to the training data by continuously adjusting the weights between neurons to improve the prediction ability on the test data. By adjusting the weights, the neural network can better fit the training data, thereby improving the prediction accuracy. In this way, the neural network can more accurately predict the results of unknown data and achieve better performance.
2. Method
Commonly used weight update methods in neural networks include gradient descent, stochastic gradient descent, and batch gradient descent.
Gradient descent method
The gradient descent method is one of the most basic weight update methods. Its basic idea is to calculate the loss function to update the weight. The gradient (that is, the derivative of the loss function with respect to the weight) is used to update the weight to minimize the loss function. Specifically, the steps of the gradient descent method are as follows:
First, we need to define a loss function to measure the performance of the neural network on the training data. Usually, we will choose the mean square error (MSE) as the loss function, which is defined as follows:
MSE=\frac{1}{n}\sum_{i=1} ^{n}(y_i-\hat{y_i})^2
Where, y_i represents the true value of the i-th sample, \hat{y_i} represents the neural network's response to the i-th sample The predicted value of samples, n represents the total number of samples.
Then, we need to calculate the derivative of the loss function with respect to the weight, that is, the gradient. Specifically, for each weight w_{ij} in the neural network, its gradient can be calculated by the following formula:
\frac{\partial MSE}{\partial w_{ij }}=\frac{2}{n}\sum_{k=1}^{n}(y_k-\hat{y_k})\cdot f'(\sum_{j=1}^{m}w_{ij }x_{kj})\cdot x_{ki}
Among them, n represents the total number of samples, m represents the input layer size of the neural network, and x_{kj} represents the kth sample For the jth input feature, f(\cdot) represents the activation function, and f'(\cdot) represents the derivative of the activation function.
Finally, we can update the weights through the following formula:
w_{ij}=w_{ij}-\alpha\cdot\ frac{\partial MSE}{\partial w_{ij}}
Among them, \alpha represents the learning rate, which controls the step size of weight update.
Stochastic gradient descent method
The stochastic gradient descent method is a variant of the gradient descent method. Its basic idea is to randomly select each time A sample is used to calculate the gradient and update the weights. Compared to the gradient descent method, the stochastic gradient descent method can converge faster and be more efficient when processing large-scale data sets. Specifically, the steps of the stochastic gradient descent method are as follows:
First, we need to shuffle the training data and randomly select a sample x_k to calculate the gradient. We can then calculate the derivative of the loss function with respect to the weights via the following formula:
\frac{\partial MSE}{\partial w_{ij}}=2(y_k-\hat {y_k})\cdot f'(\sum_{j=1}^{m}w_{ij}x_{kj})\cdot x_{ki}
where, y_k represents the true value of the k-th sample, \hat{y_k} represents the predicted value of the k-th sample by the neural network.
Finally, we can update the weights through the following formula:
w_{ij}=w_{ij}-\alpha\cdot\ frac{\partial MSE}{\partial w_{ij}}
Among them, \alpha represents the learning rate, which controls the step size of weight update.
Batch gradient descent method
The batch gradient descent method is another variant of the gradient descent method. The basic idea is to use A mini-batch of samples is used to calculate the gradient and update the weights. Compared with gradient descent and stochastic gradient descent, batch gradient descent can converge more stably and is more efficient when processing small-scale data sets. Specifically, the steps of the batch gradient descent method are as follows:
First, we need to divide the training data into several mini-batches of equal size, each mini-batch contains b samples. We can then calculate the average gradient of the loss function against the weights on each mini-batch, which is:
\frac{1}{b}\sum_{k=1}^{ b}\frac{\partial MSE}{\partial w_{ij}}
where b represents the mini-batch size. Finally, we can update the weights through the following formula:
w_{ij}=w_{ij}-\alpha\cdot\frac{1}{b}\sum_{k= 1}^{b}\frac{\partial MSE}{\partial w_{ij}}
Among them, \alpha represents the learning rate, which controls the step size of weight update.
The above is the detailed content of Theory and techniques of weight update in neural networks. For more information, please follow other related articles on the PHP Chinese website!
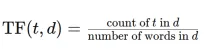 Convert Text Documents to a TF-IDF Matrix with tfidfvectorizerApr 18, 2025 am 10:26 AM
Convert Text Documents to a TF-IDF Matrix with tfidfvectorizerApr 18, 2025 am 10:26 AMThis article explains the Term Frequency-Inverse Document Frequency (TF-IDF) technique, a crucial tool in Natural Language Processing (NLP) for analyzing textual data. TF-IDF surpasses the limitations of basic bag-of-words approaches by weighting te
 Building Smart AI Agents with LangChain: A Practical GuideApr 18, 2025 am 10:18 AM
Building Smart AI Agents with LangChain: A Practical GuideApr 18, 2025 am 10:18 AMUnleash the Power of AI Agents with LangChain: A Beginner's Guide Imagine showing your grandmother the wonders of artificial intelligence by letting her chat with ChatGPT – the excitement on her face as the AI effortlessly engages in conversation! Th
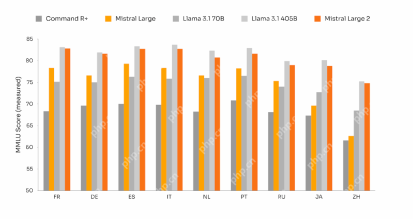 Mistral Large 2: Powerful Enough to Challenge Llama 3.1 405B?Apr 18, 2025 am 10:16 AM
Mistral Large 2: Powerful Enough to Challenge Llama 3.1 405B?Apr 18, 2025 am 10:16 AMMistral Large 2: A Deep Dive into Mistral AI's Powerful Open-Source LLM Meta AI's recent release of the Llama 3.1 family of models was quickly followed by Mistral AI's unveiling of its largest model to date: Mistral Large 2. This 123-billion paramet
 What is Noise Schedules in Stable Diffusion? - Analytics VidhyaApr 18, 2025 am 10:15 AM
What is Noise Schedules in Stable Diffusion? - Analytics VidhyaApr 18, 2025 am 10:15 AMUnderstanding Noise Schedules in Diffusion Models: A Comprehensive Guide Have you ever been captivated by the stunning visuals of digital art generated by AI and wondered about the underlying mechanics? A key element is the "noise schedule,&quo
 How to Build a Conversational Chatbot with GPT-4o? - Analytics VidhyaApr 18, 2025 am 10:06 AM
How to Build a Conversational Chatbot with GPT-4o? - Analytics VidhyaApr 18, 2025 am 10:06 AMBuilding a Contextual Chatbot with GPT-4o: A Comprehensive Guide In the rapidly evolving landscape of AI and NLP, chatbots have become indispensable tools for developers and organizations. A key aspect of creating truly engaging and intelligent chat
 Top 7 Frameworks for Building AI Agents in 2025Apr 18, 2025 am 10:00 AM
Top 7 Frameworks for Building AI Agents in 2025Apr 18, 2025 am 10:00 AMThis article explores seven leading frameworks for building AI agents – autonomous software entities that perceive, decide, and act to achieve goals. These agents, surpassing traditional reinforcement learning, leverage advanced planning and reasoni
 What's the Difference Between Type I and Type II Errors ? - Analytics VidhyaApr 18, 2025 am 09:48 AM
What's the Difference Between Type I and Type II Errors ? - Analytics VidhyaApr 18, 2025 am 09:48 AMUnderstanding Type I and Type II Errors in Statistical Hypothesis Testing Imagine a clinical trial testing a new blood pressure medication. The trial concludes the drug significantly lowers blood pressure, but in reality, it doesn't. This is a Type
 Automated Text Summarization with Sumy LibraryApr 18, 2025 am 09:37 AM
Automated Text Summarization with Sumy LibraryApr 18, 2025 am 09:37 AMSumy: Your AI-Powered Summarization Assistant Tired of sifting through endless documents? Sumy, a powerful Python library, offers a streamlined solution for automatic text summarization. This article explores Sumy's capabilities, guiding you throug


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

SublimeText3 English version
Recommended: Win version, supports code prompts!

SublimeText3 Chinese version
Chinese version, very easy to use

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool






