Detailed explanation of B-tree deletion operation: Detailed illustration of B-tree deletion operation using Python

The B-tree deletion operation needs to consider the location and balance of the node, and underflow is likely to occur. Underflow occurs when a node contains less than the minimum number of child nodes it should hold.

Pictures and text show the principle of B-tree deletion operation

without affecting the balance.

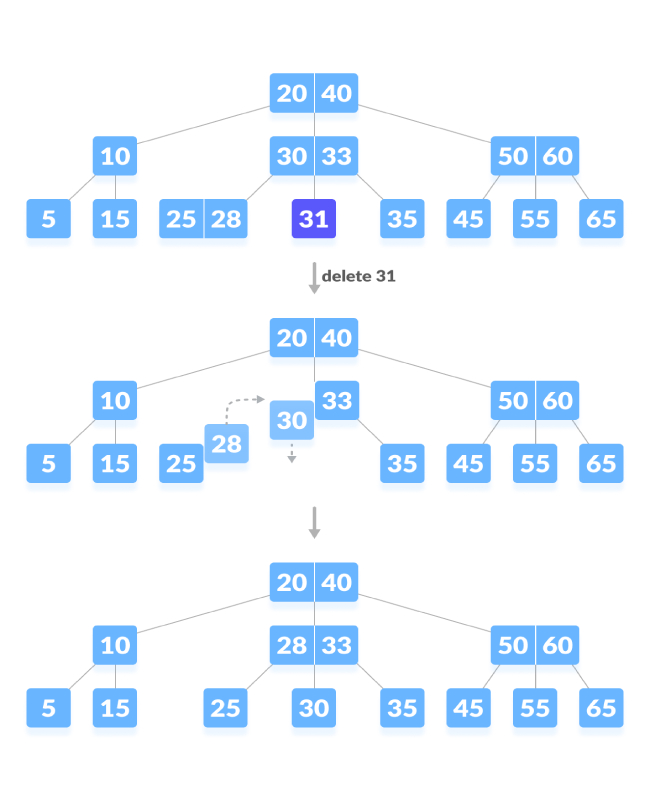
Underflow situation.

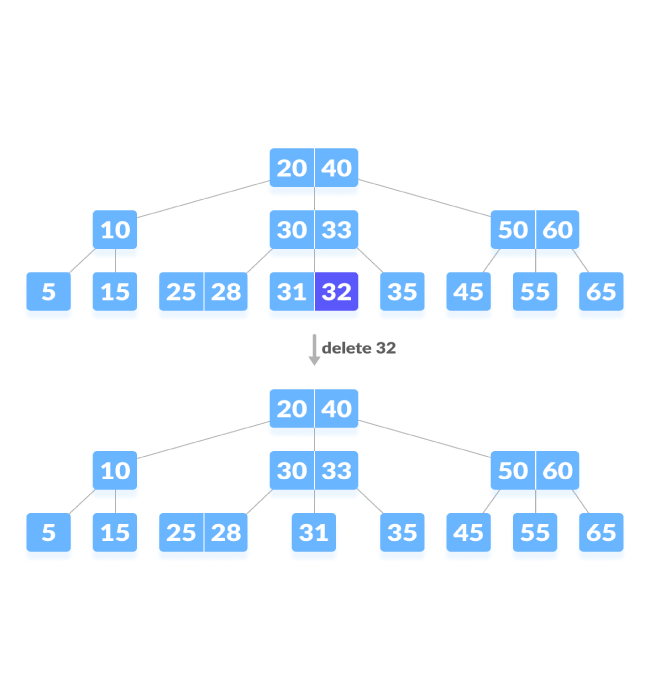
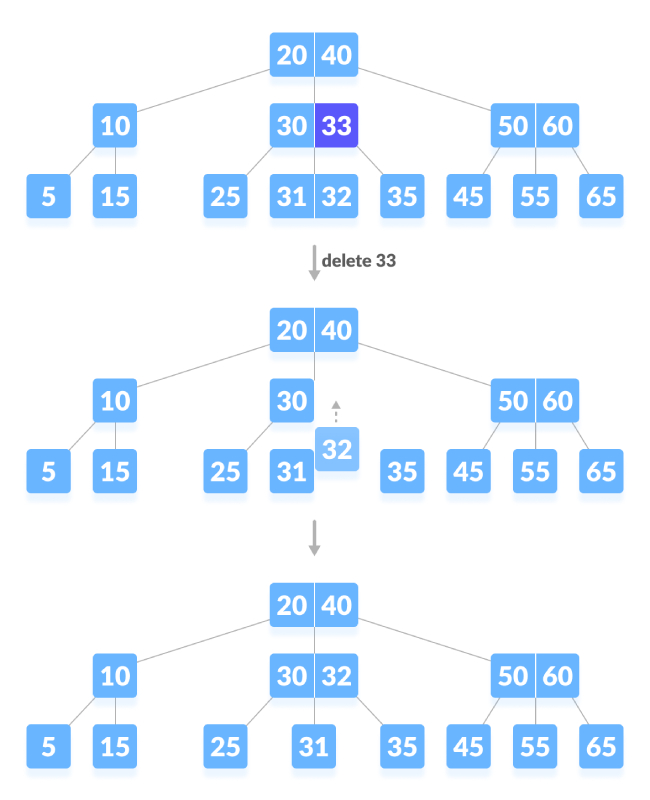
Delete internal nodes.

Python implements B-tree deletion operation

# B树节点
class BTreeNode:
    def __init__(self, leaf=False):
        self.leaf = leaf
        self.keys = []
        self.child = []

class BTree:
    def __init__(self, t):
        self.root = BTreeNode(True)
        self.t = t

    # 插入元素
    def insert(self, k):
        root = self.root
        if len(root.keys) == (2 * self.t) - 1:
            temp = BTreeNode()
            self.root = temp
            temp.child.insert(0, root)
            self.split_child(temp, 0)
            self.insert_non_full(temp, k)
        else:
            self.insert_non_full(root, k)

    def insert_non_full(self, x, k):
        i = len(x.keys) - 1
        if x.leaf:
            x.keys.append((None, None))
            while i >= 0 and k[0] < x.keys[i][0]:
                x.keys[i + 1] = x.keys[i]
                i -= 1
            x.keys[i + 1] = k
        else:
            while i >= 0 and k[0] < x.keys[i][0]:
                i -= 1
            i += 1
            if len(x.child[i].keys) == (2 * self.t) - 1:
                self.split_child(x, i)
                if k[0] > x.keys[i][0]:
                    i += 1
            self.insert_non_full(x.child[i], k)

    # 分开子节点
    def split_child(self, x, i):
        t = self.t
        y = x.child[i]
        z = BTreeNode(y.leaf)
        x.child.insert(i + 1, z)
        x.keys.insert(i, y.keys[t - 1])
        z.keys = y.keys[t: (2 * t) - 1]
        y.keys = y.keys[0: t - 1]
        if not y.leaf:
            z.child = y.child[t: 2 * t]
            y.child = y.child[0: t - 1]

    # 删除节点
    def delete(self, x, k):
        t = self.t
        i = 0
        while i < len(x.keys) and k[0] > x.keys[i][0]:
            i += 1
        if x.leaf:
            if i < len(x.keys) and x.keys[i][0] == k[0]:
                x.keys.pop(i)
                return
            return

        if i < len(x.keys) and x.keys[i][0] == k[0]:
            return self.delete_internal_node(x, k, i)
        elif len(x.child[i].keys) >= t:
            self.delete(x.child[i], k)
        else:
            if i != 0 and i + 2 < len(x.child):
                if len(x.child[i - 1].keys) >= t:
                    self.delete_sibling(x, i, i - 1)
                elif len(x.child[i + 1].keys) >= t:
                    self.delete_sibling(x, i, i + 1)
                else:
                    self.delete_merge(x, i, i + 1)
            elif i == 0:
                if len(x.child[i + 1].keys) >= t:
                    self.delete_sibling(x, i, i + 1)
                else:
                    self.delete_merge(x, i, i + 1)
            elif i + 1 == len(x.child):
                if len(x.child[i - 1].keys) >= t:
                    self.delete_sibling(x, i, i - 1)
                else:
                    self.delete_merge(x, i, i - 1)
            self.delete(x.child[i], k)

    # 删除节点
    def delete_internal_node(self, x, k, i):
        t = self.t
        if x.leaf:
            if x.keys[i][0] == k[0]:
                x.keys.pop(i)
                return
            return

        if len(x.child[i].keys) >= t:
            x.keys[i] = self.delete_predecessor(x.child[i])
            return
        elif len(x.child[i + 1].keys) >= t:
            x.keys[i] = self.delete_successor(x.child[i + 1])
            return
        else:
            self.delete_merge(x, i, i + 1)
            self.delete_internal_node(x.child[i], k, self.t - 1)

    # 删除前节点
    def delete_predecessor(self, x):
        if x.leaf:
            return x.pop()
        n = len(x.keys) - 1
        if len(x.child[n].keys) >= self.t:
            self.delete_sibling(x, n + 1, n)
        else:
            self.delete_merge(x, n, n + 1)
        self.delete_predecessor(x.child[n])

    # 删除继任节点
    def delete_successor(self, x):
        if x.leaf:
            return x.keys.pop(0)
        if len(x.child[1].keys) >= self.t:
            self.delete_sibling(x, 0, 1)
        else:
            self.delete_merge(x, 0, 1)
        self.delete_successor(x.child[0])

    def delete_merge(self, x, i, j):
        cnode = x.child[i]

        if j > i:
            rsnode = x.child[j]
            cnode.keys.append(x.keys[i])
            for k in range(len(rsnode.keys)):
                cnode.keys.append(rsnode.keys[k])
                if len(rsnode.child) > 0:
                    cnode.child.append(rsnode.child[k])
            if len(rsnode.child) > 0:
                cnode.child.append(rsnode.child.pop())
            new = cnode
            x.keys.pop(i)
            x.child.pop(j)
        else:
            lsnode = x.child[j]
            lsnode.keys.append(x.keys[j])
            for i in range(len(cnode.keys)):
                lsnode.keys.append(cnode.keys[i])
                if len(lsnode.child) > 0:
                    lsnode.child.append(cnode.child[i])
            if len(lsnode.child) > 0:
                lsnode.child.append(cnode.child.pop())
            new = lsnode
            x.keys.pop(j)
            x.child.pop(i)

        if x == self.root and len(x.keys) == 0:
            self.root = new

    # 删除同一级的其他子节点
    def delete_sibling(self, x, i, j):
        cnode = x.child[i]
        if i < j:
            rsnode = x.child[j]
            cnode.keys.append(x.keys[i])
            x.keys[i] = rsnode.keys[0]
            if len(rsnode.child) > 0:
                cnode.child.append(rsnode.child[0])
                rsnode.child.pop(0)
            rsnode.keys.pop(0)
        else:
            lsnode = x.child[j]
            cnode.keys.insert(0, x.keys[i - 1])
            x.keys[i - 1] = lsnode.keys.pop()
            if len(lsnode.child) > 0:
                cnode.child.insert(0, lsnode.child.pop())

    # 输出B树
    def print_tree(self, x, l=0):
        print("Level ", l, " ", len(x.keys), end=":")
        for i in x.keys:
            print(i, end=" ")
        print()
        l += 1
        if len(x.child) > 0:
            for i in x.child:
                self.print_tree(i, l)

B = BTree(3)

for i in range(10):
    B.insert((i, 2 * i))

B.print_tree(B.root)
B.delete(B.root, (8,))
print("\n")
B.print_tree(B.root)

The above is the detailed content of Detailed explanation of B-tree deletion operation: Detailed illustration of B-tree deletion operation using Python. For more information, please follow other related articles on the PHP Chinese website!