 Web Front-end
Web Front-end JS Tutorial
JS Tutorial Compare the different approaches of recursive and iterative algorithms in computing transitive closures
Compare the different approaches of recursive and iterative algorithms in computing transitive closures
Explore two different algorithms for transitive closure: recursive algorithm vs iterative algorithm
Transitive closure is an important concept in graph theory, used to describe graphs Reachability relationships between nodes. In a directed graph, if starting from node A, we can reach node B through a series of directed edges, then we say that node A is passed to node B. The purpose of transitive closure is to find the transitive relationship between all nodes and express it in the form of a matrix. This article will explore two different algorithms for transitive closures: recursive and iterative, along with their concrete code examples.
Recursive algorithm is a method of solving problems by calling functions recursively. When solving transitive closures, you can use recursive algorithms to achieve this. The following is a code example of a recursive algorithm:
def transitive_closure_recursive(adjacency_matrix):
"""
递归算法求解传递闭包
Args:
adjacency_matrix: 邻接矩阵
Returns:
transitive_closure: 传递闭包矩阵
"""
n = len(adjacency_matrix) # 图的节点数
transitive_closure = [[0] * n for _ in range(n)] # 初始化传递闭包矩阵
# 递归函数
def dfs(i, j):
transitive_closure[i][j] = 1 # 将节点i传递到节点j标记为1
for k in range(n):
if adjacency_matrix[j][k] and not transitive_closure[i][k]:
dfs(i, k) # 递归调用
# 对每对节点进行遍历
for i in range(n):
for j in range(n):
if adjacency_matrix[i][j] and not transitive_closure[i][j]:
dfs(i, j) # 调用递归函数进行遍历
return transitive_closureThe iterative algorithm is a method of solving problems through iterative loops. When solving transitive closures, iterative algorithms can be used. The following is a code example of the iterative algorithm:
def transitive_closure_iterative(adjacency_matrix):
"""
迭代算法求解传递闭包
Args:
adjacency_matrix: 邻接矩阵
Returns:
transitive_closure: 传递闭包矩阵
"""
n = len(adjacency_matrix) # 图的节点数
transitive_closure = [[0] * n for _ in range(n)] # 初始化传递闭包矩阵
for i in range(n):
for j in range(n):
if adjacency_matrix[i][j]:
transitive_closure[i][j] = 1 # 将直接可达的节点标记为1
# 迭代更新传递闭包矩阵
for k in range(n):
for i in range(n):
for j in range(n):
transitive_closure[i][j] = transitive_closure[i][j] or (transitive_closure[i][k] and transitive_closure[k][j])
return transitive_closureThe above are specific code examples of the recursive algorithm and the iterative algorithm to solve the transitive closure. Both algorithms have their own characteristics: the recursive algorithm has a simple idea, but may be less efficient when processing large-scale graphs; the iterative algorithm is more efficient, but requires more loops and judgment operations. In practical applications, an appropriate algorithm can be selected to solve the transitive closure according to the scale and requirements of the specific problem.
In summary, recursive algorithms and iterative algorithms are two different ways to solve transitive closure problems. Through code examples, we can clearly see the differences and characteristics between them. In practical applications, appropriate algorithms can be selected to handle transitive closures based on specific problems and requirements.
The above is the detailed content of Compare the different approaches of recursive and iterative algorithms in computing transitive closures. For more information, please follow other related articles on the PHP Chinese website!
 Replace String Characters in JavaScriptMar 11, 2025 am 12:07 AM
Replace String Characters in JavaScriptMar 11, 2025 am 12:07 AMDetailed explanation of JavaScript string replacement method and FAQ This article will explore two ways to replace string characters in JavaScript: internal JavaScript code and internal HTML for web pages. Replace string inside JavaScript code The most direct way is to use the replace() method: str = str.replace("find","replace"); This method replaces only the first match. To replace all matches, use a regular expression and add the global flag g: str = str.replace(/fi
 8 Stunning jQuery Page Layout PluginsMar 06, 2025 am 12:48 AM
8 Stunning jQuery Page Layout PluginsMar 06, 2025 am 12:48 AMLeverage jQuery for Effortless Web Page Layouts: 8 Essential Plugins jQuery simplifies web page layout significantly. This article highlights eight powerful jQuery plugins that streamline the process, particularly useful for manual website creation
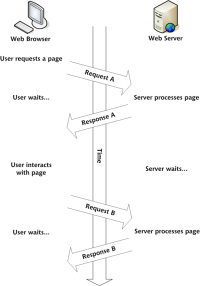 Build Your Own AJAX Web ApplicationsMar 09, 2025 am 12:11 AM
Build Your Own AJAX Web ApplicationsMar 09, 2025 am 12:11 AMSo here you are, ready to learn all about this thing called AJAX. But, what exactly is it? The term AJAX refers to a loose grouping of technologies that are used to create dynamic, interactive web content. The term AJAX, originally coined by Jesse J
 How do I create and publish my own JavaScript libraries?Mar 18, 2025 pm 03:12 PM
How do I create and publish my own JavaScript libraries?Mar 18, 2025 pm 03:12 PMArticle discusses creating, publishing, and maintaining JavaScript libraries, focusing on planning, development, testing, documentation, and promotion strategies.
 Load Box Content Dynamically using AJAXMar 06, 2025 am 01:07 AM
Load Box Content Dynamically using AJAXMar 06, 2025 am 01:07 AMThis tutorial demonstrates creating dynamic page boxes loaded via AJAX, enabling instant refresh without full page reloads. It leverages jQuery and JavaScript. Think of it as a custom Facebook-style content box loader. Key Concepts: AJAX and jQuery
 10 jQuery Fun and Games PluginsMar 08, 2025 am 12:42 AM
10 jQuery Fun and Games PluginsMar 08, 2025 am 12:42 AM10 fun jQuery game plugins to make your website more attractive and enhance user stickiness! While Flash is still the best software for developing casual web games, jQuery can also create surprising effects, and while not comparable to pure action Flash games, in some cases you can also have unexpected fun in your browser. jQuery tic toe game The "Hello world" of game programming now has a jQuery version. Source code jQuery Crazy Word Composition Game This is a fill-in-the-blank game, and it can produce some weird results due to not knowing the context of the word. Source code jQuery mine sweeping game
 How to Write a Cookie-less Session Library for JavaScriptMar 06, 2025 am 01:18 AM
How to Write a Cookie-less Session Library for JavaScriptMar 06, 2025 am 01:18 AMThis JavaScript library leverages the window.name property to manage session data without relying on cookies. It offers a robust solution for storing and retrieving session variables across browsers. The library provides three core methods: Session
 jQuery Parallax Tutorial - Animated Header BackgroundMar 08, 2025 am 12:39 AM
jQuery Parallax Tutorial - Animated Header BackgroundMar 08, 2025 am 12:39 AMThis tutorial demonstrates how to create a captivating parallax background effect using jQuery. We'll build a header banner with layered images that create a stunning visual depth. The updated plugin works with jQuery 1.6.4 and later. Download the


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

SublimeText3 Chinese version
Chinese version, very easy to use





