 Technology peripherals
Technology peripherals AI
AI Over 70% mAP for the first time! GeMap: Local high-precision map SOTA refreshed again
Over 70% mAP for the first time! GeMap: Local high-precision map SOTA refreshed againOver 70% mAP for the first time! GeMap: Local high-precision map SOTA refreshed again
Written in front&The author’s personal understanding
Building vectorized high-precision maps based on sensor data in real time is crucial for downstream tasks such as prediction and planning, and can effectively make up for offline high-precision maps The disadvantage of poor real-time performance of the map. With the development of deep learning, online vectorized high-precision map construction has gradually emerged, and representative works such as HDMapNet, MapTR, etc. have emerged one after another. However, existing online vectorized high-precision map construction methods lack exploration of the geometric properties of map elements (including the shape of elements, vertical, parallel and other geometric relationships).
The geometric properties of vectorized high-precision maps
The vectorized high-precision maps highly abstract the elements on the road and represent each map element as a two-dimensional point sequence. The design of urban roads has specific specifications. For example, in most cases, pedestrian crosswalks are square rectangle or parallelogram; in road sections that do not involve diverging and merging, two adjacent Lanes are parallel to each other. Different elements in high-precision maps also have many similar characteristics. These common-sense rules are abstracted into Geometric properties of high-precision maps, including the shape of map elements (rectangle, parallelogram , straight lines, etc.), or associations between different map elements (parallel, vertical, etc.). Geometric properties strongly constrain the representation of map elements. If you fully understand the geometric properties of online model construction, you can get more accurate results.
Propose the importance of geometric representation for high-precision maps
Although in theory it is still possible for existing models to learn the geometric properties of map elements, however, the geometric properties The characteristics determine that at least under traditional design, the model is not easy to learn.
- Invariance of geometric properties
When the central vehicle drives straight on the road, changes lanes, or turns, (in the vehicle coordinate system ) The absolute coordinates of map elements are constantly changing. The shape of crosswalks, lanes, road boundaries, etc. will not change; similarly, the parallel relationship between lanes will not change. The geometric properties of map elements are objective, and one of its important characteristics is invariance. More specifically, it is rigid invariance (remaining invariant to rotation and translation transformation). Previous work, whether using simple polyline representation or polynomial curves with control points (such as Bezier curves, piecewise Bezier curves), was based on absolute coordinates, and in absolute coordinates Basic end-to-end optimization. The optimization goal based on absolute coordinates itself does not have rigid invariance, so it is difficult to expect that the local optimal solution that the model falls into contains an understanding of geometric properties. Therefore, a representation that can fully characterize the geometric properties and have certain invariance is necessary.
 Figure 1. Example of geometric invariance.
Figure 1. Example of geometric invariance.
When the vehicle turns right, the absolute coordinates will change significantly. The image on the right shows a corresponding real-life scenario.
- Diversity of Geometric Properties
Furthermore, despite strong prior knowledge, the geometric properties of roads are still diverse. These various geometric properties can generally be divided into two categories, one is about the geometric shape of a single map element, and the other is about the geometric association of different map elements. Due to the diversity of geometric properties, it is impossible to exhaustively and manually convert geometric properties into constraints, so we prefer that the model can autonomously learn a variety of geometric properties end-to-end.
Design of GeMap
Geometric representation
In view of the above two problems, we first improve the representation method. We hope to introduce a good geometric representation in addition to the traditional representation based on absolute coordinates, which needs to satisfy:
- Be able to describe the shape of map elements
- Be able to depict the association between map elements
- rigidityinvariance
to ensure translation invariance, we used a relative quantity, that is, the offset vector between points; to further ensure rotation invariance, we chose the length of the offset vector , and different Angle between offset vectors. These two - length and angle - form the basis of the geometric representation we propose. In addition, in order to better distinguish and describe shapes and relate two different types of geometric properties, we further refined the design according to the principle of simplicity:
In order to describe the shape, weCalculate the offset vector between adjacent points in a single map element, and calculate the length of the offset vector and the angle between adjacent offset vectors. This representation uniquely identifies any polyline/polygon. Examples of two images are shown below:

Please look at Figure 2, which shows the representation of geometric shapes
For a rectangle, it can be described by using a right angle and two pairs of equal sides; for a straight line, all included angles are 0 Degree or 180.
To characterize the association, similarly, we first consider the distance between any two points. However, if the angle is calculated for all point-to-point offset vectors, the complexity of the representation is too high and the computational cost is unaffordable. Specifically, assuming that there are a total of map elements, and each element is represented by a point, the amount of data for all angles will reach (when taking 1000, assuming that each angle data is a 32-bit floating point number, such a representation is only The space occupied will reach TB level). In fact, this is not necessary for normal vertical, parallel, etc. relationships. Therefore, we first calculate the offsets within the elements, and then only calculate the angle between the two offsets as part of the geometric representation. This simplified association representation retains the ability to describe parallel, vertical and other relationships, while the corresponding data amount is only (roughly 4MB under the aforementioned conditions). For ease of understanding, we also provide some examples:

Figure 3. Geometric association representation.
The parallel relationship and the perpendicular relationship are expressed by the angle between the offset vector being 0 degrees or 90 degrees; the distance between the two points can reflect the width information of the lane to a certain extent
To optimize the representation of geometric shapes and associations, we adopt the simplest approach, directly calculate the geometric representation of predictions and labels, and then use the norm as the optimization target :

Here and represent the length and angle calculated based on the label respectively, and and represent the length and angle calculated based on the prediction. A trick is used when dealing with included angles: directly calculating the angle involves a discontinuous arctan function, which will encounter difficulties during optimization (there is a vanishing gradient problem near ±90 degrees), so what we actually compare is the included angle The cosine and sine values of It also represents the robustness of the loss to rotation and translation transformation
 Geometric decoupling attention
Geometric decoupling attention
In self-attention, all queries (that is, "points") interact equally with each other. However, the shape of the map elements corresponds to a group of queries. The interaction between these groups becomes a liability when perceiving the shape of elements. On the contrary, when perceiving the relationship between elements, shape also becomes a redundant factor
. This means thatdecoupling the perception of shape and association may lead to better results
.To decouple geometry and association processing, we adopt a two-step self-attention process: Each map element consists of
queries, Attention is performed within this
- query to process geometric shapes
- Supplement the attention relationship across elements to process geometric associationsGeometric solution Coupled attention can be more vividly represented by the following figure. Our implementation is relatively simple, directly using masks to control the scope of attention. Since these two types of attention are complementary, with reasonable implementation, the time complexity may be equivalent to performing a single self-attention
Figure 4. Geometry Decoupling attention.
The left side is the shape attention carried out within a single element, and the right side is the associated attention carried out between elements. 
Experimental results
We conducted a large number of experiments on nuScenes and Argoverse 2 data sets. Both are commonly used large-scale autonomous driving data sets, and both provide map annotations.Main results
We conducted three sets of experiments on nuScenes. First, we use a relatively pure combination of objective functions, including only geometric losses and other necessary losses (such as point-to-point distance, edge direction, classification). This combination aims to highlight the importance of the geometric properties we propose. value without overly pursuing SOTA results. The results show that our method improves mAP compared to MapTR in this case. To explore the limits of GeMap, we also add some auxiliary objectives, including segmentation and depth estimation. In this case, we also achieved SOTA results (mAP improvement). It is worth noting that achieving such an improvement does not require sacrificing too much inference speed. Finally, we also tried to introduce additional LiDAR modal inputs. With the help of additional modal inputs, the performance of GeMap was further improved

Similarly, in the Argoverse 2 data set On the above, our method also achieved very outstanding results.

The rewritten content is: ablation experiment
The further rewritten content on nuScenes is: ablation experiment proof The value of geometric loss and geometrically decoupled attention. Interestingly, as we expected, using geometric loss directly will lead to a decrease in model performance. We believe that this is because the structural coupling of shape and association processing makes it difficult for the model to optimize the geometric representation; and after combining with the geometric decoupling attention, the geometric loss plays its due role (From "Euclidean Loss" to "Full").

More results
In addition, we also performed a visual analysis of nuScenes. It can be seen from the visualization results that GeMap is not only robust in handling rotation and translation, but also shows certain advantages in solving occlusion problems, as shown in the figure below. Challenging map elements are marked with orange boxes in the figure

Figure 5. Visual comparison results.
In the experimental results on rainy days, we also quantitatively verified the robustness of occlusion (see the table below). This is because rain naturally blocks the camera

This can be explained by the model learning geometric properties and therefore being able to better guess map elements even when there are occlusions. For example, if the model understands the shape of the lane lines, then it only needs to "see" part of it to estimate the rest; the model understands the parallel relationship between the lane lines, or the width characteristics of the lane, so even if one of them is blocked , and can also guess the occluded part based on the parallel relationship and width factors
Summary
We pointed out the geometric properties of the map elements and their importance for online vectorization The value of high-precision map construction. Based on this, we propose a powerful method to initially verify this value. In addition, GeMap's robustness to occlusion may indicate the idea of using geometric properties to deal with occlusion in other autonomous driving tasks (such as detection, occupancy prediction, etc.) - because both vehicles and roads have relatively standardized geometric properties. . Of course, our method itself has much to explore further. For example, can geometric elements of different complexity be adaptively described using different points? Is it possible to understand the geometric representation from a probabilistic perspective and make it more robust to noise? Because we have simplified the element association, is there a better representation of geometric association? These are all directions for further optimization.

The content that needs to be rewritten is: https://mp.weixin.qq.com/s/BoxlskT68Kjb07mfwQ7Swg link
The above is the detailed content of Over 70% mAP for the first time! GeMap: Local high-precision map SOTA refreshed again. For more information, please follow other related articles on the PHP Chinese website!
 Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AM
Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AMSince 2008, I've championed the shared-ride van—initially dubbed the "robotjitney," later the "vansit"—as the future of urban transportation. I foresee these vehicles as the 21st century's next-generation transit solution, surpas
 Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AM
Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AMRevolutionizing the Checkout Experience Sam's Club's innovative "Just Go" system builds on its existing AI-powered "Scan & Go" technology, allowing members to scan purchases via the Sam's Club app during their shopping trip.
 Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AM
Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AMNvidia's Enhanced Predictability and New Product Lineup at GTC 2025 Nvidia, a key player in AI infrastructure, is focusing on increased predictability for its clients. This involves consistent product delivery, meeting performance expectations, and
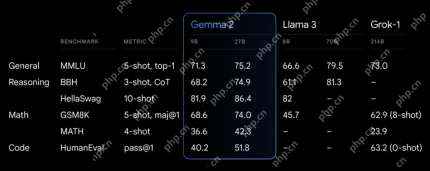 Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AM
Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AMGoogle's Gemma 2: A Powerful, Efficient Language Model Google's Gemma family of language models, celebrated for efficiency and performance, has expanded with the arrival of Gemma 2. This latest release comprises two models: a 27-billion parameter ver
 The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AM
The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AMThis Leading with Data episode features Dr. Kirk Borne, a leading data scientist, astrophysicist, and TEDx speaker. A renowned expert in big data, AI, and machine learning, Dr. Borne offers invaluable insights into the current state and future traje
 AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AM
AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AMThere were some very insightful perspectives in this speech—background information about engineering that showed us why artificial intelligence is so good at supporting people’s physical exercise. I will outline a core idea from each contributor’s perspective to demonstrate three design aspects that are an important part of our exploration of the application of artificial intelligence in sports. Edge devices and raw personal data This idea about artificial intelligence actually contains two components—one related to where we place large language models and the other is related to the differences between our human language and the language that our vital signs “express” when measured in real time. Alexander Amini knows a lot about running and tennis, but he still
 Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AM
Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AMCaterpillar's Chief Information Officer and Senior Vice President of IT, Jamie Engstrom, leads a global team of over 2,200 IT professionals across 28 countries. With 26 years at Caterpillar, including four and a half years in her current role, Engst
 New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AM
New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AMGoogle Photos' New Ultra HDR Tool: A Quick Guide Enhance your photos with Google Photos' new Ultra HDR tool, transforming standard images into vibrant, high-dynamic-range masterpieces. Ideal for social media, this tool boosts the impact of any photo,


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

SublimeText3 Linux new version
SublimeText3 Linux latest version





