Label acquisition problem in unsupervised learning

The label acquisition problem in unsupervised learning requires specific code examples
With the development of big data and machine learning, unsupervised learning has become a solution to various problems in the real world. One of the important ways to solve the problem. Unlike supervised learning, unsupervised learning does not require pre-labeled training data, but instead learns and predicts by automatically discovering patterns and regularities from the data. However, in practical applications, some label or category information is often needed to analyze and evaluate data. Therefore, how to obtain labels in unsupervised learning becomes a key issue.
The label acquisition problem in unsupervised learning involves two aspects: clustering and dimensionality reduction. Clustering is the process of classifying similar samples into the same category or group, which can help us discover hidden structures in the data; dimensionality reduction maps high-dimensional data to a low-dimensional space to better visualize and understand the data. . This article will introduce the label acquisition issues in clustering and dimensionality reduction respectively, and give specific code examples.
1. Label acquisition problem in clustering
Clustering is an unsupervised learning method that groups similar samples into different categories or groups. In clustering, it is often necessary to compare the clustering results with the real labels to evaluate the quality and effectiveness of the clustering. But in unsupervised learning, it is difficult to obtain real label information for evaluation. Therefore, we need some techniques and methods to obtain the labels of clusters.
A common method is to use external indicators, such as ARI (Adjusted Rand Index) and NMI (Normalized Mutual Information), to measure the similarity between the clustering results and the real labels. These metrics can be calculated through the metrics module in the sklearn library. The following is an example of using the K-means clustering algorithm to obtain labels:
from sklearn.cluster import KMeans
from sklearn import metrics
# 加载数据
data = load_data()
# 初始化聚类器
kmeans = KMeans(n_clusters=3)
# 进行聚类
labels = kmeans.fit_predict(data)
# 计算外部指标ARI和NMI
true_labels = load_true_labels()
ari = metrics.adjusted_rand_score(true_labels, labels)
nmi = metrics.normalized_mutual_info_score(true_labels, labels)
print("ARI: ", ari)
print("NMI: ", nmi)In the above code, the data is first loaded through the load_data() function, then the KMeans algorithm is used for clustering, and the fit_predict() method is used to obtain the clusters. Class label. Finally, load the real label information through the load_true_labels() function, and use adjusted_rand_score() and normalized_mutual_info_score() to calculate the ARI and NMI indicators.
In addition to external metrics, we can also use internal metrics to evaluate the quality of clustering. Internal metrics are calculated within the data and do not require real label information. Commonly used internal indicators include Silhouette Coefficient and DB Index (Davies-Bouldin Index). The following is an example of using silhouette coefficients to obtain labels:
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# 加载数据
data = load_data()
# 初始化聚类器
kmeans = KMeans(n_clusters=3)
# 进行聚类
labels = kmeans.fit_predict(data)
# 计算轮廓系数
silhouette_avg = silhouette_score(data, labels)
print("Silhouette Coefficient: ", silhouette_avg)In the above code, the data is first loaded through the load_data() function, then the KMeans algorithm is used for clustering, and the fit_predict() method is used to obtain the clustering labels. . Finally, the silhouette coefficient is calculated through silhouette_score().
2. Label acquisition issues in dimensionality reduction
Dimensionality reduction is a method of mapping high-dimensional data to low-dimensional space, which can help us better understand and visualize the data. In dimensionality reduction, some label or category information is also needed to evaluate the effect of dimensionality reduction.
A commonly used dimensionality reduction algorithm is Principal Component Analysis (PCA), which maps the original data to a new coordinate system through linear transformation. When using PCA for dimensionality reduction, we can use the label information of the original data to evaluate the effect of dimensionality reduction. The following is an example of using PCA to obtain labels:
from sklearn.decomposition import PCA # 加载数据和标签 data, labels = load_data_and_labels() # 初始化PCA模型 pca = PCA(n_components=2) # 进行降维 reduced_data = pca.fit_transform(data) # 可视化降维结果 plt.scatter(reduced_data[:, 0], reduced_data[:, 1], c=labels) plt.show()
In the above code, the data and labels are first loaded through the load_data_and_labels() function, then the PCA algorithm is used for dimensionality reduction, and the fit_transform() method is used to obtain the dimensionality reduction result. Finally, the scatter() function is used to visualize the dimensionality reduction results, where the label information is represented by color.
It should be noted that obtaining labels in unsupervised learning is an auxiliary means, which is different from label acquisition in supervised learning. Label acquisition in unsupervised learning is more for evaluating and understanding the effect of the model, and is not necessary in practical applications. Therefore, when choosing a tag acquisition method, you need to make a flexible choice based on specific application scenarios.
The above is the detailed content of Label acquisition problem in unsupervised learning. For more information, please follow other related articles on the PHP Chinese website!
 Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AM
Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AMThis article explores the growing concern of "AI agency decay"—the gradual decline in our ability to think and decide independently. This is especially crucial for business leaders navigating the increasingly automated world while retainin
 How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AM
How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AMEver wondered how AI agents like Siri and Alexa work? These intelligent systems are becoming more important in our daily lives. This article introduces the ReAct pattern, a method that enhances AI agents by combining reasoning an
 Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM
Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM"I think AI tools are changing the learning opportunities for college students. We believe in developing students in core courses, but more and more people also want to get a perspective of computational and statistical thinking," said University of Chicago President Paul Alivisatos in an interview with Deloitte Nitin Mittal at the Davos Forum in January. He believes that people will have to become creators and co-creators of AI, which means that learning and other aspects need to adapt to some major changes. Digital intelligence and critical thinking Professor Alexa Joubin of George Washington University described artificial intelligence as a “heuristic tool” in the humanities and explores how it changes
 Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AM
Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AMLangChain is a powerful toolkit for building sophisticated AI applications. Its agent architecture is particularly noteworthy, allowing developers to create intelligent systems capable of independent reasoning, decision-making, and action. This expl
 What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AM
What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AMRadial Basis Function Neural Networks (RBFNNs): A Comprehensive Guide Radial Basis Function Neural Networks (RBFNNs) are a powerful type of neural network architecture that leverages radial basis functions for activation. Their unique structure make
 The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AM
The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AMBrain-computer interfaces (BCIs) directly link the brain to external devices, translating brain impulses into actions without physical movement. This technology utilizes implanted sensors to capture brain signals, converting them into digital comman
 Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AM
Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AMThis "Leading with Data" episode features Ines Montani, co-founder and CEO of Explosion AI, and co-developer of spaCy and Prodigy. Ines offers expert insights into the evolution of these tools, Explosion's unique business model, and the tr
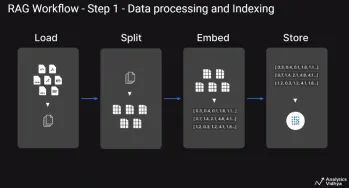 A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AM
A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AMThis article explores Retrieval Augmented Generation (RAG) systems and how AI agents can enhance their capabilities. Traditional RAG systems, while useful for leveraging custom enterprise data, suffer from limitations such as a lack of real-time dat


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

Dreamweaver Mac version
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

WebStorm Mac version
Useful JavaScript development tools





