Find the shortest path between any two nodes using the Floyd-Warshal algorithm

C There is a macro, which is defined as a piece of code or an expected value, and it will be reused whenever the user needs it. The Floyd-Walshall algorithm is the process of finding the shortest path between all pairs of vertices in a given weighted graph. The algorithm follows a dynamic programming approach to find the minimum weight graph.

Let us understand the meaning of Freud-Walschal algorithm through diagrams -

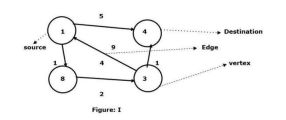
Taking vertex 1 as the source and vertex 4 as the destination, find the shortest path between them.

We have seen that there are two paths that can be connected to target vertex 4.

• 1 -> 4 – The edge has a weight of 5

• 1 -> 8 -> 3 -> 4 – The edge weight (1 2 1) is 4.

In the given graph I, we see the smallest edge connecting two vertices. So here the path between vertex 8 and vertex 3 connecting vertex 1 to vertex 4 and the edge is 4. On the other hand, there is a directed edge between vertex 1 and vertex 4, and the edge weight is 5.

Now we compare two weights, namely 4 and 5. Therefore, here 4 is the minimum weight of the graph calculated according to the Floyd Warshall algorithm.

In this article, we will use Floyd Warshall algorithm to find the shortest path between any two given nodes.

grammar

The following syntax is used in the program -

data_type[][] array_name;

parameter

data_type[][] - The data type mentioned by the user. The first array represents rows and the second array represents columns. So, this represents a two-dimensional array.

array_name - The name given to the array.

algorithm

• We will start the program with the header file 'iostream' and define the macro position as 'INF' (infinity) because later it will satisfy the two-dimensional Array matrices and if-else statements.

• Next, we create a global function definition named 'printPath' and accepts three parameters, namely 'parent[]', 'i' and 'j' Verify that the path exists.

• Then we start the main function and store the value ‘4’ into the variable ‘V’, which represents the number of vertices. Second, store the value in the form of an adjacency matrix into the variable 'dist[V][V]'. As we know, dist[i][j] represents a 2D matrix, which defines the weight of the edge from 'i' to 'j', By storing the adjacency matrix.

• Next, we are initializing the 2D array for the variable 'parent', and the size is [V][V].

In this variable we use to display each pair of vertices 'i' and 'j' w.r.t 'parent[i][j]' .

• By using two nested for loops, we will find the shortest path. The first for loop iterates over the rows in the matrix. Then, iterate over the columns in the matrix through the second for loop and then we will check the following condition using if-else statement -

• If (dist[i][j] != INF && i != j) { The Chinese translation of parent[i][j] = i;}

  is: parent[i][j] = i;}

  In the if statement, we use the 'and' (&&) operator to express two conditions. If both conditions are met, then 'i' will be stored in 'parent[i ][j]', thereby verifying that the path exists.

• other{ The Chinese translation of parent[i][j] = -1;}

  is: parent[i][j] = -1;}

  In the else statement, we initialize "-1" to "parent[i][j]" to verify that the path does not exist.

• Now we start with three nested for loops and apply k vertices in the range 0 to V-1, with the help of this range, our shortest distance and the path will be updated. In the third nested loop we use the following condition like

if (dist[i][j] < dist[i][k] + dist[k][j]){
   dist[i][j] = dist[i][k] + dist[k][j]; 
   parent[i][j] = parent[k][j];	
}

Here K is updating the row and column parts of the two-dimensional array matrix, which verifies the newly updated shortest path and distance.

• Next, we print out the shortest distance and path of all vertex pairs by giving the following conditions

• By using two nested for loops, we print the shortest distance and path.

• By using the if statement under the second for loop, we will check if dist[i][j] is equal to infinity. If it is found to be infinity, print "INF", otherwise print the shortest path.

• Finally, we call the function named 'printPath()' by passing three parameters (parent[i], i, and j.

Example

In this program, we will use Floyd Warshall algorithm to calculate the shortest path between any two nodes.

#include <iostream> 
using namespace std; 
#define INF 1000000000 // Infinity

void printPath(int parent[], int i, int j) {
   if (i == j) 
      cout << i << " "; 
   else if (parent[j] == -1) 
     cout << "No path exists"; 
   else
   { 
      printPath(parent, i, parent[j]); 
      cout << j << " "; 
   }
} 

int main() 
{
   int V = 4; 
   // V represent number of vertices
   int dist[V][V] = {{0, 2, INF, 4}, 
      {6, 0, 5, 3}, 
      {INF, 10, 0, 1}, 
      {7, 9, 8, 0}}; 
   // Represent the graph using adjacency matrix

   // Apply the Floyd Warshall algorithm to find the shortest paths
   int parent[V][V];
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      {
         if (dist[i][j] != INF && i != j)
         parent[i][j] = i;
         else
         parent[i][j] = -1;
      }
   }
   // update the path and distance using the k vertex range from 0 to V-1.
   for (int k = 0; k < V; k++) 
   { 
      for (int i = 0; i < V; i++) 
      { 
         for (int j = 0; j < V; j++) 
         { 
            if (dist[i][j] > dist[i][k] + dist[k][j]) 
            {
               dist[i][j] = dist[i][k] + dist[k][j];
               parent[i][j] = parent[k][j];	
            }
         }
      }
   }

   // Print shortest distances and paths between all pairs of vertices
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      { 
         cout << "The Shortest distance between " << i << " and " << j << " is ";
         if (dist[i][j] == INF) 
            cout << "INF "; 
         else
            cout << dist[i][j] << " ";

         cout << "and the shortest path is:- ";
         printPath(parent[i], i, j);
         cout << endl;
      } 
   } 

   return 0; 
}

输出

The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 
The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 
The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 
The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 
The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 
The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 
The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 
The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 
The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 
The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 
The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 
The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 
The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 
The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 
The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 
The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3 

结论

我们学习了使用Floyd Warshall算法找到任意两个节点之间的最短路径的概念。我们使用邻接矩阵作为程序的输入，通过它我们找到了最短路径和距离。此外，为了更新路径和距离，我们使用了k个顶点来更新行和列。在我们的日常生活中，我们在谷歌地图上搜索最短路线或路径，从一个起点到目的地。

The above is the detailed content of Find the shortest path between any two nodes using the Floyd-Warshal algorithm. For more information, please follow other related articles on the PHP Chinese website!