Home >Backend Development >C++ >What is the area of a circle within a rectangle inscribed in a semicircle?
What is the area of a circle within a rectangle inscribed in a semicircle?
- 王林forward
- 2023-09-13 08:45:212051browse
A circle inscribed in a rectangle is tangent to the longer side of the rectangle, that is, the length is tangent to the circle.
A rectangle inscribed in a semicircle touches two points on the arc of the semicircle. The width of the rectangle is equal to the diameter of the circle.
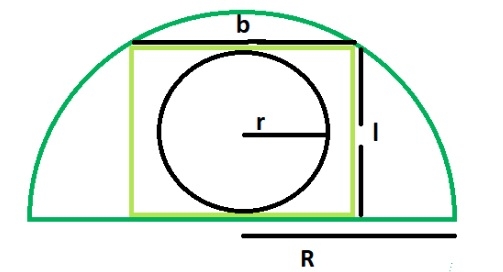
If R is the radius of the semicircle.
The length of the rectangle = √2R/2
The width of the rectangle = R/√2
Inscribed circle The radius of is
r = b/2 = R/2√2
Using this formula we can calculate The area of a circle inscribed in a rectangle inscribed in a semicircle,
area = (π*r2) = π*R/8
Example
Demonstration
#include <stdio.h>
int main() {
float a = 5;
float area = 3.14 * a/ 8;
printf("The area of the circle inscribed in a rectangle inscribed in a semicircle of radius %f is %f", a , area);
return 0;
}Output
The area of the circle inscribed in a rectangle inscribed in a semicircle of radius 5.00000 is 1.962500
The above is the detailed content of What is the area of a circle within a rectangle inscribed in a semicircle?. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- Html easily implements rounded rectangle example
- Introduction to the method of using Path to draw basic graphics such as circles, rectangles, ellipses, triangles, etc. in Android development Canvas
- What should I do if the eraser circle in PS disappears?
- Use js to quickly find the area of a triangle
- How to find the area of a circle in JavaScript

