The number of isosceles triangles in a binary tree

Binary tree is a data structure in which each node can have up to two child nodes. These children are called left children and right children respectively. Suppose we are given a parent array representation, you have to use it to create a binary tree. A binary tree may have several isosceles triangles. We have to find the total number of possible isosceles triangles in this binary tree.

In this article, we will explore several techniques to solve this problem in C.

Understanding Questions

Gives you a parent array. You have to represent it in the form of a binary tree so that the array index forms the value of the tree node and the value in the array gives the parent node of that particular index.

Please note that -1 is always the root parent node. Given below is an array and its binary tree representation.

Parent array = [0, -1, 3, 1, 1, 2, 2, 3, 4, 4]

Binary tree -

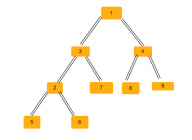
In any binary tree, we can have three types of isosceles triangles -

• Left Isosceles Triangle − In this triangle, the vertex is a left The child node of the parent node, and the vertices forming the base (both sides of the isosceles triangle) are the left child nodes of the vertex. Child nodes can be direct or indirect. In the tree above, we have two such isosceles triangles - (2, 6, 3), (3, 7, 1).

• Right Isosceles Triangle − In this triangle, the vertex is rightChildren of the parent, while the vertices forming the base are the right children of the vertices. Children can be direct or indirect. In the tree above, we have only one such isosceles triangle (4, 1, 8).

• Balanced Isosceles Triangle − In this triangle, the vertices forming the base are the left and right child nodes of the vertex node. In the tree above, we have five such isosceles triangles (1, 3, 4), (3, 2, 7), (4, 8, 9), (2, 5, 6), (1, 2, 9)

Therefore, for the above binary tree, we have a total of 8 isosceles triangles.

Traversal using depth-first search

Depth First Search (DFS) is a method of traversing all nodes of a tree in a depth manner. It starts at the root node, moves to each branch, and then backtracks.

• First, we use DFS to traverse each node of the binary tree and convert it into a graph so that each node is represented as adjacent to each other. This makes traversal easier.

• For each node, we check whether it has child nodes. After checking, we use the sort(node[x].begin(), node[x].end()) function to sort them.

• Next, we check whether the current node is the left or right successor of its corresponding parent node. We use the DFS function recursively on all nodes of the binary tree.

• If the current node has two children (either directly or indirectly), we check the possibility that an isosceles triangle exists by calculating the edges between them. We will find the edges between them through the graph function given in the code below.

• Finally, we calculate the total number of isosceles triangles by adding up all possible triangles in different positions.

Example

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;

#define MAX int(1e5)
vector < int > * node;
int right_down[MAX];
int right_up[MAX];
int left_down[MAX];
int left_up[MAX];

// DFS traversal over a node
void DFS(int x, int * parent) {
   // Check if adjacent nodes are present for node x
   if (node[x].size() != 0)
      sort(node[x].begin(), node[x].end());

   // Check whether the node has a parent node
   if (parent[x] != -1) {
      int indexOfParent = parent[x];
      int childrenCount = node[indexOfParent].size();

      if (childrenCount > 1) {
         int parentFirstChild = node[indexOfParent][0];

         // Check if current node is left node of the parent
         if (x == parentFirstChild) {
            right_up[x] += right_up[indexOfParent] + 1;
            // Check if current node is right node of the parent  
         } else {
            left_up[x] += left_up[indexOfParent] + 1;
         }
      } else {
         right_up[x] += right_up[indexOfParent] + 1;
      }
   }

   // Iterate over children of current node  
   for (int i = 0; i < node[x].size(); ++i) {
      int y = node[x][i];
      DFS(y, parent);

      // left child of current node
      if (i == 0) {
         left_down[x] += left_down[y] + 1;
      }
      // right child of current node
      else {
         right_down[x] += right_down[y] + 1;
      }
   }
}

int graph(int * parent, int N) {
   int rootNode;
   node = new vector < int > [N];

   for (int i = 0; i < N; ++i) {
      if (parent[i] != -1) {
         node[parent[i]].push_back(i);
      } else {
         rootNode = i;
      }

      left_up[i] = 0;
      right_up[i] = 0;
      left_down[i] = 0;
      right_down[i] = 0;
   }
   return rootNode;
}

int main() {
   int N = 10;
   int parent[] = { 0, -1, 3, 1, 1, 2, 2, 3, 4, 4 };
   int rootNode = graph(parent, N);
   DFS(rootNode, parent);
   int count = 0;
   // Counting the total isosceles triangles
   for (int i = 0; i < N; ++i) {
      count += min(right_down[i], right_up[i]);
      count += min(left_down[i], left_up[i]);
      count += min(left_down[i], right_down[i]);
   }
   cout << "Number of isosceles triangles in the binary tree are " <<
      count;
   return 0;
}

Output

Number of isosceles triangles in the binary tree are 8

in conclusion

We have discussed how to find the total number of equilateral triangles in a binary tree when given a parent array. We can achieve this by using depth-first search, which allows us to traverse a binary tree.

The above is the detailed content of The number of isosceles triangles in a binary tree. For more information, please follow other related articles on the PHP Chinese website!