Home >Technology peripherals >AI >How does the thinking chain release the hidden capabilities of language models? The latest theoretical research reveals the mystery behind it
How does the thinking chain release the hidden capabilities of language models? The latest theoretical research reveals the mystery behind it
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBforward
- 2023-06-03 16:49:211190browse
One of the most mysterious phenomena in the emergence of large models is Chain of Thought Tips (CoT), which has shown amazing results especially in solving mathematical reasoning and decision-making problems. How important is CoT? What is the mechanism behind its success? In this article, several researchers from Peking University prove that CoT is indispensable in realizing large language model (LLM) inference, and reveal how CoT can unleash the huge potential of LLM from a theoretical and experimental perspective.
Recent research has found that Chain of Thought prompting (CoT) can significantly improve the performance of large language models (LLM), especially for processing complex problems involving mathematics or reasoning. Task. But despite much success, the mechanisms behind CoTs and how to unlock the potential of LLMs remain elusive.
Recently, a new study from Peking University revealed the mystery behind CoT from a theoretical perspective.

## Paper link: https://arxiv.org/abs/2305.15408
The large language model based on Transformer has become a common model in natural language processing and has been widely used in various tasks. Mainstream large models are usually implemented based on the autoregressive paradigm. Specifically, various tasks (such as text translation, text generation, question answering, etc.) can be uniformly regarded as sequence generation problems, in which the input of the question and the description of the question are encoded together into a word (token) sequence, called a prompt (prompt); the answer to the question can be transformed into the task of conditionally generating subsequent words based on the prompt.


However, although CoT has achieved remarkable performance in a large number of experiments, the theoretical mechanism behind it remains a mystery. On the one hand, do large models indeed have inherent theoretical flaws in directly answering questions about mathematics, reasoning, etc.? On the other hand, why can CoT improve the capabilities of large models on these tasks? This paper answers the above questions from a theoretical perspective.
Specifically, researchers study CoT from the perspective of model expression ability: For mathematical tasks and general decision-making tasks, this article studies the Transformer model based on autoregression in the following two Expressive ability in terms of: (1) directly generating answers, and (2) using CoT to generate complete solution steps.
CoT is the key to solving mathematical problems
Large models represented by GPT-4 have demonstrated astonishing mathematical capabilities. For example, it can correctly solve most high school math problems and has even become a research assistant for mathematicians.
In order to study the mathematical capabilities of large models, this article selected two very basic but core mathematical tasks: arithmetic and equations (the following figure shows the input of these two tasks output example). Since they are fundamental components for solving complex mathematical problems, by studying these two core mathematical problems, we can gain a deeper understanding of the capabilities of large models on general mathematical problems.

The researchers first explored whether Transformer could output answers to the above questions without outputting intermediate steps. They considered an assumption that is very consistent with reality - a log-precision Transformer, that is, each neuron of the Transformer can only represent a floating-point number of limited precision (precision is log n bits), where n is the maximum length of the sentence. This assumption is very close to reality, for example in GPT-3 the machine precision (16 or 32 bits) is usually much smaller than the maximum output sentence length (2048).
Under this assumption, the researchers proved a core impossible result: For an autoregressive Transformer model with a constant layer and a width of d, the direct output The answer is to solve the above two mathematical problems by using a very large model width d. Specifically, d needs to grow larger than the polynomial as the input length n grows.
The essential reason for this result is that there is no efficient parallel algorithm for the above two problems, so Transformer, as a typical parallel model, cannot solve them. The article uses circuit complexity theory in theoretical computer science to rigorously prove the above theorem.
So, what if the model does not output the answer directly, but outputs the intermediate derivation steps in the form of the figure above? The researchers further proved through construction that When the model can output intermediate steps, a fixed-size (not dependent on the input length n) autoregressive Transformer model can solve the above two mathematical problems.
Comparing the previous results, it can be seen that adding CoT greatly improves the expression ability of large models. The researchers further gave an intuitive understanding of this: This is because the introduction of CoT will continuously feed back the generated output words to the input layer, which greatly increases the effective depth of the model, making it proportional to the output length of CoT, thus greatly The parallel complexity of Transformer has been greatly improved.
CoT is the key to solving general decision-making problems
In addition to mathematical problems, researchers further considered CoT’s ability to solve general tasks. Starting from the decision-making problem, they considered a general framework for solving decision-making problems, called dynamic programming.
The basic idea of dynamic programming (DP) is to decompose a complex problem into a series of small-scale sub-problems that can be solved in sequence. The decomposition of the problem ensures that there is significant interrelation (overlap) between the various sub-problems, so that each sub-problem can be solved efficiently using the answers to the previous sub-problems.
The longest ascending subsequence (LIS) and the solution of the edit distance (ED) are two famous DP problems proposed in the book "Introduction to Algorithms". The following table lists these Aggregation functions of state space,transition functions for two problems.

##The researchers proved that the autoregressive Transformer model can solve the sub-problem as follows The sequence outputs a complete dynamic programming thinking chain, so that correct answers can be output for all tasks that can be solved with dynamic programming. Likewise, the researchers further demonstrated that generative thought chains are necessary: for many difficult dynamic programming problems, a constant-layer, polynomial-sized Transformer model cannot directly output the correct answer. The article gives a counterexample to the problem of context-free grammar membership testing. Experiment
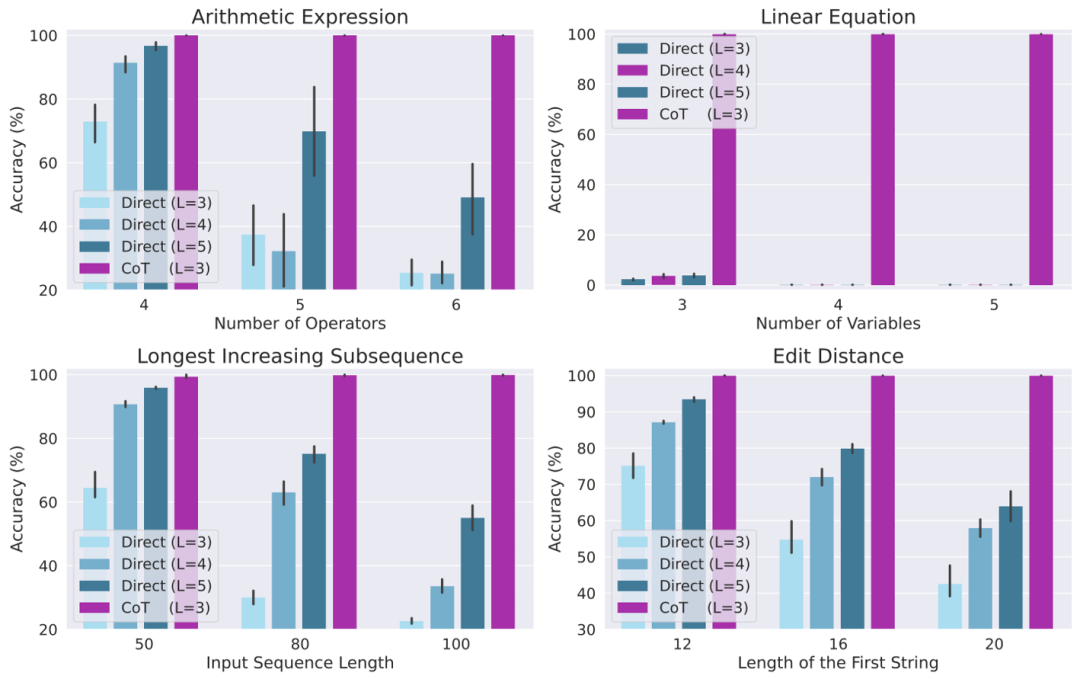
The researchers finally designed a large number of experiments to verify the above theory, considering four different tasks: evaluating arithmetic expressions, solving linear equations, and solving Longest rising subsequence and solving edit distance.
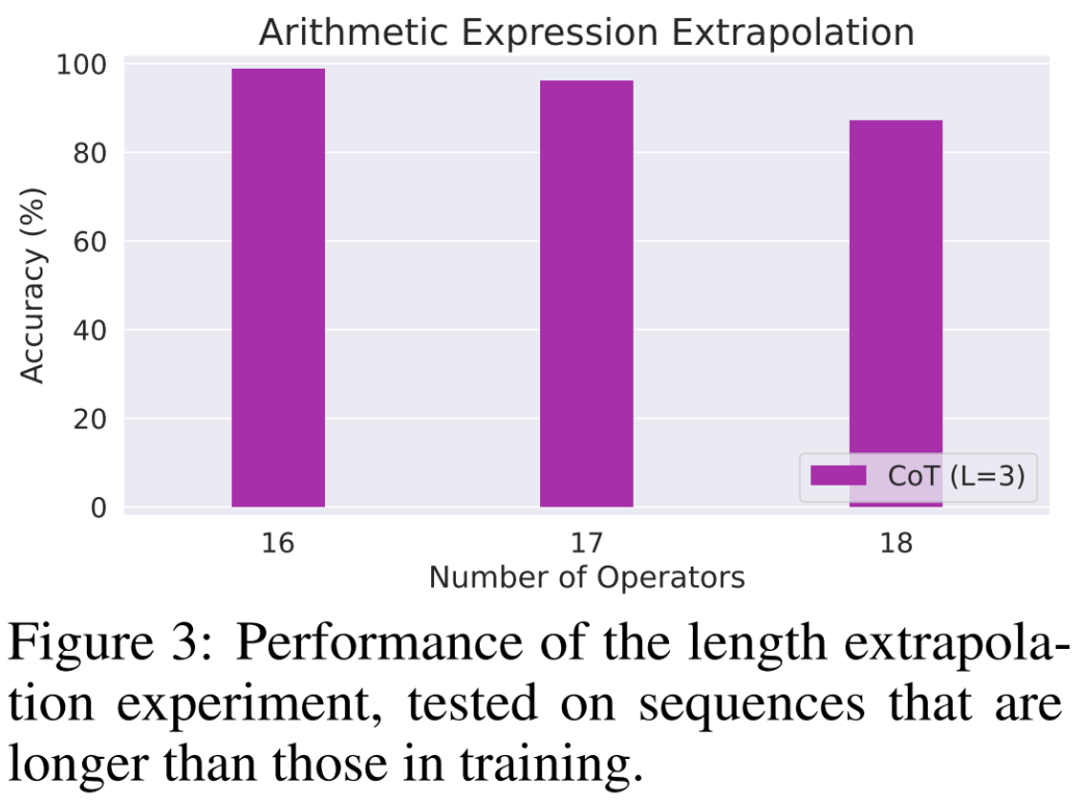
Experimental results show that when trained using CoT data, a 3-layer autoregressive Transformer model has been able to achieve almost perfect performance on all tasks. However, directly outputting the correct answer performs poorly on all tasks (even with deeper models). This result clearly demonstrates the ability of the Autoregressive Transformer to solve a variety of complex tasks and demonstrates the importance of CoT in solving these tasks.
The above is the detailed content of How does the thinking chain release the hidden capabilities of language models? The latest theoretical research reveals the mystery behind it. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- Technology trends to watch in 2023
- How Artificial Intelligence is Bringing New Everyday Work to Data Center Teams
- Can artificial intelligence or automation solve the problem of low energy efficiency in buildings?
- OpenAI co-founder interviewed by Huang Renxun: GPT-4's reasoning capabilities have not yet reached expectations
- Microsoft's Bing surpasses Google in search traffic thanks to OpenAI technology

