Example analysis of indexes and algorithms of Mysql Innodb storage engine

1. Overview

If there are too few indexes, the query efficiency will be low; if there are too many indexes, program performance will be affected, and the use of indexes should be consistent with the actual situation.
Innodb supports indexes including:

• Full text search, using inverted index

• Hash index, adaptive, no human intervention , created based on the clustered index page in the buffer pool, and the entire table will not be hashed, so index creation is very fast.

• B tree index, an index in the traditional sense, is currently the most effective and commonly used index in relational databases.

The B tree cannot locate the specific row record on the table, but returns the page where the row record is located; finally, it is stored in the memory based on the slot information and the row record header. next record information for precise positioning.

2. Data structure and algorithm

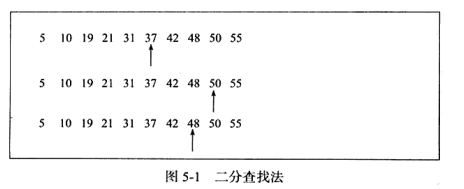
1. Binary search

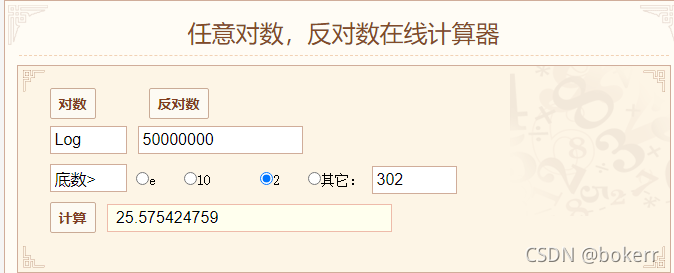
Binary search can only be used to search a set of ordered linear data, taking the median value each time , small forward, large backward. The time complexity of finding the number 48 in an ordered array is log N, as shown in the figure below.

2. Binary search tree and balanced binary tree

1) Binary search tree

Binary search tree refers to, In a binary tree, it is satisfied that: the left child node of any node is smaller than itself, and the right child node of any node is greater than itself is a binary search tree.

Ordinary binary trees cannot guarantee O(logN) access time, because in extreme cases, it can even degenerate into a linked list.

When a set of ordered data is constructed in order to build a binary tree, then a linked list is obtained. At this time, the time complexity becomes: O(N)

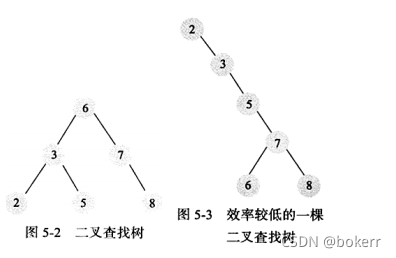
2) Balanced binary tree

A balanced binary tree is similar to a binary search tree, but adds a restriction: the height of the left and right subtrees of each node differs by at most 1. In the process of building a binary tree, if this condition is violated, it can be solved by appropriate rotation.

The balanced binary tree guarantees a time complexity of: O(logN)

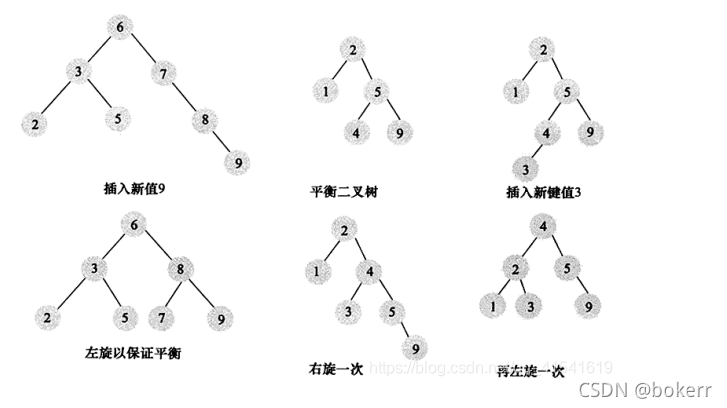
Although it can guarantee an access time of O(logN), it is not suitable Used for database indexing:

When the amount of data is very large, the height of the binary tree will increase rapidly (for example, 1024 is equal to the 10th power of 2), so log(N) is also very significant.

Performing disk IO multiple times is because the leaf nodes of the binary tree can only accommodate one piece of data, which is its most unfavorable feature. However, in actual applications, frequent disk reads will be disastrous compared to the time it takes the CPU to execute instructions. Therefore, binary trees are not suitable for database indexing.

For mechanical hard disks, the access time depends on the disk speed and head movement time, which are all completed by the mechanical structure. Compared with the electrical signal instructions executed in the CPU, the speed must be very different.

10 million data, if a balanced binary tree is used (the worst time bound is 1.44 * logN), even if the worst time bound is not taken, the final calculation based on log(N) is about 24, then it needs to be carried out 24 disk IO times, this is obviously not possible.

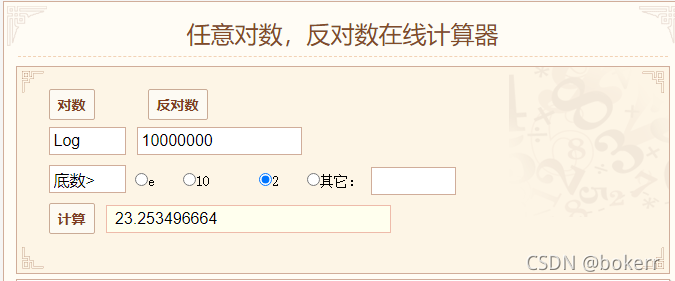
[The tree height is the logarithmic value rounded up, for example: log3 = 1.58, the tree height is 2;]

3. B-tree

Due to the limitations of balanced binary trees, B-trees need to be introduced.

B tree is a balanced search tree specially designed for disks or other direct access auxiliary devices. In the B tree, all record nodes are stored sequentially in the leaves of the same layer according to the size of the key value. Nodes are linked by each leaf node pointer.

1. Complete definition of B-tree

An M-order B-tree needs to satisfy the following properties:

All the following definitions regarding the division of two numbers , if it is not divisible, round it up instead of discarding the decimal places. (Except for deducing inequalities in the case)

1) Data items must exist on leaf nodes

2) Non-leaf nodes store M-1 keywords to indicate the search direction; keyword i represents The smallest keyword in the i 1th subtree of the non-leaf node; assuming a 5-order B-tree, then it has 5 - 1 = 4 keywords.

3) B-tree either has only one leaf node as the root node (without any child nodes); if it has child nodes, its number of nodes must belong to the set: {2~M};

4) Except for the root, the number of child nodes of all non-leaf nodes must satisfy that they belong to the set: { M/2, M };

5) All leaves are at the same depth, and the data items of the leaf nodes are The number must belong to the set: { L/2, L };

2. Selected cases of M and L

Assume that the total length of all fields does not exceed 500 bytes, with a 50-byte primary key For example, simulate and derive the B-tree, including the space occupied by the row record itself

It is known that all row records will consume some bytes to record row information: such as variable length fields, row record headers, transaction IDs, rollback pointers, etc.

create table context(
	id  varchar(50) primary key,
	name varchar(50) not null,
	description varchar(360)  
);

A leaf node represents a data page, and the selection of M and L values ​​is closely related to it. Assume that the data page size is: P/byte (taking the MySQL discussed in this article as an example, the size of a data page is 16K, which is 16384 bytes.)

On non-leaf nodes: the key of the B-tree is the primary key. In this example, it is assumed that the primary key is 50 bytes, and the key of the M-order B-tree is M -1 , occupying: 50 * (M - 1) bytes of space;

plus its branch pointer pointing to M child nodes, assuming that each branch pointer occupies 4 bytes of storage; then a non In leaf nodes, the total space consumption is: 50 * (M - 1) 4 * M = 54M - 50 bytes.

When using MySQL, and assuming that the primary key is 50 bytes, the inequality is established: 54M - 50

On the leaf node, the maximum capacity of each row defined in the known table is: 500 bytes. At this time, the following expression is established: L * 500

As shown below, there are 5000W data at this time and the tree height is greater than 3, which means that we only need up to 4 disk IOs to find the data.

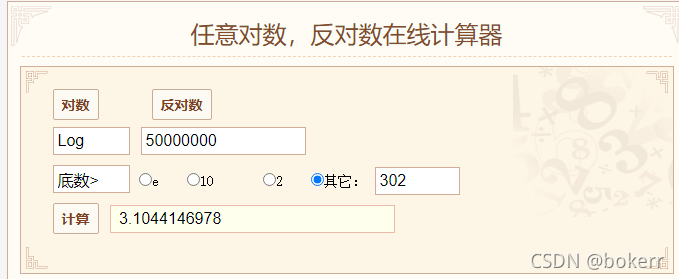
Refer to the figure below, the worst time bound of the balanced binary tree is: 1.44 * logN = 25.58 * 1.44 = 36.83; that is to say, if 5000W data uses a balanced binary tree, the worst time limit of the tree In the worst case, there will be more than 36 disk IO times, and at least 26 disk IO times.

The picture shows a 5-order ordinary B-tree (M = 5), where each node has a maximum of 5 values ​​(L = 5); M and L are not Must be equal, as in the above analysis: M and L depend on the actual situation.

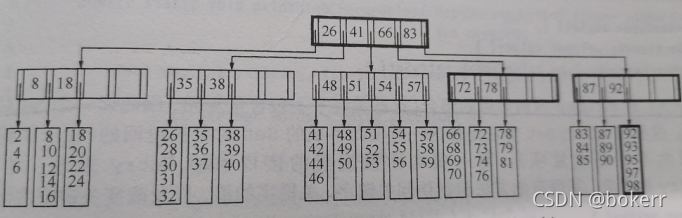
#Hahaha, drawing pictures is too troublesome. I took photos from the book Data Structure and Algorithm Analysis, and they are as witty as me.

Here we only talk about the definition of B-tree and the details of parameter selection. The insertion of B-tree and the deletion of B-tree are not discussed in detail.

4. B-tree index

Generally, the height of B-tree is 2~4 levels, that is, when searching for row records, it usually only takes 2~4 disk IO times to find the location where the row record is located. Page. Regardless of clustered index or non-clustered index, the interior is highly balanced, and the index data is stored in leaf nodes. The difference is that the leaf nodes of the clustered index store the entire row record data.

1. Clustered index

The leaf nodes of the clustered index store the entire row of data, and each table can only have one clustered index.

2. Auxiliary index

The leaf node of the auxiliary index stores the key value and a bookmark, which tells the Innodb storage engine where to find the complete data of the corresponding row record in the index.

Each table can have multiple auxiliary indexes

One disadvantage of the auxiliary index is that it must be discrete The clustered index gets the complete row data, even if the bookmark stored in the secondary index has been found.

5. About Cardinality value

The discussion of Cardinality is based on non-clustered index, and each non-clustered index will have a Cardinality value.

1. Cardinality definition

It should be noted that not all columns in the query conditions need to be indexed; for example, dictionaries with small value ranges and dense distribution such as gender, age, subjects, etc. No indexing is required.
Cardinality represents the estimated number of unique records in the index. Generally: Cardinality / number of record rows in the table should be as close to 1 as possible; if it is very small, you need to consider whether the index should be removed. (This value must be close to 1 in a clustered index, and there is no discussion value).

2. Update of Cardinality

• In MySQL, since each storage engine implements B-tree indexes differently, Cardinality statistics are implemented at the storage engine layer. .

• When the amount of data in the table is very large, it is very time-consuming to perform statistics on Cardinality, and its statistics are generally performed using the sampling method.

• The existence of Cardinality can help us analyze whether the index has any meaning.

6. Use of B-tree index

[The indexes discussed in this section mostly refer to auxiliary indexes, and queries on clustered indexes are generally called full table scans. 】

1. Joint index

The joint index is an index built on multiple columns on the table. It is also a B-tree structure. The only difference from a single index is that it has multiple columns.

create table t (
	a int,
	b int,
	primary key (a),
	key idx_ab (a, b)
)engine=innodb;

In the above table, set the joint primary key idx_ab, and its storage structure is as follows:

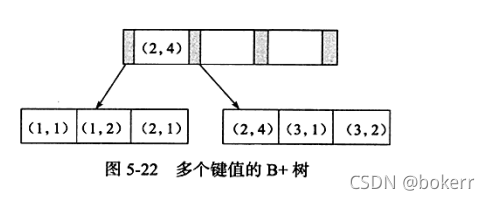
如上图所述，键值有序，需要注意的是，如下SQL可以使用该索引：

	select * from t where a = ? and b = ?
	
	select * from t where a = ?

如下sql 不能使用该索引；查看示例图中联合索引叶子节点存放的数据我们可以发现：两个叶子节点上，关于字段b的存放显然不是有序的。

	select * from t where b = ?

联合索引本身还有一个好处，辅助索引本身已经对第二个键值进行了排序，如下语句可以避免多一次的排序。

	select b from t where a = ?  order by b desc

辅助索引中已经对 b 列进行了排序，所以此时使用辅助索引更高效。

2、覆盖索引

Innodb 支持覆盖索引(covering index，或称为索引覆盖)，即从辅助索引中就可以得到结果，而不需要查询聚集索引中的记录。由于辅助索引不包含完整的行记录，从而比聚集索引小很多，可以极大地减少IO操作。

再形如：select count(*) from table name where b = ? 的sql，如果有满足条件的辅助索引，它会优先使用辅助索引因为辅助索引体积远远小于聚集索引。

3、优化器选择不使用索引的情况

某些情况下，通过EXPLAIN指令会发现一些SQL，并没有选择使用满足条件的辅助索引去查数据，而是直接选择了全表扫描(聚集索引)，这种情况一般发生于 范围查找、join链接操作等情况下。

当发生此类查找时，一般是查找一个较大范围内的数据，当范围较大时同样意味着大量的数据需要再进行一次书签访问去获取完整数据，已知顺序读取速度大于离散读取速度，所以此时不会使用辅助索引，而是直接查聚集索引(整表扫描)。一般情况下，当访问数据超过表中数据总数的20%时，索引覆盖不再适用，而需要进行全表扫描。）

	create table t (
		a int,
		b int,
		primary key (a,b),
		key idx_a (a)
	)engine=innodb;

如上定义表，a和b两列构成联合索引，列a上有独立的辅助索引，对于语句：

select * from  t where  a >= 3  and a<= 1000000;

按理说，该语句是可以选择使用辅助索引 idx_a 进行查找的，但是通过执行 explain 发现该语句发生了全表扫描(聚集索引)，而不是使用辅助索引： idx_a。

4、索引提示

索引提示指MySQL支持在SQL中显式的告诉优化器使用哪个索引。

当优化器选择索引错误，可以手动指定索引。[极小概率事件]

当索引太多时，优化器选择索引的操作时间开销大，此时可以手动指定索引。

使用索引提示的前提是我们自己要对sql的执行非常了解，非常明确该操作能带来更好的效率。

5、Multi-Range Read 优化 (MRR)

MySQL5.6版本开始支持Multi-Range Read (MRR) 优化，它的目的是减少磁盘的离散读，将离散的访问优化为相对有序的访问，它使用于 range ref eq_ref 类型的查询。

1).MRR优化有如下好处：

• 它使得数据访问变得较为顺序，当根据辅助索引查询时，会将查询结果按照主键排序后，再去聚集索引进行书签查询。

• 减少缓冲池中页被替换的次数；

• 批量处理对键值的查询操作；

2).对于 JOIN 和 范围查询，Innodb 中MRR的工作方式为：

• 将通过辅助索引查询到的数据放到一个缓存中，此时这些数据是按照辅助索引键值排序的；

• 将缓存中的数据按照主键顺序排序；

• 根据主键顺序访问实际数据文件；

想象一下，在缓冲池不够大的情况下进行大范围数据查询，会导致数据页频繁被从LRU列表中移除。如果被查询的辅助索引不是按主键排序的，可能会多次发生如下的情况：一个页在同一次查询中被剔出LRU列表后又再次被加载出来。

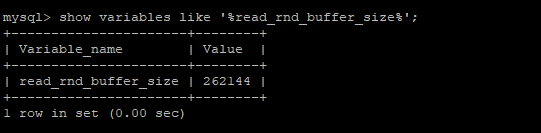
配置项：read_rnd_buffer_size 用来配置上述描述的键值缓冲区大小，默认为256K；当发生溢出时，执行器只对已经缓存的数据进行排序。

3).对于范围查询：MMR还支持对键值的拆分，将范围查询拆分为键值对进行批量的数据查询.

create table t (
	a integer,
	b integer,
	primary key (a),
	key idx_ab (a, b)
)engine=innodb;

select * from t where a = 50  and  b>= 100 and  b<= 20000

由于存在辅助索引 idx_ab，上述sql语句的条件可以拆分为键值对集合：{( 50 , 100 ),( 50 , 101 ),......,( 50 , 20000 )}，这样就将范围查询优化为对键值对的查询；否则会进行范围查询，将 b ∈ {100，20000} 的所有数据都取出。

Multi-Range Read 是否启用，由如下参数中的，mrr 和 mrr_cost_based 标记进行控制，mrr标记是 MRR优化的开关。若前者设置为on，后者设置为off表示当满足条件时总是使用MRR优化；若前者设置为 on，后者也设置 on 表示通过 cost base 方式判断是否需要 MRR优化。

6. Index Condition Pushdown Optimization (ICP)

ICP optimization is also supported starting from MySQL 5.6. It is an optimization method for querying based on the index. It supports Optimize queries of type: range, ref, eq_ref, ref_or_null.

• When ICP is disabled, the storage engine layer will traverse the index to locate the complete row record; then return it to the database layer (Server layer), and then perform where conditions for these data rows filter.

• When ICP is enabled, if the where condition can use the index, MySQL will put this part of the filtering operation into the storage engine layer. The storage engine filters through the index and takes out the entire data that satisfies the where condition. Row data and return. Using ICP can reduce the frequency with which the storage engine layer accesses row records, and at the same time reduces the number of times the database layer (Server layer) must access the storage engine.

[The prerequisite for using this filter is: the filter condition needs to be the range that the index can cover]

Index Condition Pushdown working principle As follows:

1) When ICP is not used

(1) When the storage engine reads the next row, it reads the relevant row record from the leaf node of the auxiliary index, and then uses the The primary key reference in the bookmark is returned to the database layer (Server layer) in order to query the complete row record.

(2) The database layer performs where condition filtering on the complete row records. If the row data meets the where condition, it will be used, otherwise it will be discarded.

(3) Perform step 1 until all data that meets the conditions are read.

2) How to perform an index scan when using ICP

(1) The storage engine reads data one by one from the index...

(2) Storage When the engine reads data from the index, it uses the where condition to filter based on the key of the index. If the row record does not meet the condition, the storage engine will process the next piece of data (return to the previous step). Only when the query conditions are met, the complete data will be read from the clustered index.

(3) Finally, the storage engine layer will return all complete row records that meet the query conditions to the database layer.

(4) If the database layer continues to be used, the query conditions after where that are not covered by the index will be filtered.

The above is the detailed content of Example analysis of indexes and algorithms of Mysql Innodb storage engine. For more information, please follow other related articles on the PHP Chinese website!