Don't blindly chase big models and pile up computing power! Shen Xiangyang, Cao Ying and Ma Yi proposed two basic principles for understanding AI: parsimony and self-consistency

In the past two years, large models that “make great efforts (computing power) can produce miracles” have become the trend pursued by most researchers in the field of artificial intelligence. However, the huge computational cost and resource consumption problems behind it have gradually become apparent. Some scientists have begun to take a serious look at large models and actively seek solutions. New research shows that achieving excellent performance of AI models does not necessarily rely on heap computing power and heap size.

Deep learning has been booming for ten years. It must be said that its opportunities and bottlenecks have attracted a lot of attention and discussion during these ten years of research and practice.

Among them, the bottleneck dimension, the most eye-catching is the black box characteristics of deep learning (lack of interpretability) and "miraculous results with great effort" (the model parameters are getting larger and larger, The demand for computing power is getting bigger and bigger, and the cost of computing is getting higher and higher). In addition, there are problems such as insufficient model stability and security vulnerabilities.

In essence, these problems are partly caused by the "open-loop" system nature of deep neural networks. To break the "curse" of the B-side of deep learning, it may not be enough to simply expand the model scale and computing power. Instead, we need to trace the source, from the basic principles of artificial intelligence systems, and from a new perspective (such as closed loop) Understand "intelligence".

On July 12, three well-known Chinese scientists in the field of artificial intelligence, Ma Yi, Cao Ying and Shun Xiangyang, jointly published an article on arXiv, "On the Principles of Parsimony and Self-Consistency for the Emergence of Intelligence", which proposes a new framework for understanding deep networks: compressive closed-loop transcription.

This framework contains two principles: parsimony and self-consistency, which respectively correspond to "what to learn" in the AI ​​model learning process. and "how to learn" are considered to be the two foundations of artificial/natural intelligence, and have attracted widespread attention in the field of artificial intelligence research at home and abroad.

Paper link:

https://arxiv.org/pdf/2207.04630.pdf

Three scientists believe that real intelligence must have two characteristics, one is interpretability, and the other is computability.

However, over the past decade, advances in artificial intelligence have been primarily based on deep learning methods that use “brute force” training of models, in which case although the AI ​​model can also gain functionality Modules are used for perception and decision-making, but the learned feature representations are often implicit and difficult to interpret.

In addition, relying solely on computing power to train models has also caused the scale of AI models to continue to increase, and the computing costs have continued to increase, and many problems have arisen in landing applications, such as neural networks. Collapse leads to a lack of diversity in learned representations, pattern collapse leads to a lack of stability in training, models have poor sensitivity to adaptability and catastrophic forgetting, and so on.

Three scientists believe that the above problem occurs because in the current deep network, the training of the discriminative model for classification and the generative model for sampling or replay are Mostly separate. Such models are typically open-loop systems that require end-to-end training through supervision or self-supervision. Wiener and others have long discovered that such an open-loop system cannot automatically correct errors in predictions, nor can it adapt to changes in the environment.

Therefore, they advocate the introduction of "closed-loop feedback" into the control system so that the system can learn to correct errors on its own. In this study, they also found that by using the discriminative model and the generative model to form a complete closed-loop system, the system can learn independently (without external supervision), and is more efficient, stable, and adaptable.

Note: From left to right are Shun Xiangyang (President's Professor of Hong Kong, China and Shenzhen, foreign academician of the National Academy of Engineering, former global executive vice president of Microsoft) , Cao Ying (Academician of the National Academy of Sciences, Professor at the University of California, Berkeley) and Ma Yi (Professor at the University of California, Berkeley).

Two principles of intelligence: parsimony and self-consistency

In this work, three scientists propose an explanation The two basic principles of artificial intelligence are parsimony and self-consistency (also known as "self-consistency"). Taking visual image data modeling as an example, it is deduced from the first principles of parsimony and self-consistency A compressed closed-loop transcription framework is proposed.

SIMPLICITY

The so-called simplicity is "what to learn". The principle of intelligent parsimony requires systems to obtain compact and structured representations in a computationally efficient manner. That is, intelligent systems can use any structured model that describes the world, as long as they can simply and efficiently simulate useful structures in real-life sensory data. The system should be able to accurately and efficiently assess the quality of a learning model using metrics that are fundamental, universal, easy to compute and optimize.

Taking visual data modeling as an example, the parsimony principle tries to find a (nonlinear) transformation f to achieve the following goals:

Compression: High-dimensional sensory data x Map to a low-dimensional representation z;

Linearization: map each type of object distributed on the nonlinear submanifold to a linear subspace;

Scarification: convert different The classes map to subspaces with independent or maximally incoherent basis.

That is, real-world data that may be located on a series of low-dimensional submanifolds in a high-dimensional space are converted into independent low-dimensional linear subspace series. This model is called "linear discriminative representation" (LDR). The compression process is shown in Figure 2:

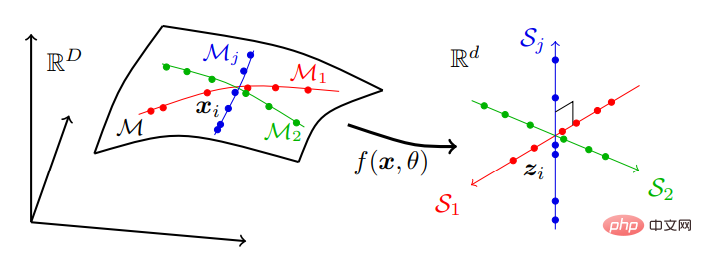
Figure 2: Seeking linear sum discriminative representation, Mapping high-dimensional sensory data, typically distributed over many nonlinear low-dimensional submanifolds, to a set of independent linear subspaces with the same dimensions as the submanifolds.

In the family of LDR models, there is an intrinsic measure of parsimony. That is, given an LDR, we can calculate the total "volume" spanned by all features over all subspaces and the sum of the "volume" spanned by features of each category. The ratio between these two volumes then gives a natural measure of how good the LDR model is (bigger is often better).

According to information theory, the volume of a distribution can be measured by its rate distortion.

A work "ReduNet: A White-box Deep Network from the Principle of Maximizing Rate Reduction" by Ma Yi's team in 2022 shows that if you use a Gaussian rate distortion function and choose a A general-purpose deep network (such as ResNet) models the mapping f(x, θ) by minimizing the encoding rate.

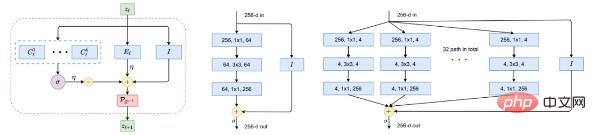
# Figure 5: Building blocks of nonlinear mapping f. Left: A layer of ReduNet, as an iteration of projected gradient ascent, consisting precisely of expanding or compressing linear operators, nonlinear softmax, skip connections and normalization. Middle and right of the figure: one layer of ResNet and ResNeXt respectively.

Astute readers may have recognized that such a diagram is very similar to popular "tried and true" deep networks such as ResNet (Figure 5, middle), including parallel columns in ResNeXt (Figure 5 right) and Mix of Experts (MoE).

From the perspective of unfolding the optimization scheme, this provides a powerful explanation for a class of deep neural networks. Even before the rise of modern deep networks, iterative optimization schemes for seeking sparsity such as ISTA or FISTA were interpreted as learnable deep networks.

Through experiments, they demonstrate that compression can give birth to a constructive way to derive deep neural networks, including their architecture and parameters, as a fully interpretable white box: Its layers perform iterative and incremental optimizations toward the principled goal of promoting simplicity. Therefore, for the deep networks thus obtained, ReduNets, starting from data X as input, the operators and parameters of each layer are constructed and initialized in a fully forward-unfolded manner.

This is very different from popular practice in deep learning: starting with a randomly constructed and initialized network and then making global adjustments through backpropagation. It is generally believed that the brain is unlikely to utilize backpropagation as its learning mechanism due to the need for symmetrical synapses and complex forms of feedback. Here, the forward unroll optimization relies only on operations between adjacent layers that can be hardwired and therefore easier to implement and exploit.

The "evolution" of artificial neural networks over the past decade is easy to understand and particularly helpful once we realize that the role of deep networks themselves is to perform (gradient-based) iterative optimization to compress, linearize and sparsify data. Yu explains why only a few AI systems stand out through a human selection process: from MLP to CNN to ResNet to Transformer.

In contrast, random searches for network structures, such as neural architecture search, do not produce network architectures that can effectively perform common tasks. They hypothesize that successful architectures become increasingly effective and flexible in simulating iterative optimization schemes for data compression. This can be exemplified by the previously mentioned similarities between ReduNet and ResNet/ResNeXt. Of course, there are many other examples.

Self-consistency

Self-consistency is about "how to learn", that is, autonomous intelligent systems learn by minimizing the observed and the reproducer to find the most self-consistent model to observe the external world.

The principle of parsimony alone does not ensure that the learning model can capture all the important information in perceiving the external world data.

For example, mapping each class to a one-dimensional "one-hot" vector by minimizing cross-entropy can be viewed as a parsimonious form. It may learn a good classifier, but the learned features collapse into singletons, known as "nervous collapse." The features thus learned do not contain enough information to regenerate the original data. Even if we consider the more general class of LDR models, the speed reduction objective alone does not automatically determine the correct dimensions of the environment feature space. If the feature space dimension is too low, the learned model will underfit the data; if it is too high, the model may overfit.

In their view, the goal of perception is to learn all predictable perceptual content. An intelligent system should be able to regenerate a distribution of observed data from a compressed representation that, once generated, it itself cannot distinguish, no matter how hard it tries.

The paper emphasizes that the two principles of self-consistency and parsimony are highly complementary and should always be used together. Self-consistency alone does not ensure gains in compression or efficiency.

Mathematically and computationally, fit any training data using an over-parameterized model or ensure consistency by establishing a one-to-one mapping between domains with the same dimensions, while It is easy without learning the intrinsic structure in the data distribution. Only through compression can intelligent systems be forced to discover intrinsic low-dimensional structures in high-dimensional sensory data and transform and represent these structures in the feature space in the most compact way for future use.

Furthermore, only through compression can we easily understand the reasons for over-parameterization. For example, like DNN, which usually performs feature boosting through hundreds of channels, if its pure purpose is to Compression in dimensional feature space does not lead to overfitting: boosting helps reduce nonlinearities in the data, making it easier to compress and linearize. The role of subsequent layers is to perform compression (and linearization), and generally the more layers, the better the compression.

In the special case of compressing to a structured representation such as LDR, the paper refers to a type of automatic encoding (see the original paper for details) as "transcription". The difficulty here is making the goal computationally tractable and thus physically achievable.

The rate reduction ΔR gives an unambiguous primary distance measure between degenerate distributions. But it only works for subspaces or mixtures of Gaussians, not for general distributions! And we can only expect the distribution of the internal structured representation z to be a mixture of subspaces or Gaussians, not the original data x.

This leads to a rather profound question about learning "self-consistent" representations: in order to verify that an internal model of the external world is correct, an autonomous system really needs to measure differences in the data space ?

the answer is negative.

The key is to realize that to compare x and x^, the agent only needs to compare their respective internal features z = f(x) and z^ = via the same mapping f f(x^), to make z compact and structured.

Measuring distribution differences in z space is actually well-defined and valid: it can be said that in natural intelligence, there are independent autonomous systems for learning internal measurement differences The only thing the brain can do.

This effectively generates a "closed loop" feedback system, with the entire process shown in Figure 6.

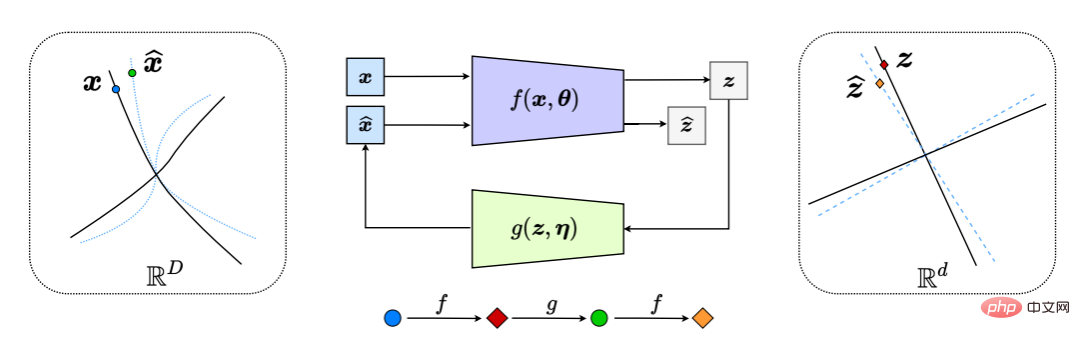
Figure 6: Compressed closed-loop transcription of nonlinear data submanifolds to LDR (by internally comparing and minimizing the difference between z and z^). This results in a natural chase-and-flight game between the encoder/sensor f and the decoder/controller g, such that the distribution of the decoded x^ (blue dashed line) chases and matches the distribution of the observed data x (black solid line) .

One can interpret the popular practice of learning a DNN classifier f or generator g separately as learning the open-ended part of a closed-loop system (Figure 6). This currently popular approach is very similar to open-loop control, which the control field has long known to be problematic and expensive: training such a part requires supervision of the desired output (such as a class label); if the data distribution, system parameters, or tasks occur changes, the deployment of such open-loop systems inherently lacks stability, robustness, or adaptability. For example, deep classification networks trained in a supervised environment often suffer catastrophic forgetting if retrained to handle new tasks with new data categories.

In contrast, closed-loop systems are inherently more stable and adaptive. In fact, Hinton et al. already proposed this in 1995. The discriminative and generative parts need to be combined as the "wake" and "sleep" phases of the complete learning process, respectively.

However, simply closing the loop is not enough.

The paper advocates that any intelligent agent needs an internal game mechanism to be able to self-learn through self-criticism! What follows here is the concept of gaming as a universally effective way of learning: repeatedly applying a current model or strategy against adversarial criticism, thereby continuously improving the model or strategy based on the feedback received through a closed loop!

Within such a framework, the encoder f plays a dual role: in addition to learning a representation z of the data x by maximizing the rate reduction ΔR(Z) (as done in Section 2.1 that), it should also act as a feedback "sensor", actively detecting the difference between the data x and the generated x^. The decoder g also plays a dual role: it is a controller, linked to the difference between x and xˆ detected by f; it is also a decoder, trying to minimize the overall coding rate to achieve the goal (giving way certain accuracy).

Therefore, the optimal "parsimonious" and "self-consistent" representation tuple (z, f, g) can be interpreted as between f(θ) and g(η) The equilibrium point of a zero-sum game, rather than the utility based on the combination rate reduction:

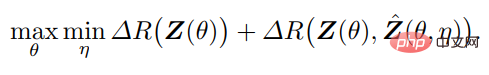
The above discussion is the performance of the two principles in a supervised situation .

But the paper emphasizes that the compressed closed-loop transcription framework they proposed is capable of self-learning through self-monitoring and self-criticism!

Additionally, since the rate reduction has found an explicit (subspace type) representation for the learning structure, making past knowledge easier to retain when learning new tasks/data, it can be used as a self-preserving Consistent priors (memory).

Recent empirical work shows that this can yield the first self-contained neural system with fixed memory that can incrementally learn good LDR representations without suffering catastrophic forgetting. For such a closed-loop system, forgetting (if anything) is quite elegant.

Additionally, the learned representation can be further consolidated when images of old categories are fed to the system again for review—a feature that is very similar to that of human memory. In a sense, this constrained closed-loop formulation essentially ensures that visual memory formation can be Bayesian and adaptive—assuming these characteristics are ideal for the brain.

As shown in Figure 8, the automatic encoding learned in this way not only shows good sample consistency, but the learned features also show clear and meaningful local low-dimensional (thin )structure.

Figure 8: Left: Auto-encoded x vs. Comparison between decoded x^. Right: t-SNE of unsupervised learned features for 10 classes, and visualization of several neighborhoods and their associated images. Note the locally thin (nearly one-dimensional) structure in the visualized features, projected from a feature space of hundreds of dimensions.

What is even more surprising is that even when no class information is provided during training, subspace or feature-related block diagonal structures start to appear in the features learned for the class ( Figure 9)! Therefore, the structure of the learned features is similar to the category-selective regions observed in the primate brain.

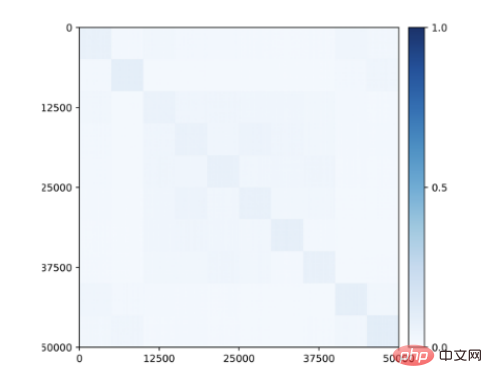
Figure 9: Correlations between unsupervised learned features for 50,000 images belonging to 10 categories (CIFAR-10) via closed-loop transcription. Class-consistent block diagonal structures emerge without any supervision.

Universal Learning Engine: Combining 3D Vision and Graphics

Summary of the paper, simplicity and self-consistency reveal that the role of deep networks is to become a combination of external observation and internal representation. nonlinear mapping model.

In addition, the paper emphasizes that closed-loop compression structures are ubiquitous in nature and are applicable to all intelligent creatures. This can be seen in the brain (compression of sensory information), spinal cord circuits (compression of muscle movement) ), DNA (compressed functional information of proteins), and other biological examples. Therefore, they believe that compressed closed-loop transcription may be the universal learning engine behind all intelligent behavior. It enables intelligent organisms and systems to discover and refine low-dimensional structures from seemingly complex and unorganized inputs, and convert them into compact and organized internal structures that can be remembered and utilized.

To illustrate the generality of this framework, the paper examines two other tasks: 3D perception and decision-making (which LeCun considers two key modules of autonomous intelligent systems). This article is organized and only introduces the closed loop of computer vision and computer graphics in 3D perception.

The classic paradigm of 3D vision proposed by David Marr in his influential book Vision advocates a "divide and conquer" approach, dividing the 3D perception task into several modular Process: From low-level 2D processing (e.g., edge detection, contour sketching), to mid-level 2.5D parsing (e.g., grouping, segmentation, shape, and ground), to high-level 3D reconstruction (e.g., pose, shape) and recognition (e.g., object), and conversely, The compressed closed-loop transcription framework promotes the idea of ​​"joint construction".

Perception is compressed closed-loop transcription? More precisely, 3D representations of the shape, appearance, and even dynamics of objects in the world should be the most compact and structured representations developed internally by our brains to interpret all perceived visual observations accordingly. If so, then these two principles suggest that a compact and structured 3D representation is the internal model to look for. This means that we can and should unify computer vision and computer graphics within a closed-loop computing framework, as shown in the following figure:

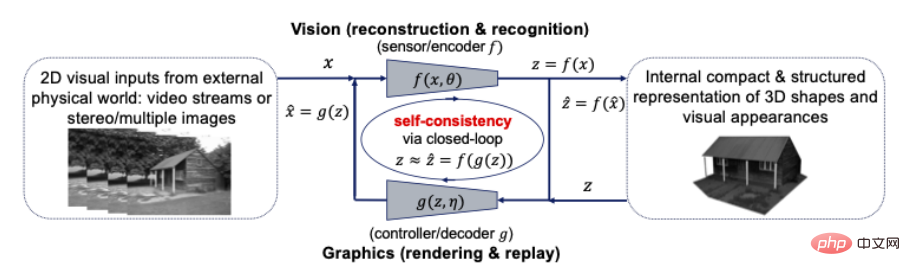
Figure 10: The connection between computer vision and graphics Closed-loop, compact and structured 3D models for visual input

Computer vision is often explained as the forward process of reconstructing and identifying internal 3D models for all 2D visual input, while computer graphics represents its inverse process of rendering and animating internal 3D models. Combining these two processes directly into a closed-loop system may bring huge computational and practical benefits: all the rich structures in geometry, visual appearance and dynamics (such as sparsity and smoothness) can be used together in a unified 3D model, the most compact and consistent with all visual inputs.

Recognition techniques in computer vision can help computer graphics build compact models in shape and appearance space and provide new ways to create realistic 3D content. On the other hand, 3D modeling and simulation techniques in computer graphics can predict, learn, and verify the properties and behavior of real objects and scenes analyzed by computer vision algorithms. The visual and graphics community has long practiced a "synthetic analysis" approach.

Uniform representation of appearance and shape? Image-based rendering, where new views are generated by learning from a given set of images, can be seen as an early attempt to bridge the gap between vision and graphics with parsimonious and self-consistent principles. In particular, plenoptic sampling shows that anti-aliased images (self-consistency) can be achieved with the minimum number of images required (parsimony).

Broader Intelligence

The Neuroscience of Intelligence

One would expect basic intelligence principles to inform the design of the brain Significant impact. The principles of parsimony and self-consistency shed new light on several experimental observations of the primate visual system. More importantly, they reveal what to look for in future experiments.

The author team has demonstrated that simply seeking internal parsimonious and predictive representations is sufficient to achieve "self-supervision," allowing structure to automatically appear in the final representation learned through compressed closed-loop transcription.

For example, Figure 9 shows that unsupervised data transcription learning automatically distinguishes features of different categories, providing an explanation for the category-selective representations observed in the brain. These features also provide a reasonable explanation for the widespread observations of sparse coding and subspace coding in primate brains. Furthermore, in addition to visual data modeling, recent neuroscience research suggests that other structured representations arising in the brain (such as “place cells”) may also be the result of encoding spatial information in the most compressed manner.

It can be said that the maximum coding rate reduction (MCR2) principle is similar in spirit to the "free energy minimization principle" in cognitive science, which attempts to Provides a framework for Bayesian inference through energy minimization. But unlike the general concept of free energy, rate reduction is computationally tractable and directly optimizable because it can be expressed in a closed form. Furthermore, the interaction of these two principles suggests that autonomous learning of the correct model (class) should be accomplished through a closed-loop maximization game of this utility, rather than minimization alone. Therefore, they believe that the compressed closed-loop transcription framework provides a new perspective on how Bayesian inference can be practically implemented.

This framework is also believed by them to illustrate the overall learning architecture used by the brain, which can build feed-forward segments by unfolding optimization schemes without the need to learn from random networks through backpropagation . In addition, there is a complementary generative part of the framework that can form a closed-loop feedback system to guide learning.

Finally, the framework reveals the elusive "prediction error" signal sought by many neuroscientists interested in the brain mechanisms of "predictive coding," a type of closed-loop transcription that is related to compression Computational scheme to generate resonance: To make the computation easier, the difference between the incoming and generated observations should be measured at the final stage of the representation.

Towards a higher level of intelligence

The work of Ma Yi et al. believes that compressed closed-loop transcription is the same as that proposed by Hinton et al. in 1995 Compared with other frameworks, it is computationally easier to process and scalable. Moreover, recurrent learning of nonlinear encoding/decoding mappings (often manifested as deep networks) essentially provides an important bridge between external unorganized raw sensory data (such as vision, hearing, etc.) and internal compact and structured representations. "interface".

However, they also pointed out that these two principles do not necessarily explain all aspects of intelligence. The computational mechanisms underlying the emergence and development of high-level semantic, symbolic, or logical reasoning remain elusive. To this day, there is debate over whether this advanced symbolic intelligence can arise from continuous learning or must be hard-coded.

In the view of the three scientists, structured internal representations such as subspaces are a necessary intermediate step for the emergence of high-level semantic or symbolic concepts - each subspace corresponds to a discrete ( object) category. Other statistical, causal or logical relationships between such abstract discrete concepts can be further simplified and modeled as compact and structured (e.g. sparse) graphs, with each node representing a subspace/category. Graphs can be learned through automatic encoding to ensure self-consistency.

They speculate that the emergence and development of advanced intelligence (with sharable symbolic knowledge) is only possible on top of compact and structured representations learned by individual agents. Therefore, they suggested that new principles for the emergence of advanced intelligence (if advanced intelligence exists) should be explored through effective information exchange or knowledge transfer between intelligent systems.

Furthermore, higher-level intelligence should have two things in common with the two principles we propose in this article:

• Interpretability: All The principles should all help to reveal intelligent computational mechanisms as white boxes, including measurable goals, associated computational architectures, and structures for learning representations.
• Computability: Any new intelligence principle must be computationally tractable and scalable, achievable through computers or natural physics, and ultimately substantiated by scientific evidence.

Only with interpretability and computability can we advance the progress of artificial intelligence without relying on the current expensive and time-consuming "trial and error" methods and be able to describe and complete these The minimum data and computing resources required for the task, rather than simply advocating a “bigger is better” brute force approach. Wisdom should not be the prerogative of the most resourceful people. With the right set of principles, anyone should be able to design and build the next generation of intelligent systems, large or small, whose autonomy, capabilities, and efficiency can ultimately mimic or even surpass those of animals and humans. Humanity.

Paper link:

​https://arxiv.org/pdf/2207.04630.pdf​

The above is the detailed content of Don't blindly chase big models and pile up computing power! Shen Xiangyang, Cao Ying and Ma Yi proposed two basic principles for understanding AI: parsimony and self-consistency. For more information, please follow other related articles on the PHP Chinese website!