Home >Technology peripherals >AI >What is the relationship between quantum computing and artificial intelligence?
What is the relationship between quantum computing and artificial intelligence?
- WBOYforward
- 2023-05-05 08:37:061301browse

After decades of research, artificial intelligence (AI) is becoming one of the major industry trends. From conversations with Alexa and Siri, to Waymo and Tesla’s self-driving cars, OpenAI’s GPT-3 writing prose like a human, and DeepMind’s AlphaZero beating a human Go grandmaster, artificial intelligence is now Mature enough. Solve real-life problems, often faster and better than humans.
Elsewhere in the tech industry, some visionaries are working to develop quantum computers, which seek to exploit the properties of quantum physics to perform calculations faster than today's computers.
At this point, many people may be wondering: What exactly is the relationship between quantum computing and artificial intelligence?
Algorithmic complexity is the hidden enemy
Algorithmic complexity is A somewhat obscure mathematical concept that ties together the work done by AI researchers and quantum computing pioneers.
Computational complexity theory is a field spanning mathematics and computer science that focuses on classifying computational problems based on resource usage, such as space (memory) and time. Essentially, a computational problem is a task that can be solved mechanically by a computer, following mathematical steps defined in an algorithm.
For example, consider the problem of sorting numbers in a list. One possible algorithm, called "selection sort", consists of repeatedly finding the smallest element (in ascending order) from the unsorted part of the list (initially all) and placing it at the beginning. The algorithm effectively maintains two sublists of the original list as it runs: the already sorted part and the remaining unsorted part. After this process goes through several times, the result is a sorted list from smallest to largest. In terms of time complexity, this is represented by a complexity of N 2, where N represents the size or number of elements in the list. Mathematicians have proposed more efficient but more complex sorting algorithms such as "Cube Sort" or "Tim Sort", both of which have a complexity of N x log(N). Sorting a list of 100 elements is a simple task for today's computers, but sorting a list of a billion records may not be as simple. Therefore, time complexity (or the number of steps in an algorithm relative to the size of the input problem) is very important.
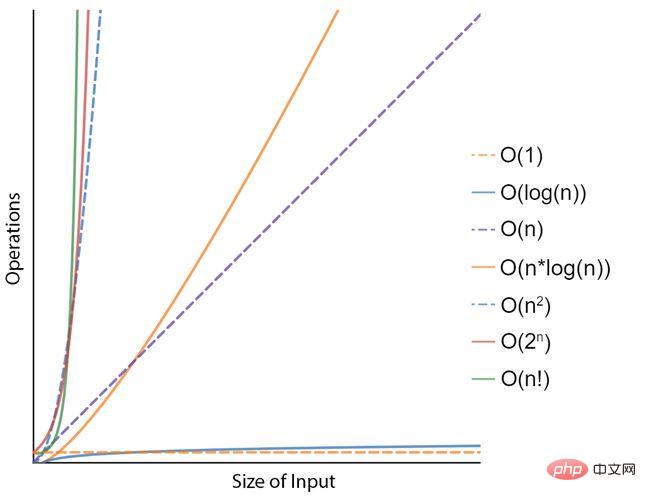
#To solve a problem faster, you can use a faster computer, or find a more efficient algorithm that requires fewer operations, which is what lower time complexity means. However, it's clear that for problems of exponential complexity (e.g. N 2 or 2 N) the math works against you, and for larger problem sizes just using a faster computer isn't practical. And this is precisely the case in the field of artificial intelligence.
Artificial intelligence is a highly complex problem to solve
First, we will look at the computational complexity of the artificial neural networks used in today's artificial intelligence (AI) systems. These mathematical models are inspired by the biological neural networks that make up animal brains. They "learn" to recognize or classify input data by seeing many examples. They are collections of interconnected nodes or neurons, combined with an activation function that determines the output based on the data presented in an "input layer" and the weights in the interconnections.
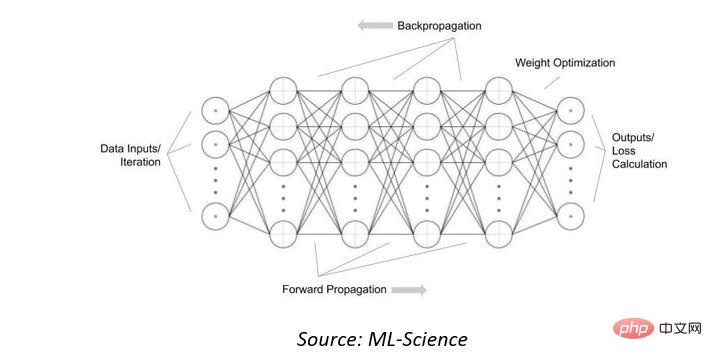
In order to adjust the weights in the interconnections so that the "output" is useful or correct, it can be "trained" by exposing it to many data examples and "backpropagating" the output loss network.
For a neural network with N inputs and M hidden layers, where the i-th hidden layer contains m i hidden neurons and k output neurons, the algorithm for adjusting the weights of all neurons (called the inverse propagation algorithm) will have a time complexity of: Prose, with 175 billion parameters (or neurons). With billions of M, this AI model currently takes months to train, even using powerful server computers in large cloud data centers. Additionally, AI models will continue to grow in size, so things will get worse over time.
Quantum computing comes to the rescue?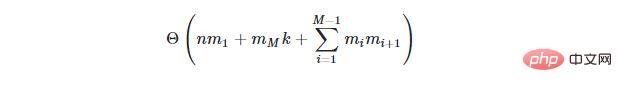
Classical computers transmit information in bits (short for "binary digits"), while quantum computers use qubits (short for "qubits"). Like classical bits, qubits must ultimately transmit information in the form of either a 1 or a 0, but what's special is that they can represent both a 1 and a 0 at the same time. A qubit is said to have a probability distribution such that it has a 70% chance of being a 1 and a 30% chance of being a 0. This is what makes quantum computers so special.
Quantum computers take advantage of two fundamental properties in quantum mechanics: superposition and entanglement.
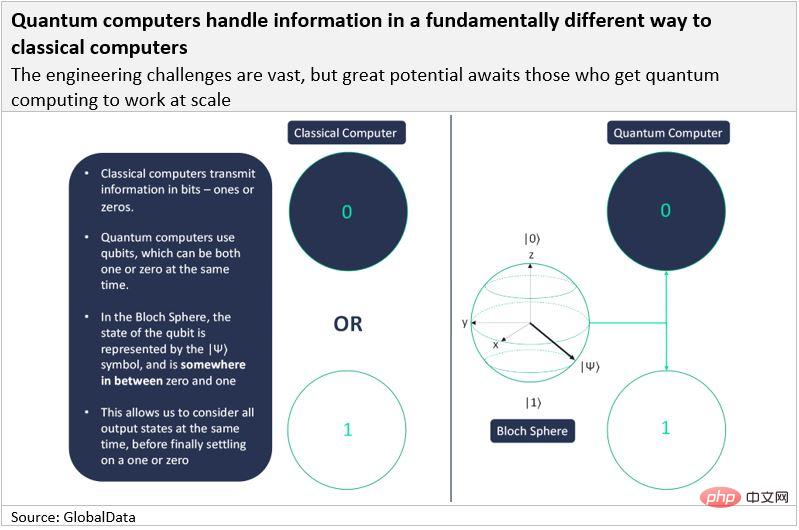
When a qubit is 1 and 0 at the same time, it is said to be in a superposition state. Superposition is a general term for conditions when a system is in multiple states simultaneously and only a single state is assumed at the time of measurement. If we assume that a coin is a quantum object, then when the coin is flipped, a superposition results: the coin only has a probability of heads or tails. Once the coin hits the ground and we measure it, we know whether the coin is heads or tails. Likewise, only when we measure the electron's spin (similar to a coin falling to the ground) do we know what state the electron is in and whether it is a 1 or a 0.
Superposition of quantum particles is only useful when we have multiple particles. This brings us to the second fundamental principle of quantum mechanics: entanglement. Two (or more) entangled particles cannot be described individually; their properties are entirely dependent on each other. Thus, entangled qubits can influence each other. The probability distribution of one qubit (one or zero) depends on the probability distribution of all other qubits in the system.
Because of this, each new qubit added to the system doubles the number of states the computer can analyze. This exponential increase in computer power contrasts with classical computing, which scales only linearly with each new bit.
Theoretically, entangled qubits can perform billions of operations simultaneously. It is clear that this capability will provide significant acceleration for any algorithm with complexity in the range of N2, 2N, or N.
Getting Ready for Quantum-Powered Artificial Intelligence
Due to the vast potential of quantum computing, while hardware teams continue to work on making these systems a reality (the largest to date is IBM’s 127-Qubit Eagle system), but software researchers are already working on new algorithms that can take advantage of this "simultaneous computing" capability, in fields such as cryptography, chemistry, materials science, system optimization, and machine learning/artificial intelligence. It is believed that Shor's factored quantum algorithm will provide exponential speedups over classical computers, which poses a risk to current cryptographic algorithms.
Most interestingly, it is believed that quantum linear algebra will provide polynomial acceleration, which will greatly improve the performance of our artificial neural networks. Google has launched TensorFlow Quantum, a software framework for quantum machine learning that allows rapid prototyping of hybrid quantum-classical machine learning models. Also a leader in quantum computing, IBM recently announced that it had discovered "mathematical proof" of quantum superiority for quantum machine learning. However, while companies like IBM and Google are vertically integrated (and thus develop hardware systems and software algorithms simultaneously) , but there is also a group of very interesting quantum software startups, including Zapata, Riverlane, 1Qbit, and, to an extent, Quantinuum (which is no longer a pure software company since Cambridge Quantum Computing merged with Honeywell and changed its name), just To give a few examples.
As quantum hardware becomes more powerful and quantum machine learning algorithms are refined, quantum computing is likely to capture a significant share of the artificial intelligence chip market.
The above is the detailed content of What is the relationship between quantum computing and artificial intelligence?. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- Technology trends to watch in 2023
- How Artificial Intelligence is Bringing New Everyday Work to Data Center Teams
- Can artificial intelligence or automation solve the problem of low energy efficiency in buildings?
- OpenAI co-founder interviewed by Huang Renxun: GPT-4's reasoning capabilities have not yet reached expectations
- Microsoft's Bing surpasses Google in search traffic thanks to OpenAI technology

