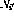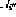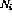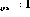Home >Technology peripherals >AI >Turing machine is the hottest recurrent neural network RNN in deep learning? The 1996 paper proved it!
Turing machine is the hottest recurrent neural network RNN in deep learning? The 1996 paper proved it!
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBforward
- 2023-04-25 21:25:06837browse
The Finnish Artificial Intelligence Conference organized by the Finnish Artificial Intelligence Association and the University of Vaasa was held in Vaasa, Finland from August 19 to 23, 1996.
A paper published at the conference proved that the Turing machine is a recurrent neural network.
Yes, this was 26 years ago!
Let us take a look at this paper published in 1996.
1 Preface
1.1 Neural Network Classification
Neural networks can be used for classification tasks to determine whether the input pattern belongs to a specific category.
It has long been known that single-layer feedforward networks can only be used to classify linearly separable patterns, that is, the more consecutive layers, the more complex the distribution of classes.
When feedback is introduced in the network structure, the perceptron output value is recycled, and the number of consecutive layers becomes infinite in principle.
Has the computing power been qualitatively improved? The answer is yes.
For example, you can construct a classifier to determine whether the input integer is prime.
It turns out that the size of the network used for this purpose can be finite, and even if the input integer size is not limited, the number of primes that can be correctly classified is infinite.
In this article, "a cyclic network structure composed of the same computational elements" can be used to complete any (algorithmically) computable function.
1.2 About computability
According to the basic axioms of computability theory, Turing machines can be used to implement computable functions. There are many ways to implement Turing machines.
Define programming language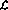 . The language has four basic operations:
. The language has four basic operations:

Here, V represents any variable with a positive integer value, j represents any line number.
It can be shown that if a function is Turing computable, it can be encoded using this simple language (see [1] for details) .
2 Turing Network
2.1 Recursive Neural Network Structure
The neural network studied in this article consists of perceptrons, all of which have the same The structure of the perceptron number q can be defined as
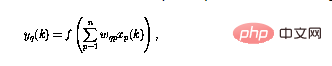
. Among them, the perceptron output at the current moment (using 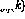 represents) is calculated using n input
represents) is calculated using n input  .
.
Nonlinear function f can now be defined as
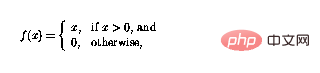
so that the function can Simply "cutting off" negative values, loops in a perceptron network means that perceptrons can be combined in complex ways.
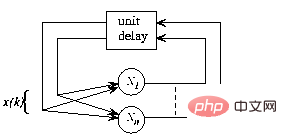
Figure 1 The overall framework of the recurrent neural network, the structure is autonomous without external input, and the network behavior is completely determined by the initial state
In Figure 1 , the recursive structure is shown in a general framework: now 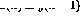 and n are the numbers of perceptrons, and the connection from perceptron p to perceptron q is given by
and n are the numbers of perceptrons, and the connection from perceptron p to perceptron q is given by 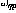 Scalar weight representation.
Scalar weight representation.
That is, given an initial state, the network state will iterate until it no longer changes, and the results can be read at the stable state or the "fixed point" of the network.
2.2 Neural Network Construction
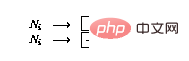
The following explains how the program is implemented in the perceptron network. The network consists of the following nodes (or perceptrons):
is implemented in the perceptron network. The network consists of the following nodes (or perceptrons):
-
For every variable V in the program, there is a variable node
 .
. -
For each program line i, there is an instruction node
 .
. -
For each conditional branch instruction on line i, there are two additional branch nodes
 and
and  .
.
Language The implementation of the program includes the following changes to the perceptron network:
The implementation of the program includes the following changes to the perceptron network:
- For the program For each variable in V, use the following link to expand the network:

-
If the program code If there is no operation () on line i
 , use the following link to expand the network (assuming the node
, use the following link to expand the network (assuming the node  exists:
exists:

-
If there is an incremental operation () in line i
 , expand the network as follows:
, expand the network as follows:

-
If there is a decrement operation () in line i
 , expand the network as follows:
, expand the network as follows:
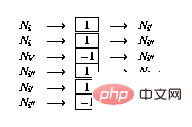
-
If there is a conditional branch () at line i
 , expand the network as follows:
, expand the network as follows:
2.3 Equivalence Proof
What needs to be proved now is that "the internal state of the network or the content of the network node" can be identified by the program state, while the network Continuity of state corresponds to program flow.
Define the "legal state" of the network as follows:
-
to all transition nodes
 and The output of
and The output of  (as defined in 2.2) is zero (
(as defined in 2.2) is zero ( );
);
-
at most one instruction node
 has a unit output (
has a unit output ( ), all other instruction nodes have a zero output, and the
), all other instruction nodes have a zero output, and the
- variable node has a non-negative integer output value.
If the outputs of all instruction nodes are zero, the state is the final state . A legal network state can be directly interpreted as a program "snapshot" - if , the program counter is at line i, and the corresponding variable value is stored in in the variable node.
Changes in network status are activated by non-zero nodes.
First, focusing on the variable nodes, it turns out that they behave like integrators and the previous contents of the node are looped back to the same node.
The only connections from variable nodes to other nodes have negative weights - that's why nodes containing zeros don't change, because of non-linearity (2).
Next, the instruction node is explained in detail. Assume that the only non-zero instruction node is at time k---this corresponds to the program counter at line i in the program code .
If line i in the program is , then the behavior of the network taking one step forward can be expressed as ( Only affected nodes shown)
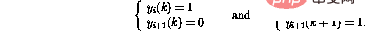
It turns out that the new network state is legitimate again. Compared to the program code, this corresponds to the program counter being moved to line i 1.
On the other hand, if line i in the program is 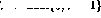 , then the behavior of one step forward is
, then the behavior of one step forward is
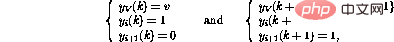
In this way, in addition to moving the program counter to the next line, the value of the variable V will also be decremented. If line i were
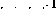 , the operation of the network would be the same except that the value of variable V is increased.
, the operation of the network would be the same except that the value of variable V is increased.
The conditional branch operation (IF GOTO 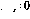 j) at line i activates a more complex sequence of operations :
j) at line i activates a more complex sequence of operations :
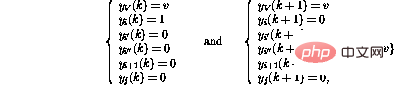
##Finally,
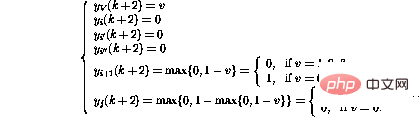
It turns out that in these After the step, the network state can again be interpreted as another program snapshot.
The variable value has been changed and the token has been moved to the new location as if the corresponding program line had been executed.
If the token disappears, the network state no longer changes - this can only happen if the program counter "exceeds" the program code, which means the program terminates.
The operation of the network is also similar to the operation of the corresponding program, and the proof is completed.
3 Modification3.1 Extension
It is easy to define additional streamlined instructions that can make programming easier, And the generated program is more readable and executes faster. For example, the unconditional branch (GOTO j) at line
- ## at line
- i can be implemented as
Add the constant c to the variable at line - i () can be implemented as ## Another conditional branch (IF V
=0 GOTO j) on line -
can be achieved For
Additionally, various increment/decrement instructions can be evaluated simultaneously. Suppose you want to perform the following operations: - . Only one node is needed :
The above method is by no means an implementation of a Turing machine the only way.
This is a simple implementation and may not necessarily be optimal in an application.
3.2 Matrix formulation
The above construction can also be implemented in the form of a matrix.
The basic idea is to store the variable value and "program counter" in the process state s, and let the state transition matrix
Arepresent the node links between. The operation of the matrix structure can be defined as a discrete-time dynamic process
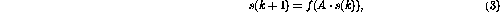
where the nonlinear vector-valued function  is now defined element-wise as in (2).
is now defined element-wise as in (2).
The contents of the state transition matrixA are easily decoded from the network formula - the matrix elements are the weights between nodes.
This matrix formula is similar to the "concept matrix" framework proposed in [3].
4 Example
Suppose you want to implement a simple function y=x, that is, input the value of the variable x Should be passed to the output variable y. Using language 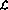 this can be encoded as (so that the "entry point" is now not the first line but the third line):
this can be encoded as (so that the "entry point" is now not the first line but the third line):
The generated perceptron network is shown in Figure 2.
The solid line represents a positive connection (weight is 1), and the dotted line represents a negative connection (weight is -1). Compared with Figure 1, the network structure is redrawn and simplified by integrating delay elements in the nodes.
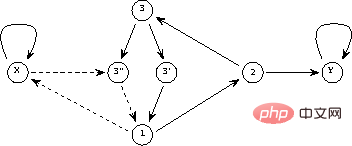
Figure 2 Network implementation of a simple program
In matrix form , the program above would look like
The first two rows/columns in matrix A correspond to the variables connected to represent the two Links to the nodes Y and X, the next three lines represent the three program lines (1, 2, and 3), and the last two represent the additional nodes required for the branch instruction (3 ' and 3'').
Then there are the initial (before iteration) and final (after iteration, when the fixed point is found) states
If the value of the variable node will be kept strictly between 0 and 1, the operation of the dynamic system (3) will be linear and the function will have no effect at all.
In principle, linear systems theory can then be used in the analysis.
For example, in FIG. 3 , the eigenvalues of the state transition matrix A are shown.
Even if there are eigenvalues outside the unit circle in the above example, the nonlinearity makes the iteration always stable.
It turns out that the iteration always converges after 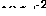 steps, where
steps, where 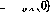 .
.
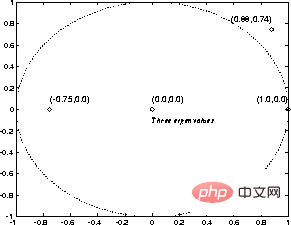
Figure 3 "Characteristic value" of a simple program
5 Discussion
5.1 Theoretical aspects
The results show that Turing machines can be encoded as perceptron networks.
By definition, all computable functions are Turing computable - within the framework of computability theory, no more powerful computational system exists.
This is why, it can be concluded -
The recurrent perceptron network (shown above) is a Turing machine (yet another) form.
The advantage of this equivalence is that the results of computability theory are easy to obtain - for example, given a network and an initial state, it is impossible to judge the process Will it eventually stop.
The above theoretical equivalence does not say anything about computational efficiency.
The different mechanisms that occur in the network can make some functions better implemented in this framework compared to traditional Turing machine implementations (which are actually today's computers).
# At least in some cases, for example, a network implementation of an algorithm can be parallelized by allowing multiple "program counters" in the snapshot vector.
The operation of the network is strictly local, not global.
An interesting question arises, for example, whether the NP-complete problem can be attacked more effectively in a network environment!
Compared to the language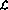 , the network implementation has the following "extensions":
, the network implementation has the following "extensions":
-
Variables Can be continuous, not just integer values. In fact, the (theoretical) ability to represent real numbers makes network implementations more powerful than the language
 , in which all numbers represented are rational numbers.
, in which all numbers represented are rational numbers.
- Various "program counters" can exist at the same time, and the transfer of control may be "fuzzy", which means that the program counter value provided by the instruction node may be a non-integer.
- A smaller extension is freely definable program entry points. This may help simplify the program - for example, the copying of variables is done in three program lines above, whereas the nominal solution (see [1]) requires seven lines and an extra local variable.
Compared with the original program code, the matrix formula is obviously a more "continuous" information representation than the program code - the parameters can be modified (often), but the iteration results are not will change suddenly.
This "redundancy" may be useful in some applications.
For example, when using a genetic algorithm (GA) for structural optimization, the random search strategy used in the genetic algorithm can be made more efficient: after the system structure changes, the continuous cost can be searched Local minima of functions use some traditional techniques (see [4]).
By learning the finite state machine structure through examples, as described in [5], it can be known that the method of iteratively enhancing the network structure is also used in this more complex situation.
Not only neural network theory may benefit from the above results - just looking at the dynamic system formula (3), it is obvious that all phenomena found in the field of computability theory are also known in simple terms Form exists - looking for non-linear dynamic processes.
For example, the undecidability of the halting problem is an interesting contribution to the field of systems theory: for any decision process represented as a Turing machine, there are dynamic systems of the form (3) that violate this process - It is not possible to construct a general stability analysis algorithm for e.g.
5.2 Related work
There are some similarities between the network structure presented and the recursive Hopfield neural network paradigm (see, e.g. [2]).
In both cases, the "input" is encoded as the initial state in the network, and the "output" is read from the final state of the network after iterations.
The fixed point of the Hopfield network is a pre-programmed pattern model, and the input is a "noise" pattern - the network can be used to enhance damaged patterns. The outlook (2) of the nonlinear function in
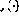 makes the number of possible states in the above-mentioned "Turing network" infinite.
makes the number of possible states in the above-mentioned "Turing network" infinite.
Compared with the Hopfield network where the unit output is always -1 or 1, it can be seen that in theory, these network structures are very different.
For example, while the set of stable points in a Hopfield network is limited, programs represented by Turing networks often have an infinite number of possible outcomes.
The computational capabilities of Hopfield networks are discussed in [6].
Petri net is a powerful tool for event-based and concurrent system modeling [7].
Petri net consists of bits and transitions and the arcs connecting them. Each place may contain any number of tokens, and the distribution of tokens is called the mark of the Petri net.
If all of a transformation's input positions are occupied by markers, the transformation may trigger, removing a marker from each input location and adding a marker to each of its output locations.
It can be proved that extended Petri nets with additional suppressing arcs also have the capabilities of Turing machines (see [7]).
The main difference between the above-mentioned Turing net and Petri net is that the framework of Petri net is more complex and has a specially customized structure, which cannot be expressed by simple general form (3).
Reference
##1 Davis, M. and Weyuker, E.: Computability, Complexity, and Languages---Fundamentals of Theoretical Computer Science. Academic Press, New York, 1983.
2 Haykin, S.: Neural Networks. A Comprehensive Foundation. Macmillan College Publishing, New York, 1994.
3 Hyötyniemi, H.: Correlations---Building Blocks of Intelligence? In Älyn ulottuvuudet ja oppihistoria (History and dimensions of intelligence), Finnish Artificial Intelligence Society, 1995, pp. 199--226.
4 Hyötyniemi, H. and Koivo, H.: Genes, Codes, and Dynamic Systems. In Proceedings of the Second Nordic Workshop on Genetic Algorithms (NWGA'96), Vaasa, Finland, August 19--23, 1996.
5 Manolios, P. and Fanelli, R.: First-Order Recurrent Neural Networks and Deterministic Finite State Automata. Neural Computation 6, 1994, pp. 1155--1173.
6 Orponen, P.: The Computational Power of Discrete Hopfield Nets with Hidden Units. Neural Computation 8, 1996 , pp. 403--415.
7 Peterson, J.L.: Petri Net Theory and the Modeling of Systems. Prentice--Hall, Englewood Cliffs, New Jersey, 1981.
Reference materials:
https://www.php.cn/link/ 0465a1824942fac19824528343613213
The above is the detailed content of Turing machine is the hottest recurrent neural network RNN in deep learning? The 1996 paper proved it!. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- Technology trends to watch in 2023
- How Artificial Intelligence is Bringing New Everyday Work to Data Center Teams
- Can artificial intelligence or automation solve the problem of low energy efficiency in buildings?
- OpenAI co-founder interviewed by Huang Renxun: GPT-4's reasoning capabilities have not yet reached expectations
- Microsoft's Bing surpasses Google in search traffic thanks to OpenAI technology


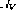 .
. 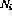 .
. 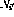 and
and 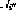 .
. 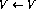 , use the following link to expand the network (assuming the node
, use the following link to expand the network (assuming the node 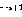 exists:
exists: 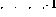 , expand the network as follows:
, expand the network as follows:  , expand the network as follows:
, expand the network as follows:  , expand the network as follows:
, expand the network as follows: