 Technology peripherals
Technology peripherals AI
AI How does ML make scientific discoveries? Oxford University's 268-page doctoral thesis details the connotation of scientific machine learning
How does ML make scientific discoveries? Oxford University's 268-page doctoral thesis details the connotation of scientific machine learningHow does ML make scientific discoveries? Oxford University's 268-page doctoral thesis details the connotation of scientific machine learning
Machine learning (ML) has caused a fundamental shift in the way we practice science, with many now making learning from data a focus of their research. As the complexity of the scientific questions we want to study increases, and as the amount of data generated by today's scientific experiments increases, ML is helping to automate, accelerate, and enhance traditional workflows. At the forefront of this revolution is a field called Scientific Machine Learning (SciML). The central goal of SciML is to more closely integrate existing scientific understanding with ML, producing powerful ML algorithms that are informed by our prior knowledge.

Paper address: https://ora.ox.ac.uk/objects/uuid:b790477c-771f- 4926-99c6-d2f9d248cb23
There are a number of methods for incorporating scientific principles into ML, and expectations are growing that SciML will solve some of the biggest challenges in science. However, the field is booming and many questions still arise. A major question is whether SciML methods can be extended to more complex real-world problems. Much SciML research is in the proof-of-concept stage, where the technology is tested on reduced, simple problems. However, understanding their scalability to more complex problems is critical for their widespread application. This question is the central one of this article.
#First, a variety of different physics knowledge machines are designed for three complex, real-world, domain-specific case studies in lunar science and geophysics learning methods and evaluate their performance and scalability. Second, the scalability of physics-informed neural networks, a popular general-purpose SciML method, for solving differential equations with large regions and high-frequency solutions is evaluated and improved. Common observations from these studies are discussed and significant advantages and potential limitations are identified, highlighting the importance of designing scalable SciML techniques.
Introduction
Machine learning (ML) has caused a revolution in the field of science. Traditionally, scientific research revolves around theory and experiment: one proposes a handcrafted and well-defined theory, then continuously refines it using experimental data, and analyzes it to make new predictions. But today, many people are making learning from data a focus of their research. Here, a model of the world is learned from data via ML algorithms, and existing theory is not needed. This shift occurs for a variety of reasons.
#First of all, the ML field has experienced exponential growth over the past decade, and the main driver behind this surge is often attributed to the breakthrough of deep learning. [Goodfellow et al., 2016]. Important discoveries such as the use of deeper network designs and better training algorithms, as well as the availability of more powerful computing architectures, have led to rapid improvements in the performance of deep learning techniques on a wide range of problems [Dally et al., 2021] . Modern ML algorithms are now capable of learning and solving incredibly complex tasks, from self-driving cars [Schwarting et al., 2018] to beating world-class Go players [Silver et al., 2018].
#With these advances, today’s scientific experiments generate more and more data and study increasingly complex phenomena [Baker et al., 2019 , Hey et al., 2020]. Analyzing and theorizing about all this data is quickly becoming impossible for humans and our traditional workflows, and soon scientific experiments may well be limited by their ability to extract insights from the data they already have, rather than what they can collect. What data [Baker et al., 2019]. Given the powerful tools ML can provide, many researchers are turning to ML to help automate, accelerate, and enhance traditional workflows. Over the past decade, the combination of new ML algorithms and data availability has led to some major scientific advances. For example, ML has been used to predict protein structures more accurately than ever before [Jumper et al., 2021], synthesize speech from neural activity [anummanchipalli et al., 2019], and improve simulations of quantum many-body systems [ Carleo and Troyer, 2017]. In fact, modern ML algorithms are now applied to almost every aspect of science, and one of the defining research questions of this era has become: "Solve problem X and apply ML to it", followed by Interesting and often exciting results.
However, despite these advances, various shortcomings of ML, especially deep learning algorithms, have materialized in the ML field. For example, despite their ability to learn highly complex phenomena, deep neural networks are often viewed as "black boxes" with a lack of understanding of how they represent and reason about the world. This uninterpretability is a critical issue, especially for safety-critical applications that require demonstration of network predictions [Gilpin et al., 2019, Castelvecchi, 2016]. Furthermore, there is little theoretical guidance on how to design deep learning algorithms suitable for specific tasks. The choice of deep neural network architecture is largely empirical, although the fields of meta-learning and neural architecture search are starting to provide more automated approaches [Elsken et al., 2019, Hospedales et al., 2021]. Finally, although deep neural networks are highly expressive, they are limited by the training data and often perform poorly outside the training distribution. Learning generalizable models of the world that perform well on new tasks is a key feature of more general artificial intelligence (AI) systems and a key outstanding challenge in the field of ML [Bengio et al., 2021].
Researchers begin to encounter these limitations when using ML in scientific problems [Ourmazd, 2020, Forde and Paganini, 2019]. Given the poor generalization capabilities of deep neural networks, a key question is whether they actually "learn" scientific principles. A good scientific theory is expected to make novel and accurate predictions outside of experimental data, but deep neural networks have difficulty making accurate predictions outside of training data. Even if a network can make reliable predictions, extracting any meaningful scientific insights from them can be challenging given their uninterpretability.
#Another major problem is that many current machine learning workflows completely replace traditional scientific models with learned models. While this can be useful, these purely data-driven methods "throw away" a large amount of our prior scientific knowledge.
#The important point is that for many problems there is an existing theory to build on rather than starting from scratch. In a field that has traditionally been based on a tight interplay between explicit theory and experiment, some argue that the above limitations make current ML methods unacceptable. These concerns have spurred the formation of a rapidly growing new field called Scientific Machine Learning (SciML) [Baker et al., 2019, Karniadakis et al., 2021, Willard et al., 2020, Cuomo et al., 2022, Arridge et al., 2019, Karpatne et al., 2017a]. The goal of SciML is to fuse existing scientific knowledge and ML to generate more nuanced ML algorithms that are informed by our prior knowledge, as shown in Figure 1.1. The key argument in this area is that by doing this we will ultimately achieve more robust methods for doing scientific research. Traditional methods and ML methods each have their own advantages and disadvantages, and a combination of the two may be more effective than either one. For example, when doing data assimilation (such as in climate models), traditional physical models can be used to provide prior knowledge, while ML can be used to account for data dependencies and other unknown physics.

Figure 1.1: Overview of Scientific Machine Learning (SciML). SciML aims to tightly integrate ML with scientific knowledge in order to generate more powerful, robust and interpretable ML methods for scientific research.
#Expectations in this field are growing rapidly, and a large number of methods and many innovative strategies are currently being proposed and studied to incorporate scientific knowledge into ML. These methods range from intended scientific tasks (such as simulation, inversion and governing equation discovery), to different ways to incorporate scientific principles (such as through the architecture of deep neural networks, their loss functions and the use of hybrid models), and scientific The extent to which principles are imposed (e.g., through hard or soft constraints). We will review these methods in detail in Chapter 2. Many methods use ideas from physics to inform their ML algorithms in a subfield of SciML called physically-informed machine learning (PIML) [Karniadakis et al., 2021].
So far, SciML has had some initial success. It helps us perform powerful simulations [Raissi al., 2019], discover the governing equations of complex physical systems [Kutz and Brunton, 2022], and accurately invert fundamental parameters in inversion problems [Arridge et al., 2019] , and seamlessly integrate traditional workflows with learned components across a wide range of domains [Rackauckas et al., 2020, Thuerey et al., 2021]. Despite early promise, the field of SciML is still in its infancy and many important questions arise, such as; how should we implement scientific principles? How should we balance the lack of interpretability of data-driven models with the clarity of existing theory? ?Is there an overarching SciML technology that can be applied across scientific disciplines? Can SciML provide new perspectives and ideas for the ML field? How scalable is SciML technology for complex real-world problems? This article mainly studies the last question, The specific discussion is as follows.
#In this paper, we mainly use two methods to study the above sub-problems. First, for the first three sub-problems, complex, real-life, domain-specific case studies are used to examine the performance and scalability of multiple different PIML methods. For each subproblem, we present a case study, propose a PIML technique (or various PIML techniques) to solve it, and evaluate how the technique can be extended to this setting. Second, for the last sub-problem, we focus on a single general-purpose PIML technology and evaluate and improve its scalability. The first three sub-problems are studied in separate chapters of this thesis (Chapter 3 ~ 5 respectively), and their case studies are all from the fields of lunar science and geophysics. The last sub-problem will be studied in Chapter 6. Finally, we discuss and summarize the implications of each chapter for our main research questions in Chapter 7.
Genealogy of SciML methods. This graph shows how “strong” the different types of SciML methods introduced in this chapter are for scientific knowledge. Note that the strength of a scientific constraint is a rather vague concept; in this diagram, we define it as how close a SciML approach is to a traditional workflow. Intermediate approaches also combine ML with certain aspects of traditional workflows, such as in looping methods that interweave traditional iterative solvers with ML models. Also, our assignment is somewhat subjective, so this number is just to express the general trend.



The above is the detailed content of How does ML make scientific discoveries? Oxford University's 268-page doctoral thesis details the connotation of scientific machine learning. For more information, please follow other related articles on the PHP Chinese website!
 Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AM
Are You At Risk Of AI Agency Decay? Take The Test To Find OutApr 21, 2025 am 11:31 AMThis article explores the growing concern of "AI agency decay"—the gradual decline in our ability to think and decide independently. This is especially crucial for business leaders navigating the increasingly automated world while retainin
 How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AM
How to Build an AI Agent from Scratch? - Analytics VidhyaApr 21, 2025 am 11:30 AMEver wondered how AI agents like Siri and Alexa work? These intelligent systems are becoming more important in our daily lives. This article introduces the ReAct pattern, a method that enhances AI agents by combining reasoning an
 Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM
Revisiting The Humanities In The Age Of AIApr 21, 2025 am 11:28 AM"I think AI tools are changing the learning opportunities for college students. We believe in developing students in core courses, but more and more people also want to get a perspective of computational and statistical thinking," said University of Chicago President Paul Alivisatos in an interview with Deloitte Nitin Mittal at the Davos Forum in January. He believes that people will have to become creators and co-creators of AI, which means that learning and other aspects need to adapt to some major changes. Digital intelligence and critical thinking Professor Alexa Joubin of George Washington University described artificial intelligence as a “heuristic tool” in the humanities and explores how it changes
 Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AM
Understanding LangChain Agent FrameworkApr 21, 2025 am 11:25 AMLangChain is a powerful toolkit for building sophisticated AI applications. Its agent architecture is particularly noteworthy, allowing developers to create intelligent systems capable of independent reasoning, decision-making, and action. This expl
 What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AM
What are the Radial Basis Functions Neural Networks?Apr 21, 2025 am 11:13 AMRadial Basis Function Neural Networks (RBFNNs): A Comprehensive Guide Radial Basis Function Neural Networks (RBFNNs) are a powerful type of neural network architecture that leverages radial basis functions for activation. Their unique structure make
 The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AM
The Meshing Of Minds And Machines Has ArrivedApr 21, 2025 am 11:11 AMBrain-computer interfaces (BCIs) directly link the brain to external devices, translating brain impulses into actions without physical movement. This technology utilizes implanted sensors to capture brain signals, converting them into digital comman
 Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AM
Insights on spaCy, Prodigy and Generative AI from Ines MontaniApr 21, 2025 am 11:01 AMThis "Leading with Data" episode features Ines Montani, co-founder and CEO of Explosion AI, and co-developer of spaCy and Prodigy. Ines offers expert insights into the evolution of these tools, Explosion's unique business model, and the tr
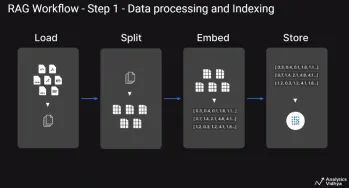 A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AM
A Guide to Building Agentic RAG Systems with LangGraphApr 21, 2025 am 11:00 AMThis article explores Retrieval Augmented Generation (RAG) systems and how AI agents can enhance their capabilities. Traditional RAG systems, while useful for leveraging custom enterprise data, suffer from limitations such as a lack of real-time dat


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

Atom editor mac version download
The most popular open source editor

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

Zend Studio 13.0.1
Powerful PHP integrated development environment





