18 pictures to intuitively understand neural networks, manifolds and topology

To date, one of the major concerns about neural networks is that they are black boxes that are difficult to explain. This article mainly theoretically understands why neural networks are so effective at pattern recognition and classification. Its essence is to distort and deform the original input through layers of affine transformation and nonlinear transformation until it can be easily distinguished into different categories. . In fact, the back propagation algorithm (BP) actually continuously fine-tunes the distortion effect based on the training data.

Beginning about ten years ago, deep neural networks have achieved breakthrough results in fields such as computer vision, arousing great interest and attention.

However, some people are still worried. One reason is that a neural network is a black box: if a neural network is trained well, high-quality results can be obtained, but it is difficult to understand how it works. If a neural network malfunctions, it can be difficult to pinpoint the problem.

Although it is difficult to understand deep neural networks as a whole, you can start with low-dimensional deep neural networks, that is, networks with only a few neurons in each layer, which are much easier to understand. We can understand the behavior and training of low-dimensional deep neural networks through visualization methods. Visualization methods allow us to understand the behavior of neural networks more intuitively and observe the connection between neural networks and topology.

I'll talk about a lot of interesting things next, including the lower bound on complexity of a neural network capable of classifying a specific data set.

1. A simple example

Let us start with a very simple data set. In the figure below, two curves on the plane are composed of countless points. The neural network will try to distinguish which line these points belong to.

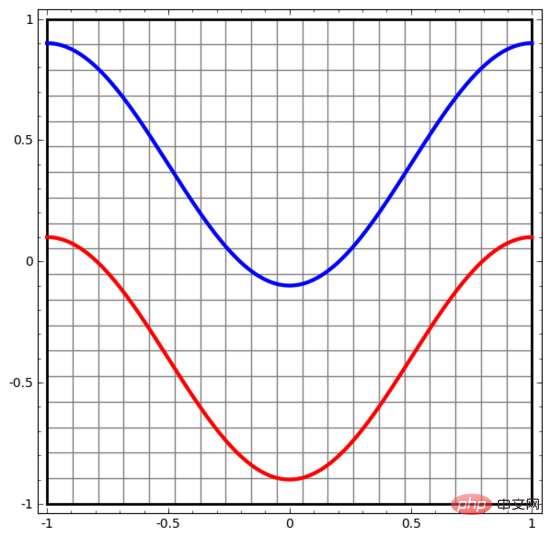
The most straightforward way to observe the behavior of a neural network (or any classification algorithm) is to see how it classifies each data point.

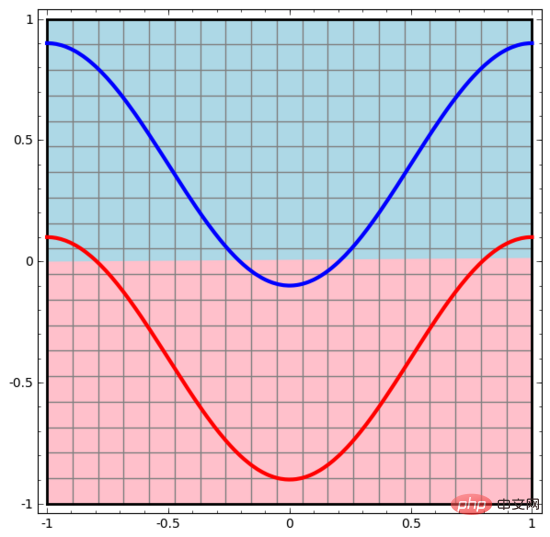
We start with the simplest neural network, which has only one input layer and one output layer. Such a neural network simply separates two types of data points with a straight line.

Such a neural network is too simple and crude. Modern neural networks often have multiple layers between the input and output layers, called hidden layers. Even the simplest modern neural network has at least one hidden layer.

A simple neural network, picture source Wikipedia

Similarly, we observe what the neural network does for each data point. As can be seen, this neural network uses a curve instead of a straight line to separate data points. Obviously, curves are more complex than straight lines.

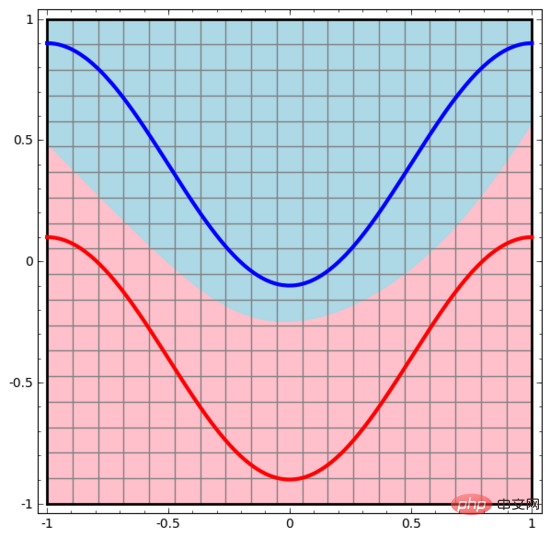
# Each layer of the neural network uses a new representation to represent the data. We can observe how the data is transformed into new representations and how the neural network classifies them. In the last layer of representation, the neural network draws a line between the two types of data (or a hyperplane if in higher dimensions).

In the previous visualization, we saw the original representation of the data. You can think of it as what the data looks like in the "input layer". Now let's look at what the data looks like after it has been transformed. You can think of it as what the data looks like in the "hidden layer".

Each dimension of the data corresponds to the activation of a neuron in the neural network layer.

The hidden layer uses the above method to represent the data, so that the data can be separated by a straight line (that is, linearly separable)

2. Continuous visualization of layers

In the method of the previous section, each layer of the neural network uses different representations to represent data. In this way, the representations of each layer are discrete and not continuous.

This creates difficulties in our understanding. How to convert from one representation to another? Fortunately, the characteristics of the neural network layer make it very easy to understand this aspect.

There are various different layers in a neural network. Below we will discuss the tanh layer as a specific example. A tanh layer, including:

• Use the "weight" matrix W for linear transformation
• Use vector b for translation
• Use tanh to represent point by point

We can think of it as a continuous transformation as follows:

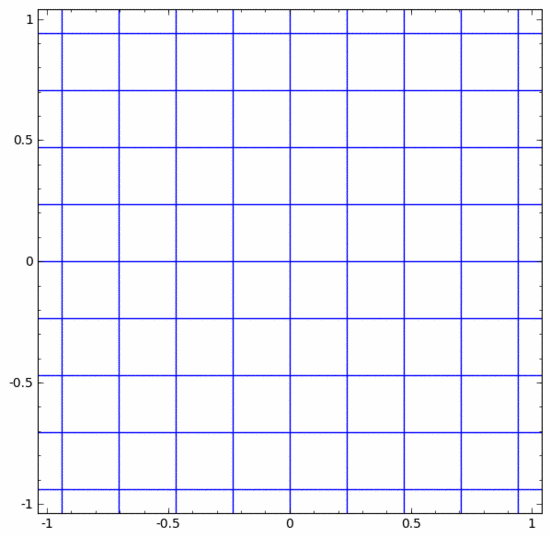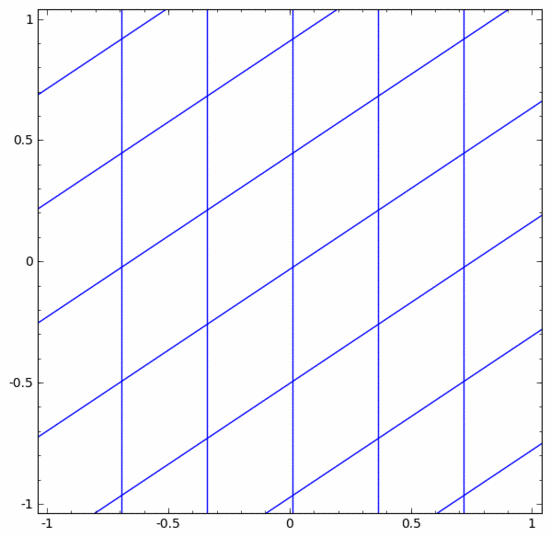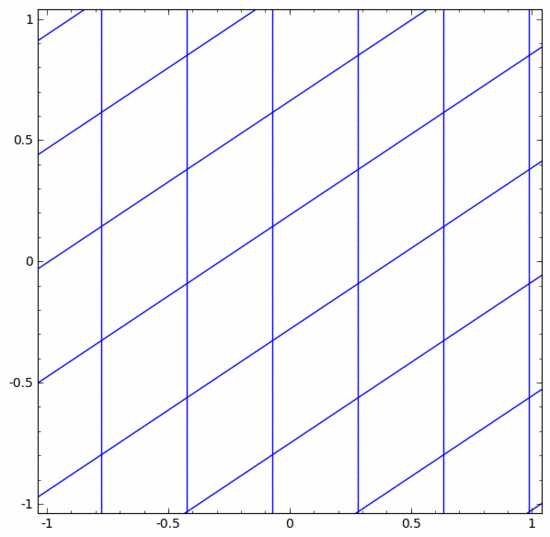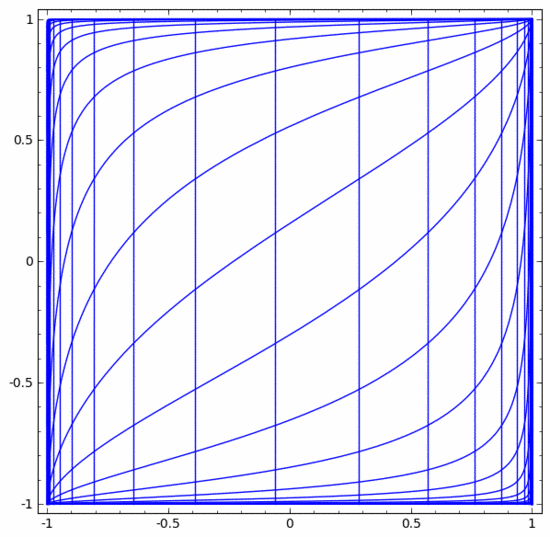
The situation is much the same for other standard layers, consisting of point-wise application of affine transformations and monotonic activation functions.

We can use this method to understand more complex neural networks. For example, the neural network below uses four hidden layers to classify two slightly intertwined spirals. It can be seen that in order to classify the data, the representation of the data is continuously transformed. The two spirals are initially entangled, but eventually they can be separated by a straight line (linearly separable).

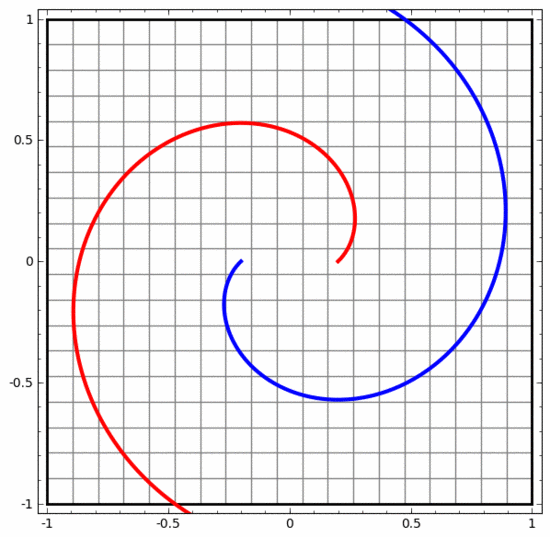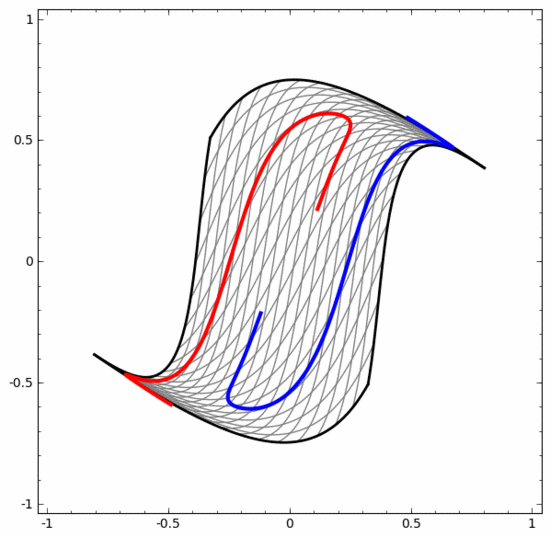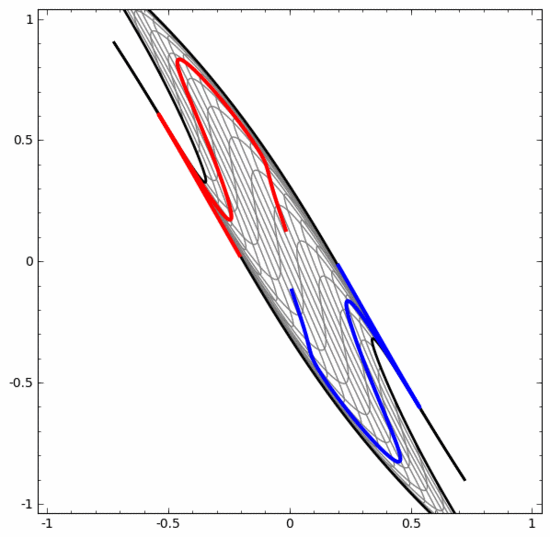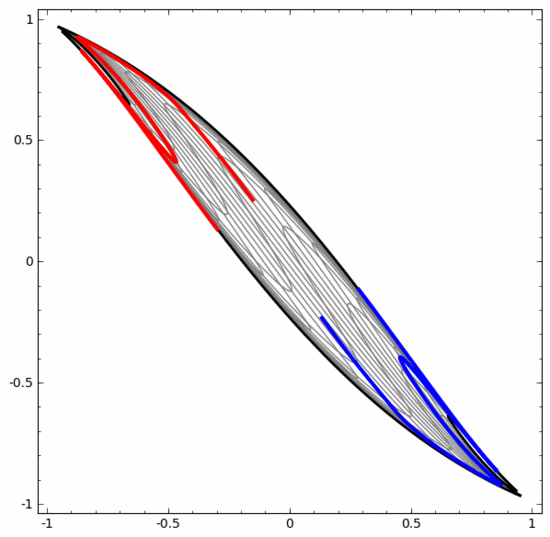
On the other hand, the neural network below, although it also uses multiple hidden layers, cannot divide two more deeply intertwined spirals.

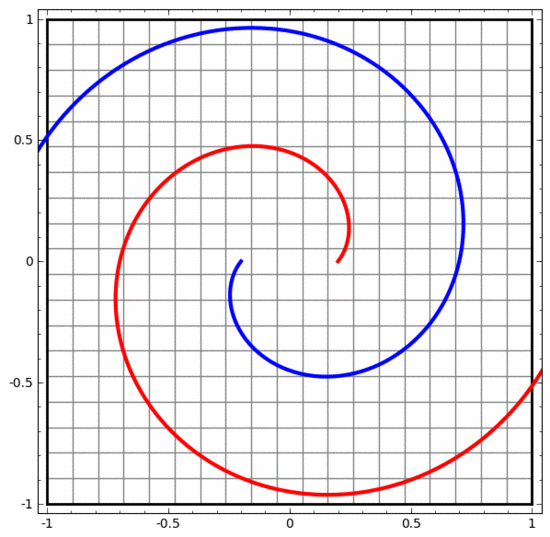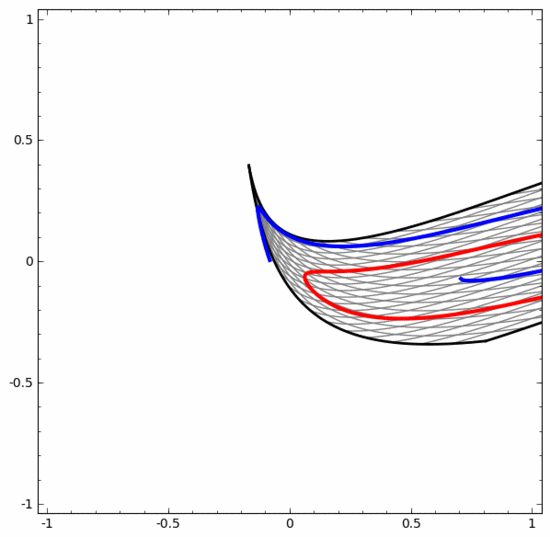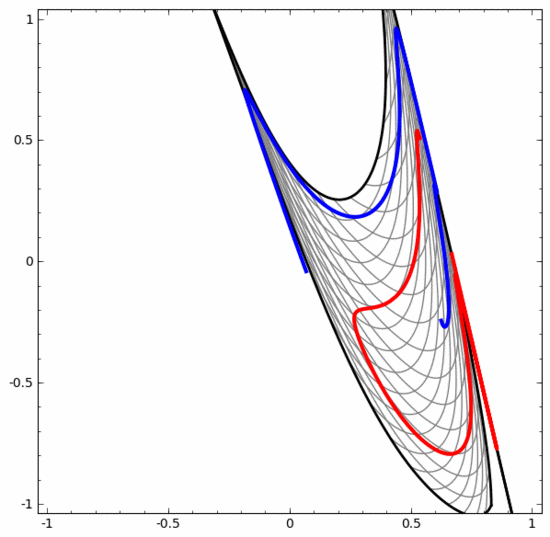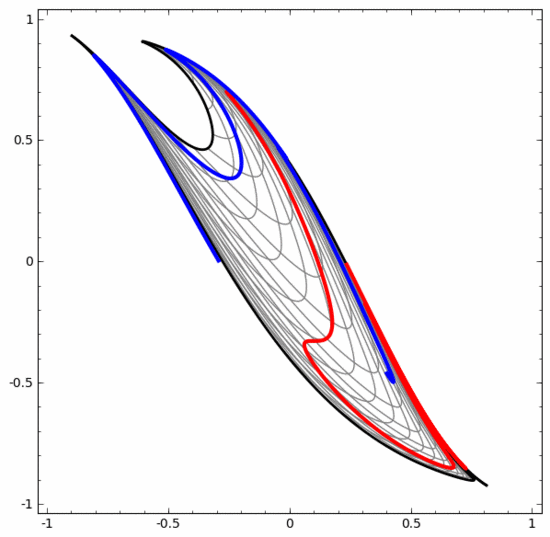
It should be clearly pointed out that the above two spiral classification tasks have some challenges because we are currently using only low-dimensional neural networks. Everything would be much easier if we used a wider neural network.

(Andrej Karpathy made a good demo based on ConvnetJS, which allows people to interactively explore neural networks through this kind of visual training.)

3. Topology of tanh layer

Each layer of a neural network stretches and squeezes space, but it does not shear, split, or fold space. Intuitively, neural networks do not destroy the topological properties of the data. For example, if a set of data is continuous, then its transformed representation will also be continuous (and vice versa).

Transformations like this that do not affect topological properties are called homeomorphisms. Formally, they are bijections of bidirectional continuous functions.

Theorem: If the weight matrix W is non-singular, and a layer of the neural network has N inputs and N outputs, then the mapping of this layer is homeomorphic (for a specific domain and value range).

Proof: Let’s do it step by step:

1. Suppose W has a non-zero determinant. Then it is a bilinear linear function with a linear inverse. Linear functions are continuous. Then the transformation such as "multiplying by W" is homeomorphism;

2. The "translation" transformation is homeomorphism;

3. tanh (there are also sigmoid and softplus, but not ReLU ) is a continuous function with continuous inverses. (for a particular domain and range), they are bijections, and their pointwise application is homeomorphism.

Therefore, if W has a non-zero determinant, this neural network layer is homeomorphic.

If we randomly combine such layers together, this result still holds.

4. Topology and Classification

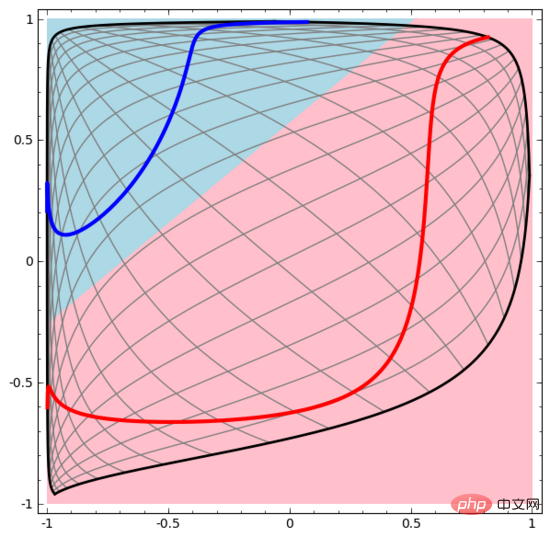
Let’s look at a two-dimensional data set, which contains two types of data A and B:

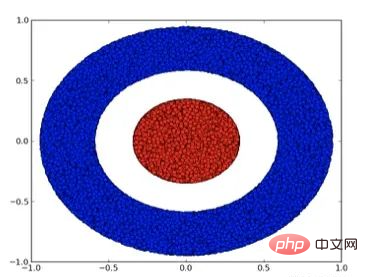
A is red, B is blue

Description: To classify this data set, the neural network (regardless of depth) must have a hidden unit containing 3 or more layer.

As mentioned before, using sigmoid units or softmax layers for classification is equivalent to finding a hyperplane (in this case, a straight line) in the representation of the last layer to separate A and B. With only two hidden units, the neural network is topologically unable to separate the data in this way, and thus cannot classify the above dataset.

In the visualization below, the hidden layer transforms the representation of the data, with straight lines as dividing lines. It can be seen that the dividing line continues to rotate and move, but it is never able to separate the two types of data A and B well.

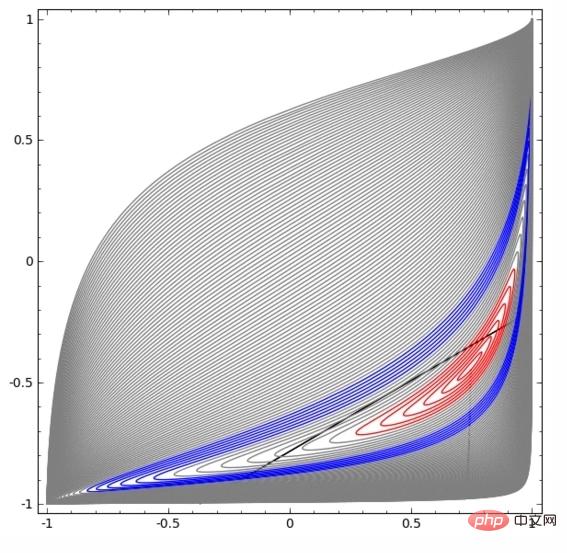
No matter how well trained a neural network is, it cannot complete the classification task well

In the end, it can only barely achieve a local minimum, reaching 80% classification accuracy.

The above example only has one hidden layer, and since there are only two hidden units, it will fail to classify anyway.

Proof: If there are only two hidden units, either the transformation of this layer is homeomorphic, or the weight matrix of the layer has determinant 0. If it is homeomorphism, A is still surrounded by B, and A and B cannot be separated by a straight line. If there is a determinant of 0, then the data set will be collapsed on some axis. Because A is surrounded by B, folding A on any axis will cause some of the A data points to be mixed with B, making it impossible to distinguish A from B.

But if we add a third hidden unit, the problem is solved. At this time, the neural network can convert the data into the following representation:

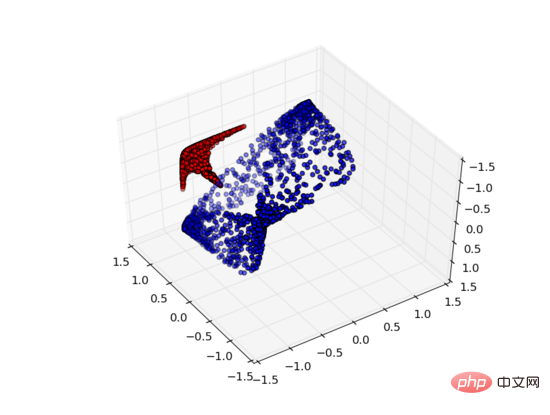
#At this time, a hyperplane can be used to separate A and B.

In order to better explain its principle, here is a simpler one-dimensional data set as an example:

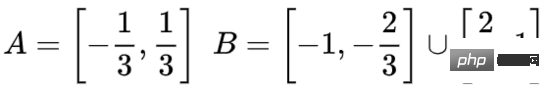
To classify this dataset, a layer consisting of two or more hidden units must be used. If you use two hidden units, you can represent the data with a nice curve, so that you can separate A and B with a straight line:

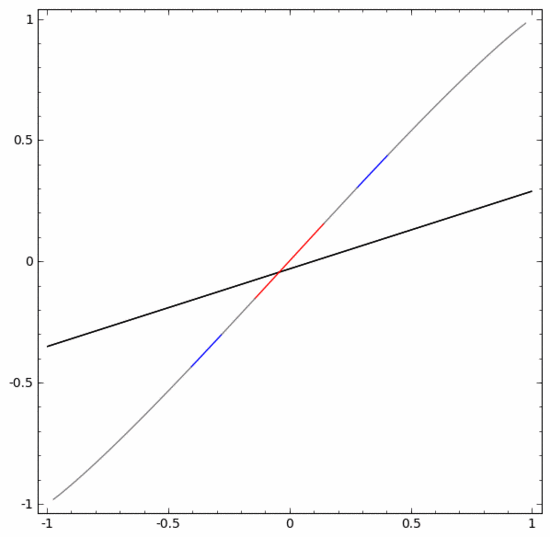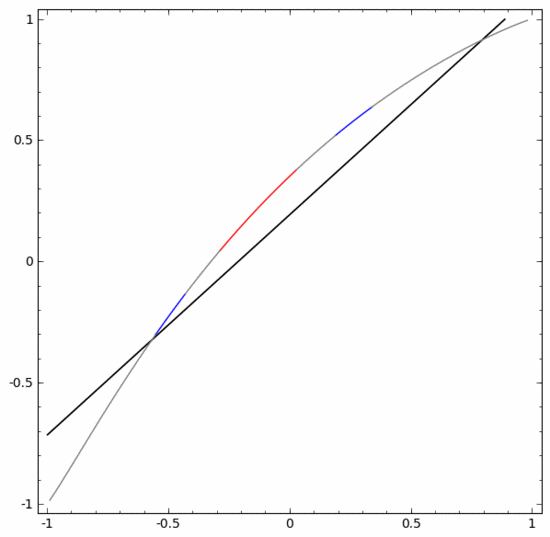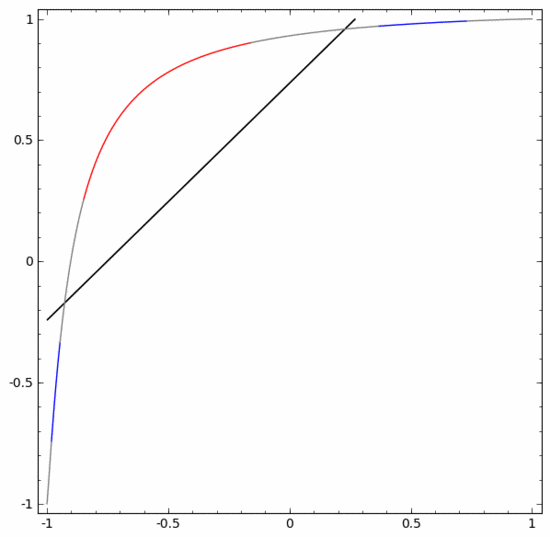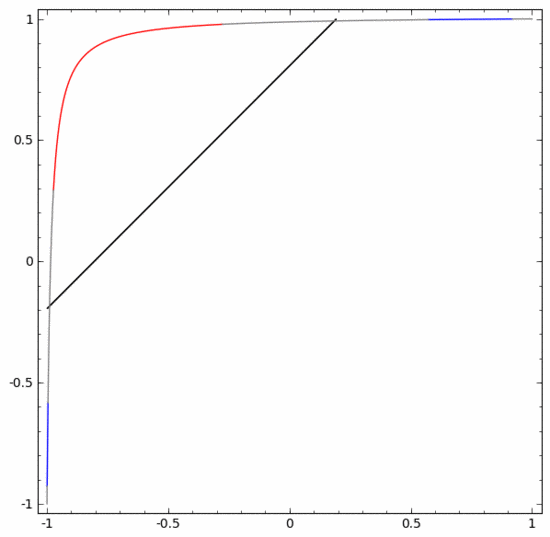
How to do it What about? When , one of the hidden units is activated; when , the other hidden unit is activated. When the previous hidden unit is activated and the next hidden unit is not activated, it can be judged that this is a data point belonging to A.

5. Manifold hypothesis

Does the manifold hypothesis make sense for processing real-world data sets (such as image data)? I think it makes sense.

The manifold hypothesis means that natural data forms a low-dimensional manifold in its embedding space. This hypothesis has theoretical and experimental support. If you believe in the manifold hypothesis, then the task of a classification algorithm boils down to separating a set of entangled manifolds.

In the previous example, one class completely surrounded another class. However, in real-world data, it is unlikely that the dog image manifold will be completely surrounded by the cat image manifold. However, other more reasonable topological situations may still cause problems, as will be discussed in the next section.

6. Links and homotopy

Next I will talk about another interesting data set: two mutually linked torus (tori), A and B.

Similar to the data set situation we talked about before, you cannot separate an n-dimensional data set without using n 1 dimensions (n ​​1 dimensions in this case That is the 4th dimension).

The link problem belongs to the knot theory in topology. Sometimes, when we see a link, we cannot immediately tell whether it is a broken link (unlink means that although they are entangled with each other, they can be separated through continuous deformation).

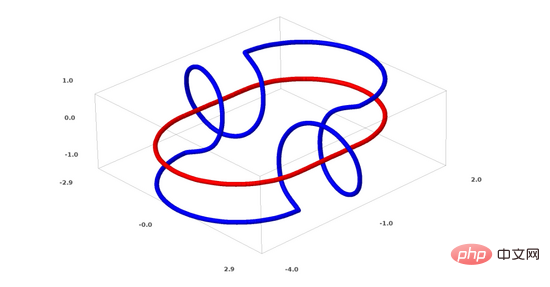
A simpler broken link

If a neural network with only 3 hidden units in the hidden layer can classify a data set, then this data set It is a broken link (the question is: theoretically, can all broken links be classified by a neural network with only 3 hidden units?).

From a knot theory perspective, the continuous visualization of data representations produced by neural networks is not only a nice animation, but also a process of unraveling links. In topology, we call this the ambient isotopy between the original link and the separated link.

The surrounding homeomorphism between manifold A and manifold B is a continuous function:

Each is a homeomorphism of X. is the characteristic function, mapping A to B. That is, constantly transitioning from mapping A to itself to mapping A to B.

Theorem: If the following three conditions are met at the same time: (1) W is non-singular; (2) the order of neurons in the hidden layer can be manually arranged; (3) the number of hidden units is greater than 1, then the input of the neural network There is a wraparound similarity between representations produced by neural network layers.

Proof: We also go step by step:

1. The hardest part is the linear conversion. To achieve a linear transformation, we need W to have a positive determinant. Our premise is that the determinant is non-zero, and if the determinant is negative, we can turn it into positive by swapping two hidden neurons. The space of the positive determinant matrix is ​​path-connected, so there is 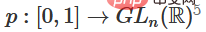, therefore, 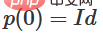, 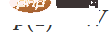. With the function 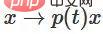, we can continuously transition the eigenfunction to the W transformation, multiplying x with the matrix of the continuous transition at each point at time t.

2. You can transition from the characteristic function to b translation through the function .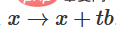

3. You can transition from the characteristic function to the point-by-point application through the function .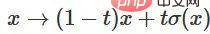

I guess someone may be interested in the following question: Can a program be developed that can automatically discover such ambient isotopy, and can also automatically prove the equivalence of some different links or Separability of certain links. I also want to know whether neural networks can beat the current SOTA technology in this regard.

Although the form of linking we are talking about now will probably not appear in real-world data, there may be higher-dimensional generalizations in real-world data.

Links and knots are both 1-dimensional manifolds, but 4 dimensions are needed to separate them. Similarly, to separate an n-dimensional manifold, a higher-dimensional space is needed. All n-dimensional manifolds can be separated by 2n 2 dimensions.

7. A simple method

For neural networks, the simplest method is to directly pull apart the intertwined manifolds, and pull out the entangled parts. The finer the better. Although this is not the fundamental solution we are pursuing, it can achieve relatively high classification accuracy and achieve a relatively ideal local minimum.

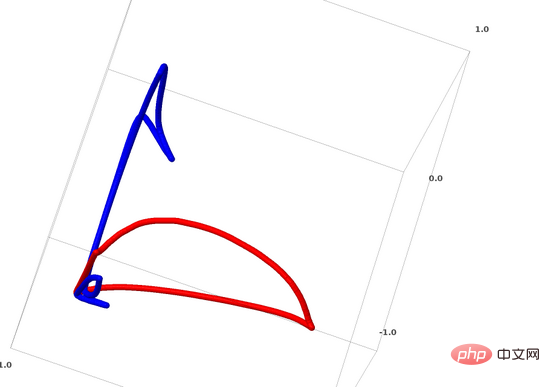
This approach will result in very high derivatives in the area you are trying to stretch. To deal with this, you need to use a shrinkage penalty, which penalizes the derivative of the layer of data points.

Local minima are not useful for solving topological problems, but topological problems may provide good ideas for exploring and solving the above problems.

On the other hand, if we only care about getting good classification results, is it a problem for us if a small part of the manifold is entangled with another manifold? If we only care about the classification results, then this doesn't seem to be a problem.

(My intuition is that taking shortcuts like this is not good and can easily lead to a dead end. In particular, in optimization problems, seeking local minima does not really solve the problem, and if you choose a A solution that cannot truly solve the problem will ultimately fail to achieve good performance.)

8. Choose a neural network layer that is more suitable for manipulating manifolds?

I think that standard neural network layers are not suitable for manipulating manifolds because they use affine transformations and point-wise activation functions.

Perhaps we can use a completely different neural network layer?

One idea that comes to mind is, first, let the neural network learn a vector field whose direction is the direction we want to move the manifold:

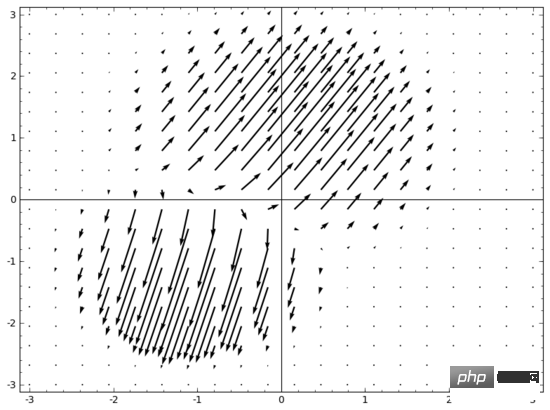
Then deform the space based on this:

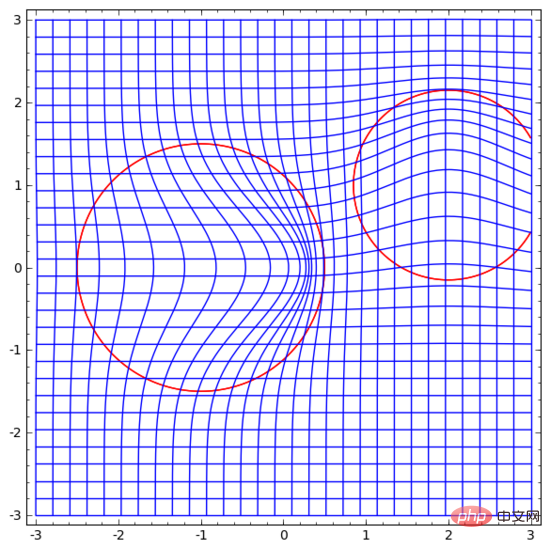
We can learn vector fields at fixed points (just pick some fixed points from the training set as anchors), and Interpolate in some way. The form of the above vector field is as follows:

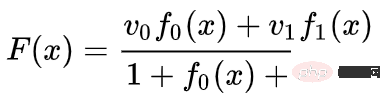
where and are vectors, and are n-dimensional Gaussian functions. This idea is inspired by radial basis functions.

9. K-Nearest Neighbor Layer

My other point of view is that linear separability may be an excessive and unreasonable requirement for neural networks, perhaps using k nearest neighbors (k-NN) would be better. However, the k-NN algorithm relies heavily on the representation of data. Therefore, a good data representation is required for the k-NN algorithm to achieve good results.

In the first experiment, I trained some MNIST neural networks (two-layer CNN, no dropout) with an error rate below 1%. Then, I discarded the last softmax layer and used the k-NN algorithm, and multiple times the results showed that the error rate was reduced by 0.1-0.2%.

However, I feel that this approach is still wrong. The neural network is still trying to linearly classify, but due to the use of the k-NN algorithm, it can slightly correct some of the errors it makes, thereby reducing the error rate.

Due to the (1/distance) weighting, k-NN is differentiable to the data representation it acts on. Therefore, we can directly train the neural network for k-NN classification. This can be thought of as a "nearest neighbor" layer, which acts similarly to a softmax layer.

We don’t want to feed back the entire training set for each mini-batch because it is too computationally expensive. I think a good approach would be to classify each element in the mini-batch based on the category of the other elements in the mini-batch, giving each element a weight of (1/(distance from the classification target)).

Unfortunately, even with complex architectures, using the k-NN algorithm can only reduce the error rate to 4-5%, while using simple architectures the error rate is higher. However, I didn’t put much effort into the hyperparameters.

But I still like the k-NN algorithm because it is more suitable for neural networks. We want points on the same manifold to be closer to each other, rather than insisting on using hyperplanes to separate the manifolds. This amounts to shrinking a single manifold while making the space between manifolds of different categories larger. This simplifies the problem.

10. Summary

Certain topological characteristics of the data may cause these data to be unable to be linearly separated using low-dimensional neural networks (regardless of the depth of the neural network). Even where it is technically feasible, such as spirals, separation is very difficult to achieve with low-dimensional neural networks.

To accurately classify data, neural networks sometimes require wider layers. In addition, traditional neural network layers are not suitable for manipulating manifolds; even if the weights are set manually, it is difficult to obtain an ideal data transformation representation. New neural network layers may be able to play a good supporting role, especially new neural network layers inspired by understanding machine learning from a manifold perspective.

The above is the detailed content of 18 pictures to intuitively understand neural networks, manifolds and topology. For more information, please follow other related articles on the PHP Chinese website!