Home >Technology peripherals >AI >A brief discussion on graph embedding algorithms
A brief discussion on graph embedding algorithms
- 王林forward
- 2023-04-12 17:52:062662browse

Part 01
##● ##What is graph embedding ●
Graph embedding is the process of mapping graph structure data into low-dimensional dense vectors. At the same time, nodes with similar topological structures or close attributes in the original graph are also close in position in the vector space, which can be easily It effectively solves the problem of difficulty in efficiently inputting graph-structured data into machine learning algorithms.
#For the representation and storage of graphs, the easiest way to think of is to use an adjacency matrix. Number each node in the graph to construct a matrix of  , where
, where 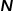 represents the The number of nodes. Whether any two nodes in the graph are connected by an edge determines the value of the corresponding position in the adjacency matrix. This representation method is very easy to understand and intuitive, but it is very inefficient. Because graphs in real-life scenarios may contain thousands or even more nodes, and most nodes are not connected by edges, this will cause the resulting adjacency matrix to be very sparse. Using adjacency matrices to represent and store graphs requires high computational and space costs, while graph embedding algorithms can efficiently solve graph analysis problems.
represents the The number of nodes. Whether any two nodes in the graph are connected by an edge determines the value of the corresponding position in the adjacency matrix. This representation method is very easy to understand and intuitive, but it is very inefficient. Because graphs in real-life scenarios may contain thousands or even more nodes, and most nodes are not connected by edges, this will cause the resulting adjacency matrix to be very sparse. Using adjacency matrices to represent and store graphs requires high computational and space costs, while graph embedding algorithms can efficiently solve graph analysis problems.
Part 02
##●Basic concepts ●
Concept 1 Picture:The graph is represented as Concept 2 Isomorphic graph: Graph Concept 3 Heterogeneous graph: Graph Concept 4 First-order similarity: If the weight of the edge connecting two nodes is larger, the first-order similarity between them is larger. The first-order similarity between node Concept 5 Second-order similarity: If two nodes are adjacent to the network The more similar the structures are, the greater the second-order similarity between them. The second-order similarity between node Figure 1 Second-order similarity diagram Concept 6 Figure embedding: Given an input graph and a predefined embedding dimension, graph embedding is to transform the graph into a dimensional space while retaining the graph properties as much as possible. Relying on first-order similarity or higher-order similarity to quantify the degree of preservation of graph attributes, using a dimensional vector or a set of ##Part 03 ##● Graph embedding algorithm classification ##● (1) Node embedding (2) Edge embedding Use vectors to map graphs in low-dimensional space Each edge in is represented. An edge consists of a pair of nodes and usually represents a node-pair relationship. Edge embedding is suitable when you need to analyze the edges in the graph and perform tasks such as knowledge graph relationship prediction or link prediction. (3) Graph embedding Use vectors in low-dimensional space to embed the entire A representation is represented by a diagram, usually a small diagram such as a molecule or protein. Representing a graph as a vector facilitates calculation of similarities between different graphs, thereby solving graph classification problems. Different task requirements determine the graph embedding algorithm selected. Due to space reasons, the DeepWalk algorithm and Node2Vec algorithm in node embedding are excerpted here to compare Detailed study.
Part 04##● Classic graph embedding algorithm ● 1.DeepWalk algorithm Inspired by word2vec ideas in the field of natural language processing, Perozzi et al. In the model of node representation vector, the co-occurrence relationship between nodes is analogized to the co-occurrence relationship between words in the corpus, and the DeepWalk algorithm is proposed. The sequence of neighbor nodes of nodes in the graph is collected through random walks, which is equivalent to a corpus of node context, and can thus solve the problem of extracting co-occurrence relationships between nodes in the graph. Set the length and starting point of the node sequence in advance. The random walk strategy will guide how to determine the next walking node among neighbor nodes. Repeat this step to obtain a sequence that meets the conditions. The random walk diagram is shown in Figure 2. Show.
Figure 2 Schematic diagram of random walk The words in the word2vec algorithm correspond to The node In order to further learn the latent feature representation of nodes, the DeepWalk algorithm introduces a mapping function The calculation of probability also needs to refer to the skip-gram model in the word2vec algorithm. As shown in Figure 3, the skip-gram model contains two key matrices, one is the center word vector matrix In the random walk process, the sequential relationship between nodes in the sampling sequence is not considered, which can be better It reflects the proximity relationship of nodes effectively and reduces the calculation cost. ##Figure 3 Skip-gram model diagram 2.Node2Vec algorithm Based on the DeepWalk algorithm, researchers Grover A and Leskovec J proposed the Node2Vec algorithm. The Node2Vec algorithm optimizes the process of generating node sequences through random walks in the DeepWalk algorithm, defining parameters ##where represents the slave node ##Figure 4 Node2Vec random walk strategy diagram Node2Vec’s random walk strategy is controlled based on two parameters, as shown in Figure 4. Assume that node v is reached through edge When the walking sample goes from node (1) When (2) When (3) When In other words, the parameter Part 05 ##● ##Summary ##● With the rapid development of information technology, the network environment has become increasingly complex, and network attacks occur frequently. Among them, APT attacks are at a high rate, which is a security issue that enterprises need to pay attention to. In fact, the basic environment in which APT attacks occur - the network itself is a network structure composed of computers and other elements. It is not difficult to think of using graph data structures to express the relationship between these elements, and then transform the attack detection problem into Node, edge or subgraph classification task in a graph. Graph embedding is a rich issue with great research space. How to improve model training efficiency, innovate model construction methods, and apply the idea of graph embedding to more production practices. Enterprises need further research to find better solutions. Answer. References [1]Xu M. Understanding graph embedding methods and their applications[J]. SIAM Review, 2021, 63(4): 825-853. [2]Cai H, Zheng V W, Chang K C C . A comprehensive survey of graph embedding: Problems, techniques, and applications[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1616-1637. [3]Goyal P, Ferrara E. Graph embedding techniques, applications, and performance: A survey[J]. Knowledge-Based Systems, 2018, 151: 78-94.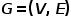 , where
, where 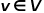 represents the node,
represents the node, 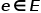 Represents an edge.
Represents an edge. 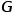 with node type mapping function
with node type mapping function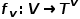 and edge type mapping function
and edge type mapping function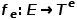 Associated.
Associated. 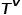 represents a collection of node types,
represents a collection of node types, 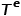 represents a collection of edge types.
represents a collection of edge types. 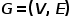 ,in
,in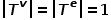 . That is to say, all nodes belong to one type and all edges belong to one type. For example, the user attention relationship graph in a social network has only one node type, user, and one edge type, attention relationship.
. That is to say, all nodes belong to one type and all edges belong to one type. For example, the user attention relationship graph in a social network has only one node type, user, and one edge type, attention relationship. 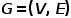 , where
, where 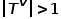 or
or 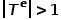 . That is to say, there is more than one node type or edge type. For example, in the graph structure in an academic network, there are multiple node types such as papers, authors, and conferences. The edge relationships include the creative relationship between authors and papers, papers and conferences. The publication relationship between them, the citation relationship between papers, etc.
. That is to say, there is more than one node type or edge type. For example, in the graph structure in an academic network, there are multiple node types such as papers, authors, and conferences. The edge relationships include the creative relationship between authors and papers, papers and conferences. The publication relationship between them, the citation relationship between papers, etc. 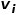 and node
and node 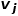 is expressed as
is expressed as 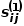 , there are
, there are 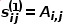 , where
, where 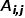 is the node # The weight of the edge
is the node # The weight of the edge 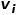 between
between 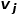 ## and node
## and node 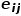 .
. 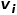 and node
and node 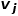
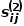 is the neighborhood of
is the neighborhood of 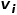
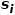 and # The similarity between
and # The similarity between 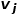 ##’s neighborhoods
##’s neighborhoods 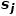 . As shown in Figure 1, because there is an edge connecting node f and node g, node f and node g are first-order similar. Although there is no edge connecting node e and node g, they have four identical neighbor nodes, so node e and node g are second-order similar.
. As shown in Figure 1, because there is an edge connecting node f and node g, node f and node g are first-order similar. Although there is no edge connecting node e and node g, they have four identical neighbor nodes, so node e and node g are second-order similar. 
 dimensional vectors to represent a graph, each vector represents An embedding of a part of a graph, such as a node or edge.
dimensional vectors to represent a graph, each vector represents An embedding of a part of a graph, such as a node or edge. 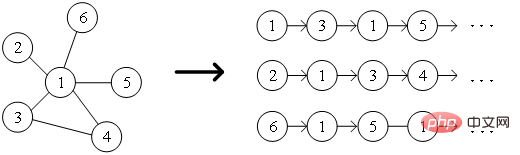
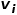 # in the graph, the word sequence corresponds to the node sequence obtained by a random walk, then for a random walk
# in the graph, the word sequence corresponds to the node sequence obtained by a random walk, then for a random walk 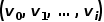 , define its optimization objective function as shown in the formula.
, define its optimization objective function as shown in the formula. 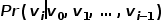
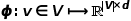 , to realize the mapping of nodes in the graph to
, to realize the mapping of nodes in the graph to 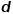 -dimensional vectors, then the problem is transformed into estimating the possibility of the following formula.
-dimensional vectors, then the problem is transformed into estimating the possibility of the following formula. 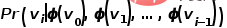
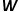 , and the other is the background word vector matrix
, and the other is the background word vector matrix  . These two weight matrices respectively represent the word vectors associated with words when they serve as different roles. Skip-gram is a model for predicting word context. It first learns the relationships between words from the corpus, and then uses these relationships to express the context of a specific word, that is, the vector representation of the word. That is to say, in the same sequence, the more frequently two words appear at the same time, the more similar the vector representations of the two words are. Apply this idea to the graph and define its optimization objective function as shown in the formula.
. These two weight matrices respectively represent the word vectors associated with words when they serve as different roles. Skip-gram is a model for predicting word context. It first learns the relationships between words from the corpus, and then uses these relationships to express the context of a specific word, that is, the vector representation of the word. That is to say, in the same sequence, the more frequently two words appear at the same time, the more similar the vector representations of the two words are. Apply this idea to the graph and define its optimization objective function as shown in the formula. 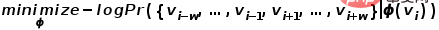
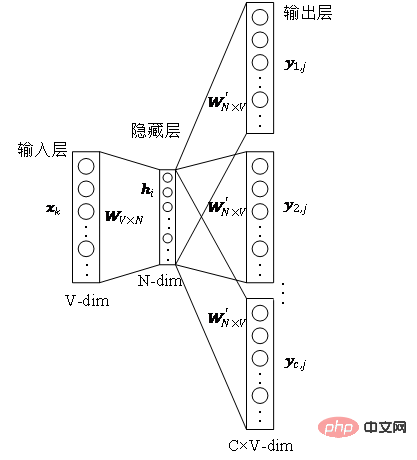
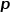 and parameters
and parameters 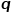 Guide whether each random walk tends to breadth-first sampling or depth-first sampling, so the adaptability is high. Assuming that node
Guide whether each random walk tends to breadth-first sampling or depth-first sampling, so the adaptability is high. Assuming that node 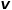 # is currently visited, the probability of next visiting node
# is currently visited, the probability of next visiting node 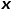 is as shown in the formula.
is as shown in the formula. 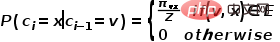
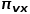
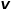 The transition probability to node
The transition probability to node 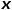 , where
, where 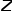 represents the normalization constant.
represents the normalization constant. 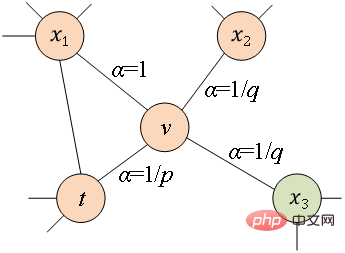
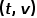 , and the next step is to visit node x, let
, and the next step is to visit node x, let 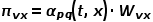 ,
, 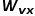 is the edge weight between nodes
is the edge weight between nodes 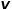 and
and 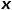 . In other words, when the graph is an unweighted graph,
. In other words, when the graph is an unweighted graph, 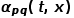 directly determines the transition probability of the node. When the graph is a weighted graph, the product of
directly determines the transition probability of the node. When the graph is a weighted graph, the product of 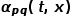 and the edge weight
and the edge weight 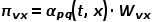 determines the final transition probability of the node .
determines the final transition probability of the node . 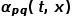 can be calculated according to the following formula, where
can be calculated according to the following formula, where 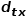 is the node
is the node 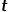 The shortest path distance between and node
The shortest path distance between and node 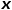 .
. 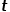 to node
to node 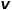 When you need to select the next hop node, there will be the following three situations.
When you need to select the next hop node, there will be the following three situations. 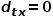 , return node
, return node 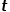 .
. 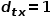 , select node
, select node 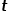 and node # Common adjacent nodes of
and node # Common adjacent nodes of 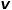 ##, such as node
##, such as node 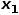 .
. 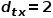 , select the node
, select the node 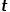 Adjacent nodes to unrelated nodes
Adjacent nodes to unrelated nodes 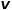 , such as nodes
, such as nodes 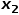 or
or 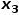 .
. 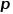 controls the probability of returning to the previous hop node, parameter
controls the probability of returning to the previous hop node, parameter 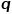 controls more whether to explore the local structure information or the global structure information of the network. The DeepWalk model is actually
controls more whether to explore the local structure information or the global structure information of the network. The DeepWalk model is actually 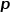 The Node2Vec model when the value of and
The Node2Vec model when the value of and 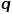 is set to 1.
is set to 1.
The above is the detailed content of A brief discussion on graph embedding algorithms. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- Technology trends to watch in 2023
- How Artificial Intelligence is Bringing New Everyday Work to Data Center Teams
- Can artificial intelligence or automation solve the problem of low energy efficiency in buildings?
- OpenAI co-founder interviewed by Huang Renxun: GPT-4's reasoning capabilities have not yet reached expectations
- Microsoft's Bing surpasses Google in search traffic thanks to OpenAI technology

