Use Python to implement automatic tracking of missiles, super burning!

Hello everyone, I am Brother J.

It is difficult to calculate this without some mathematical foundation. But it's different when we have computers. Relying on the extremely fast computing speed of computers, we can achieve it by using the idea of ​​​​differentiation and adding a little simple knowledge of trigonometry.

Okay, without further ado, let’s take a look at its algorithm principle and the picture:

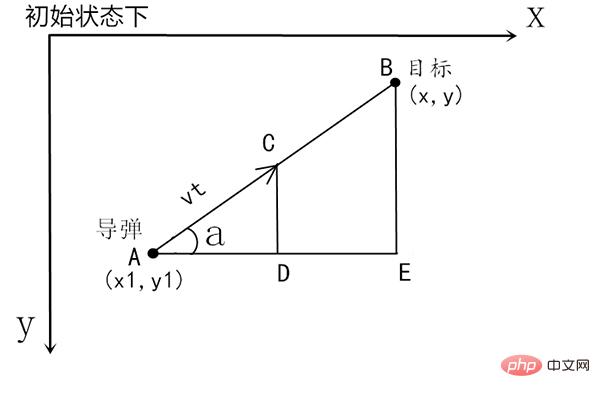
Since we will use pygame to demonstrate it later, its The coordinate system is with the y-axis pointing downward, so here we also use the coordinate system with the y-axis pointing downward.

The general idea of ​​the algorithm is to divide time t into small enough segments (such as 1/1000, the smaller the time slice is, the more accurate it is) based on the above figure. Each segment constructs the triangle as above to calculate the missile. The direction of walking in the next time slice (i.e. ∠a) and the distance traveled (i.e. vt=|AC|). At this time, the target moves again in the second time slice. At this time, the point C just calculated becomes The initial point of the second time slice, then construct a triangle at point C and the new target point on the second time slice to calculate a new vt, and then enter the third time slice, and repeat.

Assume that the initial coordinates of the missile and target are (x1, y1), (x, y) respectively, and construct a right triangle ABE. This triangle is used to find the sine and cosine values ​​​​of ∠a, because vt It is set by ourselves. We need to calculate how much the x and y coordinates of point A have moved respectively. The value of the movement is the length of AD and CD. These two can be multiplied by vt cos(a) and sin(a) respectively.

Calculate sin(a) and cos(a), sine versus slope, cosine adjacent versus slope, the hypotenuse can be calculated using the two-point distance formula, that is:

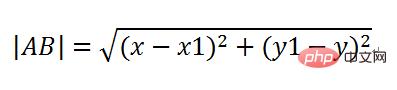
So

The length of AC is the speed of the missile multiplied by time, which is |AC|=vt, and then the lengths of AD and CD can be calculated, so this After a time slice has passed, the missile should appear at the new position point C, and its coordinates are the x plus AD and y minus CD of the old point A.

So, the new coordinates of point C are:

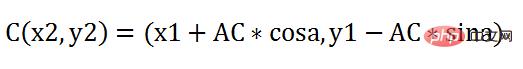
Just keep repeating this operation repeatedly. Well, in order to be more vivid, put the first Take a look at the first time slice and the second time slice together:

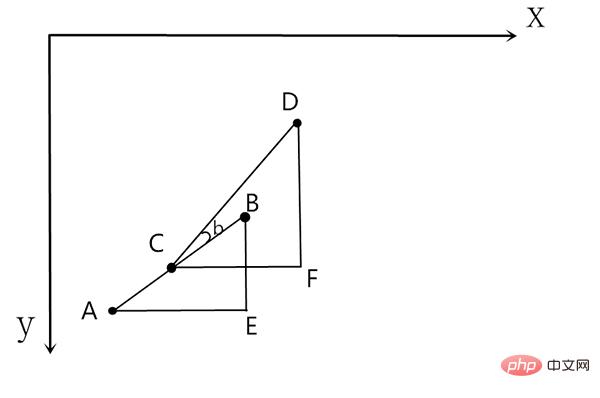
The first one is the triangle constructed by the time slice is ABE. After a time slice, the target From point B to point D, the missile is now at point C, so we construct a new triangle CDF and repeat the calculation process just now. The angle ∠b in the picture is the angle at which the missile needs to rotate. In reality, it only takes each time Just correct the direction of the missile with a piece of film. How to change the direction of the missile is not a problem we need to study.

Okay, since I have been using Python's pygame library to make a small game recently, we will next Use pygame to demonstrate this effect. The effect is as follows:

The very simple code is as follows:

import pygame,sys
from math import *
pygame.init()
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/red_pointer.png').convert_alpha()
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
old_angle=0
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点线段的弧度值
x1,y1=(x1+section*cosa,y1-section*sina)
d_angle = degrees(angle)#弧度转角度
screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
dis_angle=d_angle-old_angle#dis_angle就是到下一个位置需要改变的角度
old_angle=d_angle#更新初始角度
pygame.display.update()

If the missile is only considered as a particle, Then the above algorithm is enough. I did not do the rotation of the missile, because a particle does not need to be rotated whether it is head or tail. Of course, this premise is that when the missile image you load is very small, it does not look like a problem if it does not rotate. But doing rotation in pygame is not an easy task. Let’s first replace the picture with a rectangle, and then add the rotation function to see the effect

missiled = pygame.transform.rotate(missile, -(d_angle))
screen.blit(missiled, (x1-missile.get_width(), y1-
missile.get_height()/2))

because of the picture The coordinate point is the point in its upper left corner, so if we want the coordinates of the picture to be fixed at the tip of the arrow, then just reduce the actual printing position x of the picture by reducing the length of the picture and y by reducing the width by half. But the actual running effect is not good:

大致方向相同，但是图片箭头的尖点并没有一直跟随鼠标，这是为什么呢。经过一番研究，我发现原来是这个图旋转的机制问题，我们看看旋转后的图片变成什么样了：

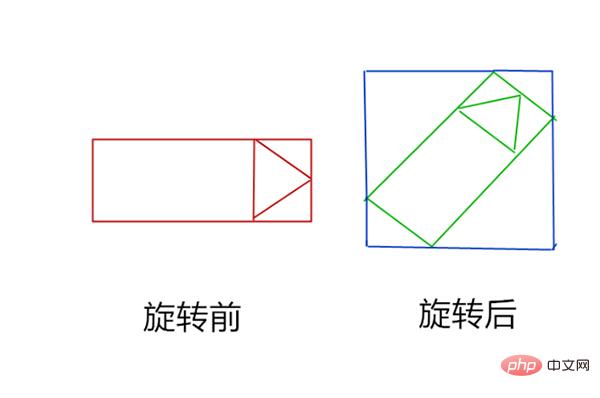
旋转后的图片变成了蓝色的那个范围，根据旋转角度的不同，所变成的图片大小也不一样，我们看旋转90的情况

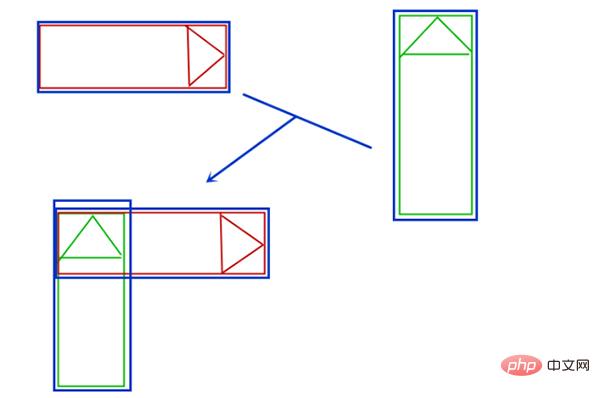
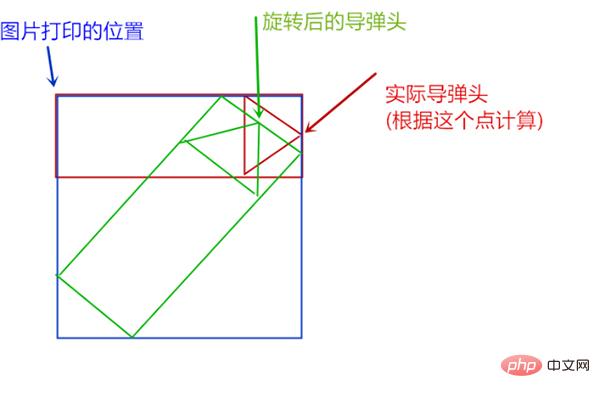
我们发现，旋转后的图片不仅面积变大了，导弹头的位置也变了。那应该怎么解决这个问题呢？思路是，每一次旋转图片以后，求出旋转图的头位置（图中的绿色箭头点），然后把绿图的打印位置移动一下，下，x，y分别移动两个头的距离，就可以让旋转后的导弹头对准实际我们参与运算的那个导弹头的位置，移动后应该是这样的：

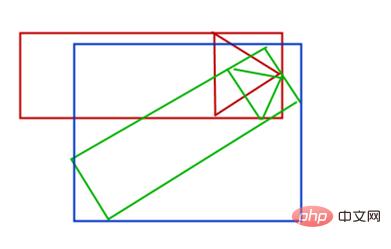
这样，两个导弹头的点就一致了。接下来我们分析求旋转后的导弹头的算法。根据旋转角度的不同，旋转角在不同象限参数不一样，所以我们分为这四种情况

1，2象限

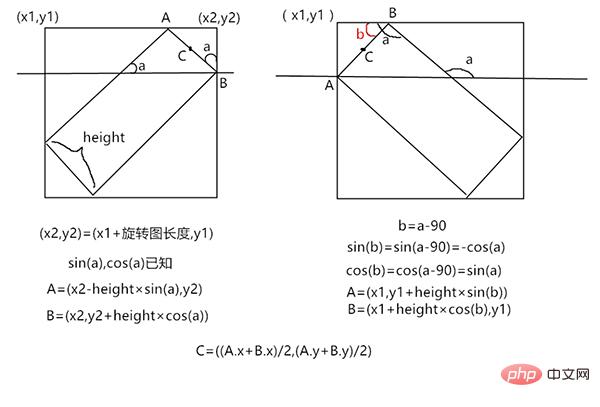
3，4象限，它的旋转只有正负0—180，所以3，4象限就是负角

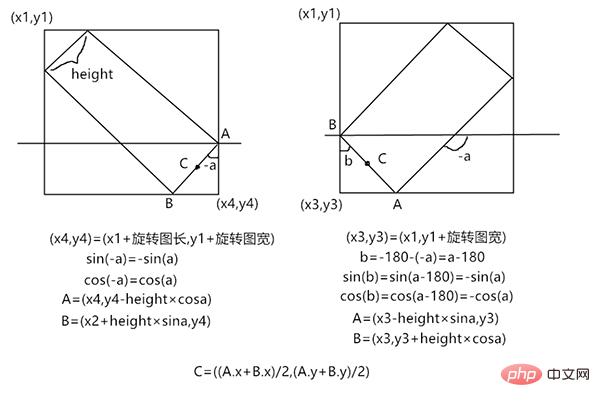
显示图片的时候我们将他移动

screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))

这里的 (x1-width, y1-height/2) 其实才是上图中的 (x1, y1)  

所以最后我们加入相关算法代码，效果就比较完美了

大功告成，最后附上全部的算法代码

import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点间线段的弧度值
fangle=degrees(angle) #弧度转角度
x1,y1=(x1+section*cosa,y1-section*sina)
missiled=pygame.transform.rotate(missile,-(fangle))
if 0<=-fangle<=90:
A=(width*cosa+x1-width,y1-height/2)
B=(A[0]+height*sina,A[1]+height*cosa)
if 90<-fangle<=180:
A = (x1 - width, y1 - height/2+height*(-cosa))
B = (x1 - width+height*sina, y1 - height/2)
if -90<=-fangle<0:
A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
if -180<-fangle<-90:
A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
B = (x1 - width,A[1]+height*cosa )
C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
screen.fill((0,0,0))
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
screen.blit(textc, (x,y)) #鼠标用一个红色*代替
pygame.display.update()

以上便是用Python模拟导弹自动追踪的代码实例。

The above is the detailed content of Use Python to implement automatic tracking of missiles, super burning!. For more information, please follow other related articles on the PHP Chinese website!