The graph neural network was published in a Nature sub-journal, but it was revealed that it was 104 times slower than the ordinary algorithm. Questioners: Is it a new height?

GNN is a very popular field in recent years. Recently, a Nature sub-journal paper proposed a method to use GNN to solve combinatorial optimization problems, and claimed that the performance of the GNN optimizer is equivalent to or even exceeds existing solvers. However, this paper has attracted some doubts: some people pointed out that the performance of this GNN is actually not as good as the classic greedy algorithm, and the speed is much slower than the greedy algorithm (for problems with one million variables, the greedy algorithm is better than the GNN 104 times faster). So the skeptics said, "We don't see any good reason to use these GNNs to solve this problem, it's like using a sledgehammer to crack nuts." They hope that the authors of these papers can first solve the difficult problem before claiming the superiority of the method. Compare the benchmarks.

In recent years, neural networks have solved many difficult problems in application and basic science, including discrete combinatorial optimization problems, which are also the basis for our understanding of the limits of computing.

Martin JA Schuetz et al.’s 2022 study "Combinatorial optimization with physics-inspired graph neural networks" [4] proposed to use physics-inspired unsupervised graph neural networks (GNN) to This approach seems promising for solving combinatorial optimization problems on graphs and has been published in a high-impact journal (Nature Machine Intelligence). The study tested the performance of GNNs on two standard optimization problems: max-cut and maximal independent set (MIS). This newly proposed GNN optimizer has a very nice property: it can be extended to many larger instance problems.

Paper address: https://arxiv.org/pdf/2107.01188.pdf

However, a recent new paper "Cracking nuts with a sledgehammer: when modern graph neural networks do worse than classical greedy algorithms" has questioned the research of Martin JA Schuetz et al., believing that Martin JA Schuetz et al. The GNN optimizer is "cracking nuts with a sledgehammer, similar to hitting mosquitoes with a mortar", which wastes resources and has poor results.

##Paper address: https://arxiv.org/abs/2206.13211

The MIS problem is defined as follows: Given an undirected random regular graph (d-RRG) with n nodes and degree fixed to d, the independent set (IS) refers to the subset of vertices that does not contain any nearest neighbor pairs. ; The MIS problem requires finding the largest IS, whose size is called α. MIS is an NP-hard problem, but one would like to find an algorithm to find an IS with a size as close as possible to the maximum in polynomial time. Furthermore, a good algorithm should not suffer performance degradation for larger values ​​of n.

The new GNN proposed by Martin JA Schuetz et al. can find IS for very large graphs (n≤ 10^6): the algorithm running time is proportional to the problem size: t∼ n^ 1.7, and the algorithm performance remains stable as n increases, as shown in Figure 1 below.

​

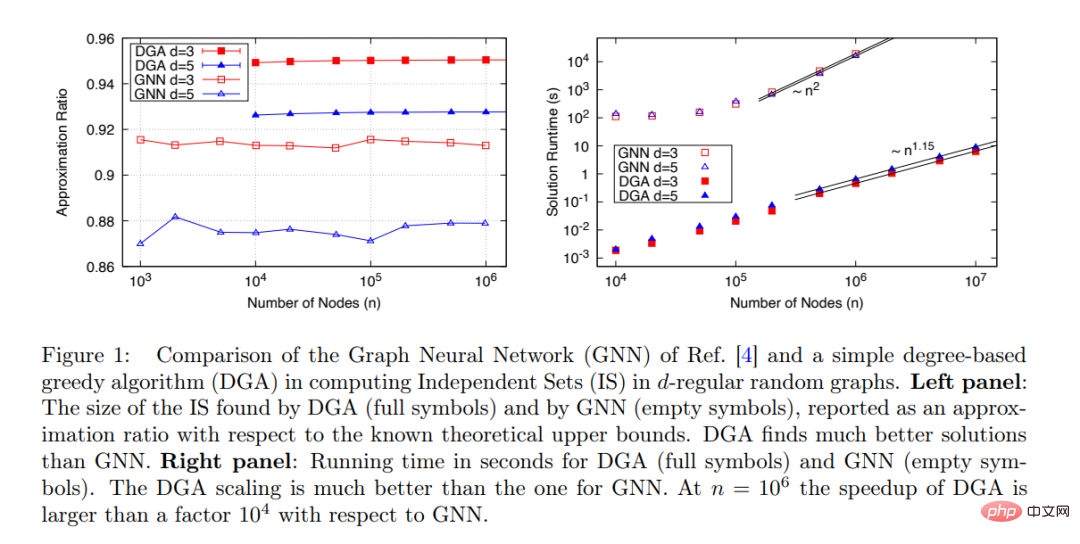
However, when comparing the performance of the proposed GNN with other available algorithms, this study only compares with Boppana- Halldorsson (BH) approximation algorithm [8] has been compared. When n≤500, this algorithm has a running time of t∼n^2.9. ​

There are actually many other algorithms for calculating IS that are much faster than BH, and the study should compare the proposed GNN optimizer with these algorithms. Among them, the simplest algorithm is the greedy algorithm (GA) [9]. After the degree-based greedy algorithm (DGA) is optimized, the running time is almost linear with the number of nodes n. ​

This study compares the GNN optimizer (open) and DGA (solid) proposed by Martin JA Schuetz et al. to find MIS on d-RRG with d=3 and d=5 performance. As shown in Figure 1 (right), from the perspective of the relationship between running time and problem size (number of nodes), DGA is much better than GNN. The running time of the former is almost proportional to the number of nodes n. There is a linear relationship (the exponent is 1.15 probably due to pre-asymptotic effects), while the running time of GNN has an almost quadratic relationship with the number of nodes n.

This study believes that Martin JA Schuetz et al.’s claim that "the performance of optimizers based on graph neural networks is equivalent to or better than existing solvers, and has the ability to surpass the current SOTA model. "Can be extended to problems with millions of variables" cannot withstand scrutiny and is inconsistent with actual experimental results. Martin JA Schuetz and others should revise the paper. ​

This study clarifies the performance of DGA in detail and believes that this simple greedy algorithm should be regarded as a minimum benchmark, and the performance of any new algorithm must be at least better than that of DGA Good talents are adopted.

Of course, DGA is just an extremely simple algorithm, and there are many other standard algorithms that are better than DGA. Maria Chiara et al.'s 2019 paper "Monte carlo algorithms are very effective in finding the largest independent set in sparse random graphs" provides an in-depth study of the performance of multiple algorithms for solving MIS problems. ​

##Based on this, this study raises a question: "When evaluating a new optimization algorithm, what really difficult problems should be used as a benchmark to test the performance of the algorithm?"

For example, this study considers MIS on the d-RRG of d16. The results for d=20 and d=100 can be compared here to the results given in the 2019 paper "Monte carlo algorithms are very effective in finding the largest independent set in sparse random graphs".

Obviously, a good optimization algorithm should be completed in n polynomial time. It would be better if the relationship is linear. The quality of the solution found should be better than the simple existing algorithm. , and the quality should not decline as n increases.

The study concluded: Currently, neural network-based optimizers (such as the optimizer proposed by Martin JA Schuetz et al.) do not meet the above requirements and cannot compete with simple standard algorithms to solve difficult optimization problems. It is crucial to explore whether neural networks can meet this requirement, or whether there are deeper reasons for their failure.

The above is the detailed content of The graph neural network was published in a Nature sub-journal, but it was revealed that it was 104 times slower than the ordinary algorithm. Questioners: Is it a new height?. For more information, please follow other related articles on the PHP Chinese website!