Is the mathematics behind the diffusion model too difficult to digest? Google makes it clear with a unified perspective

In recent times, AI painting has been very popular.

While you marvel at AI’s painting capabilities, what you may not know is that the diffusion model plays a big role in it. Take the popular model OpenAI's DALL·E 2 as an example. Just enter a simple text (prompt) and it can generate multiple 1024*1024 high-definition images.

Not long after DALL·E 2 was announced, Google subsequently released Imagen, a text-to-image AI model that can generate realistic images of the scene from a given text description. Image.

Just a few days ago, Stability.Ai publicly released the latest version of the text generation image model Stable Diffusion, and the images it generated reached commercial grade.

Since Google released DDPM in 2020, the diffusion model has gradually become a new hot spot in the field of generation. Later, OpenAI launched GLIDE, ADM-G models, etc., which made the diffusion model popular.

Many researchers believe that the text image generation model based on the diffusion model not only has a small number of parameters, but also generates higher quality images, and has the potential to replace GAN.

However, the mathematical formula behind the diffusion model has discouraged many researchers. Many researchers believe that it is much more difficult to understand than VAE and GAN.

Recently, researchers from Google Research wrote "Understanding Diffusion Models: A Unified Perspective". This article shows the mathematical principles behind the diffusion model in extremely detailed ways, with the purpose of letting others Researchers can follow along and learn what diffusion models are and how they work.

Paper address: https://arxiv.org/pdf/2208.11970.pdf As for how "mathematical" this paper is, the author of the paper describes it like this : We demonstrate the mathematics behind these models in excruciating detail.

The paper is divided into 6 parts, mainly including generative models; ELBO, VAE and hierarchical VAE; variational diffusion models; score-based generative models, etc.

The following is an excerpt from the paper for introduction:

Generation model​

Given an observation sample x in the distribution, the goal of the generative model is to learn to model its true data distribution p(x). After the model is learned, we can generate new samples. Additionally, in some forms, we can also use learning models to evaluate observations or sample data.

There are several important directions in the current research literature. This article only briefly introduces them at a high level, mainly including: GAN, which models the sampling process of complex distributions. Learn adversarially. Generative models, which we can also call "likelihood-based" methods, can assign high likelihood to observed data samples and usually include autoregression, normalized flow, and VAE. Energy-based modeling, in this approach, the distribution is learned as an arbitrary flexible energy function and then normalized. In score-based generative models, instead of learning to model the energy function itself, the score based on the energy model is learned as a neural network. ​

In this study, this paper explores and reviews diffusion models, as shown in the paper, they have likelihood-based and score-based interpretations.

Variational Diffusion Model​

Looking at it in a simple way, a Variational Diffusion Model (VDM) can be considered as having three main Restricted (or assumed) Markov hierarchical variational autoencoders (MHVAE), they are:

• The latent dimension is exactly the same as the data dimension;
• The structure of the latent encoder at each time step is not learned, it is predefined as linear Gaussian model. In other words, it is a Gaussian distribution centered on the output of the previous time step;
• #The Gaussian parameters of the potential encoder change over time, and the potential distribution standard at the final time step T in the process is Gaussian distribution.

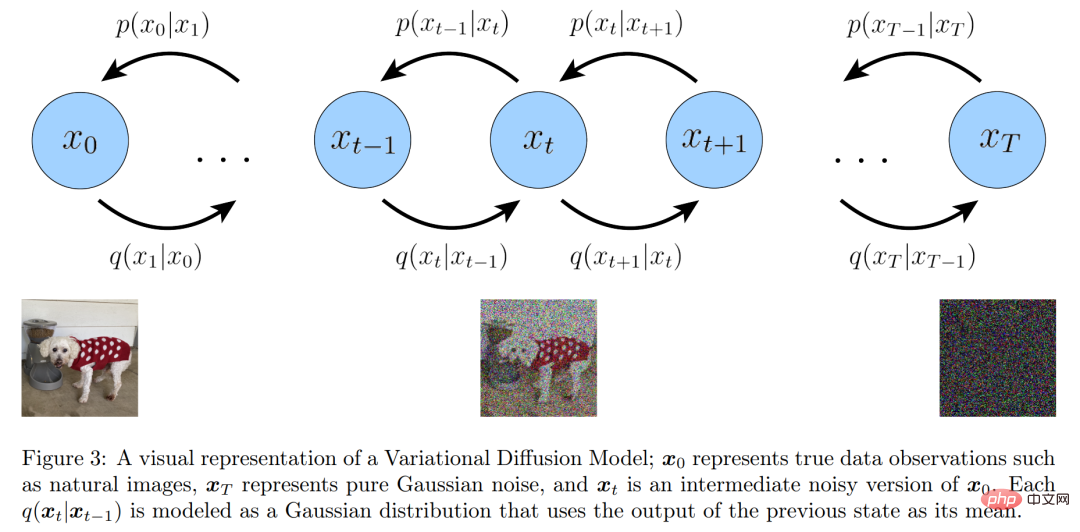
Visual representation of the variational diffusion model

Additionally, we explicitly maintain Markov properties between hierarchical transformations from standard Markov hierarchical variational autoencoders. They expanded the implications of the above three main assumptions one by one.

Starting from the first assumption, due to misuse of symbols, real data samples and latent variables can now be represented as x_t, where t=0 represents real sample data, t ∈ [1 , T] represents the corresponding latent variable, and its hierarchical structure is indexed by t. The VDM posterior is the same as the MHVAE posterior, but can now be rewritten as follows:

From the second hypothesis, It is known that the distribution of each latent variable in the encoder is a Gaussian distribution centered on the previously stratified latent variable. Different from MHVAE, the structure of the encoder at each time step is not learned, it is fixed as a linear Gaussian model, where the mean and standard deviation can be preset as hyperparameters or learned as parameters. Mathematically, the encoder transformation is expressed as follows:

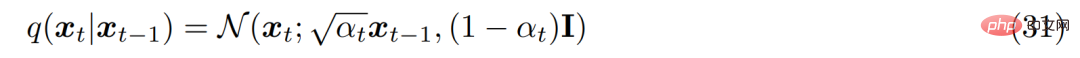
For the third hypothesis, α_t is fixed or learnable according to The obtained schedule evolves over time, so that the distribution of the final latent variable p(x_T) is a standard Gaussian distribution. Then the joint distribution of MHVAE can be updated, and the joint distribution of VDM can be written as follows:

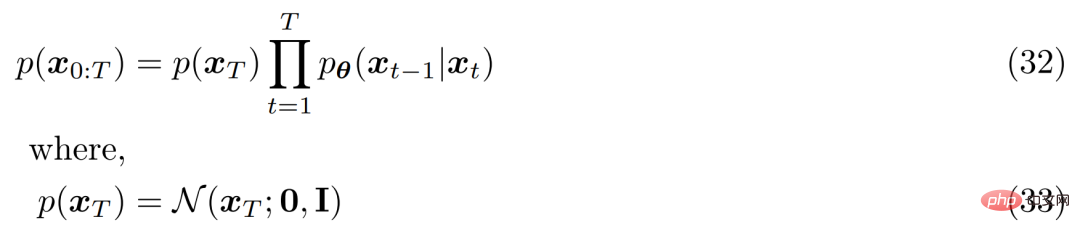
In general, this A series of assumptions describe the stable noise of an image as it evolves over time. The researchers progressively corrupted the image by adding Gaussian noise until it eventually became identical to Gaussian noise.

Similar to any HVACE, VDM can be optimized by maximizing the Evidence Lower Bound (ELBO), which can be derived as follows:

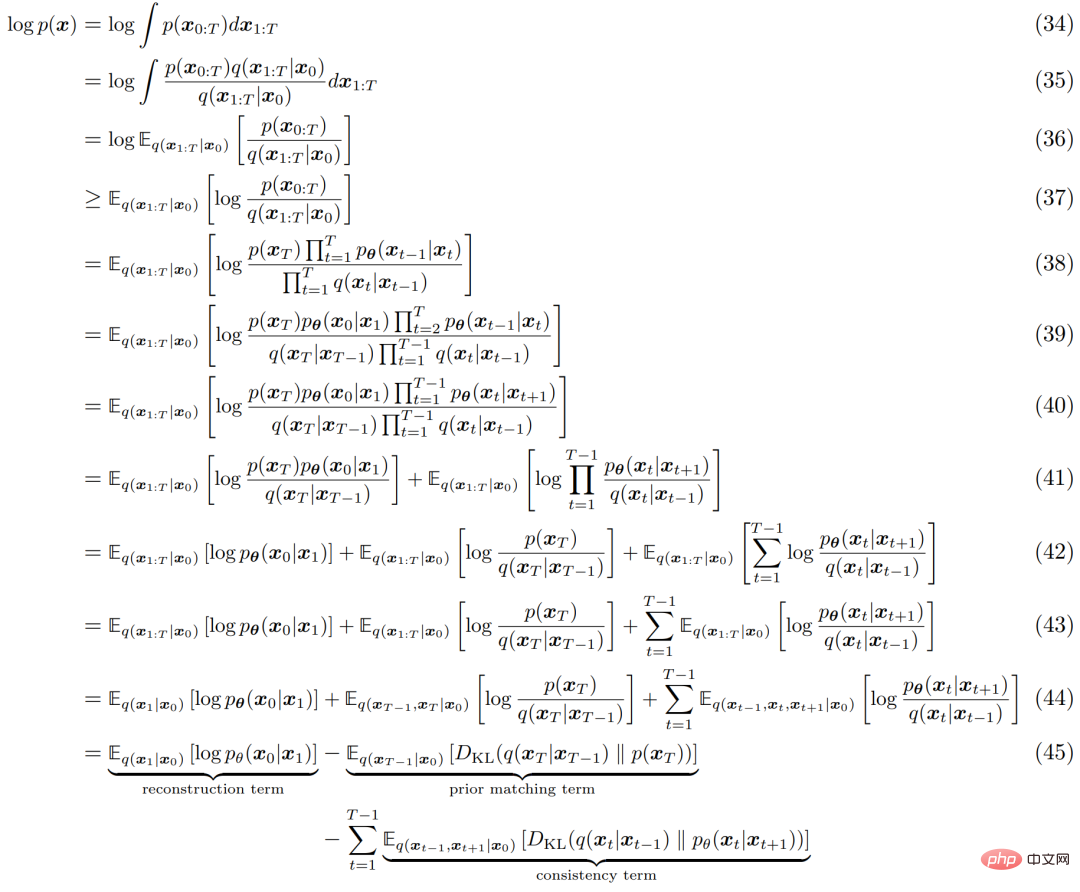
The explanation process of ELBO is shown in Figure 4 below:

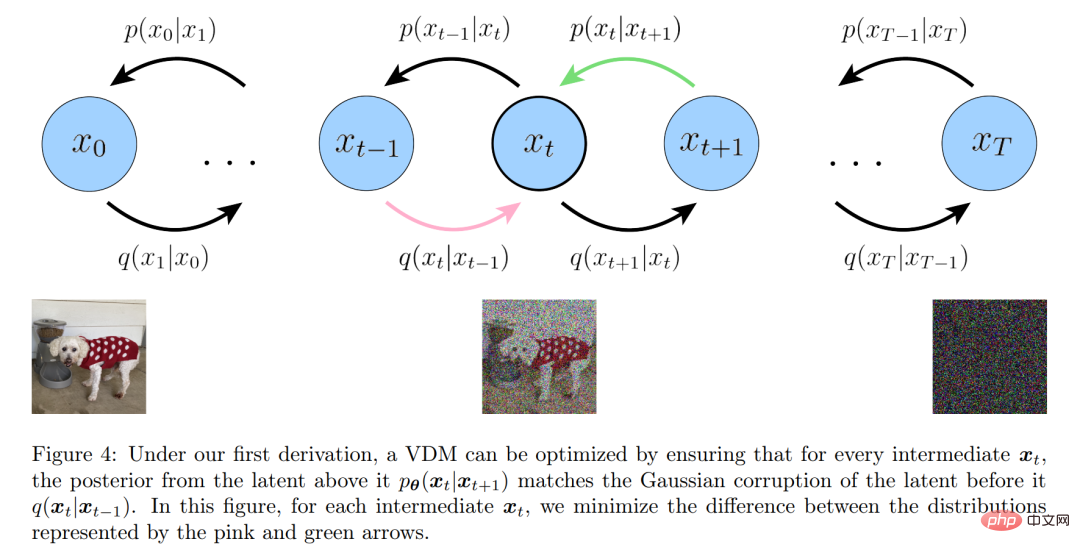
Three equivalent explanations

As demonstrated before, a variational diffusion model can be trained simply by learning a neural network to predict the original x_t from an arbitrary noisy version x_t and its time index t Natural image x_0. However, there are two equivalent parameterizations of x_0, allowing two further interpretations of the VDM to be developed.

First, you can use the heavy parameterization technique. When deriving the form of q(x_t|x_0), Equation 69 can be rearranged as follows:

Bring it into the previously derived true denoising transformation mean µ_q(x_t, x_0), you can re-derive it as follows: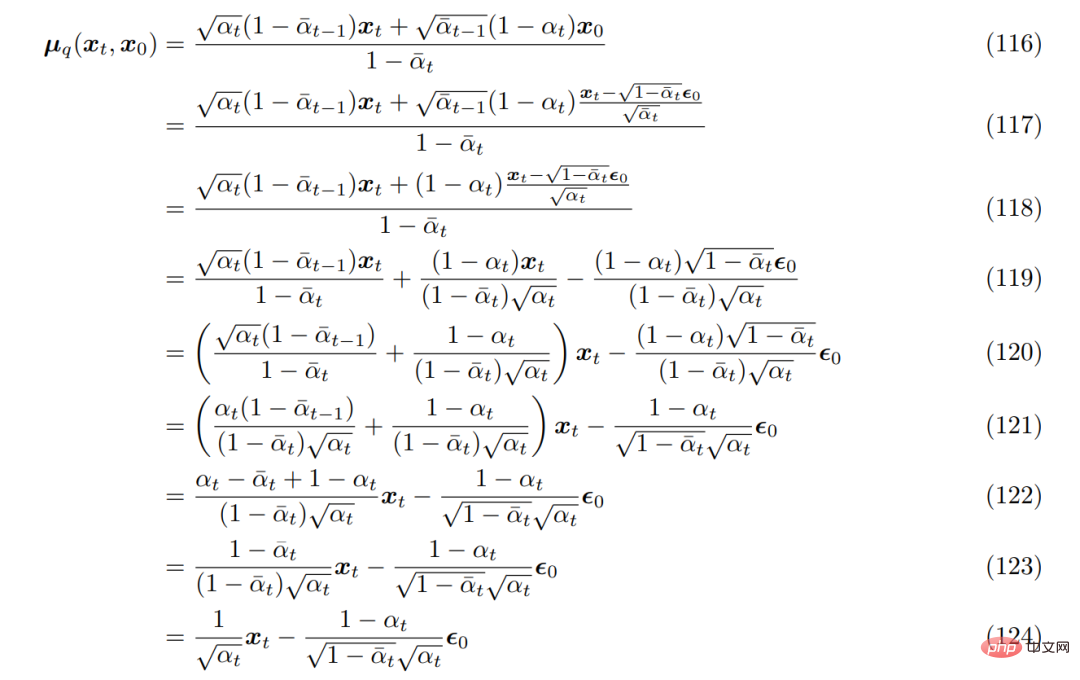

So you can The approximate denoising transformed mean µ_θ(x_t, t) is set as follows:

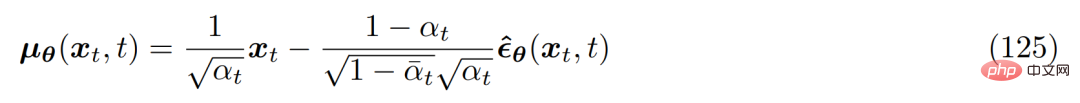
and the corresponding optimization problem becomes as follows :

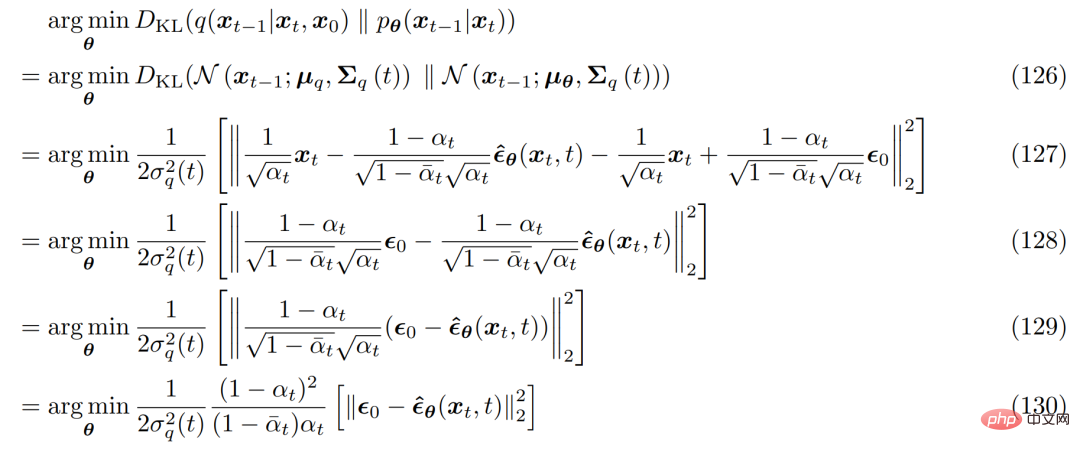
In order to derive the three common interpretations of variational diffusion models, one needs to turn to the Tweedie formula, which refers to is that when a sample is given, the true mean of an exponential family distribution can be estimated by the maximum likelihood estimate of the sample (also called the empirical mean) plus some correction term involving the estimated score.

Mathematically speaking, for a Gaussian variable z ∼ N (z; µ_z, Σ_z), the Tweedie formula is expressed as follows:

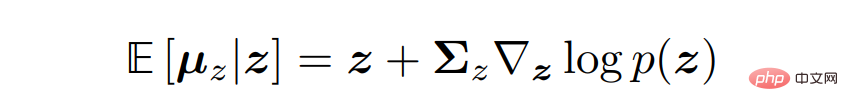
Score-based generative model

Researchers have shown that variational diffusion models can be learned simply by optimizing a neural network s_θ(x_t, t) is obtained to predict a score function ∇ log p(x_t). However, the scoring term in the derivation comes from the application of Tweedie's formula. This does not necessarily provide good intuition or insight into what exactly the score function is or why it is worth modeling. ​

Fortunately, this intuition can be obtained with the help of another type of generative model, namely the score-based generative model. The researchers indeed demonstrated that the previously derived VDM formulation has an equivalent fraction-based generative modeling formulation, allowing flexible switching between the two interpretations. ​

To understand why optimizing a score function makes sense, the researchers revisited energy-based models. An arbitrary flexible probability distribution can be written as follows:

A way to avoid calculating or modeling normalization constants The method is to use the neural network s_θ(x) to learn the score function ∇ log p(x) of the distribution p(x). It is observed that both sides of Equation 152 can be logarithmically differentiated:

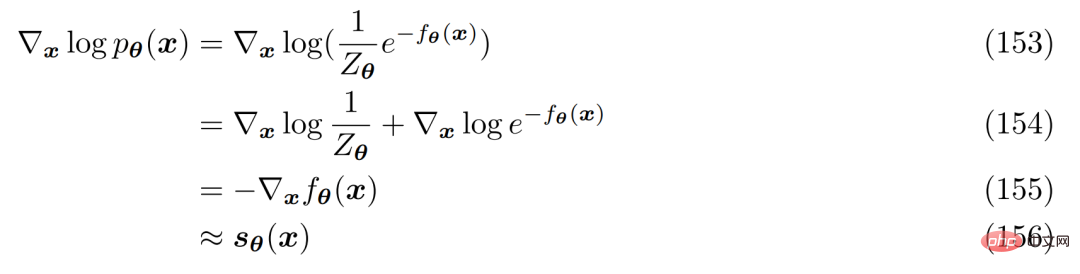
which can be freely expressed as a neural network , does not involve any normalization constants. The score function can be optimized by minimizing the Fisher divergence using the true score function. ​

Intuitively speaking, the score function defines a vector field over the entire space where the data x is located, and points to The model is shown in Figure 6 below.

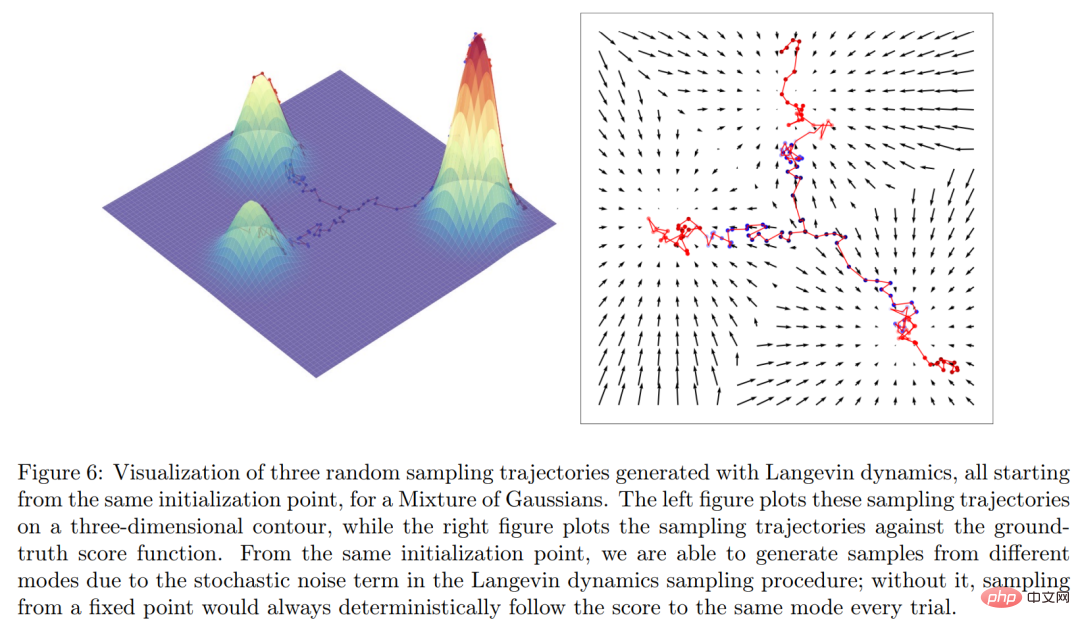
Finally, the researchers established a variational diffusion model and a score-based Generate explicit relationships between models.

Please refer to the original paper for more details.

The above is the detailed content of Is the mathematics behind the diffusion model too difficult to digest? Google makes it clear with a unified perspective. For more information, please follow other related articles on the PHP Chinese website!