How to prove that a problem is a VPN problem? Computer scientists have found a simple way

The P/NP problem is an unsolved problem in the field of computational complexity. People have been trying to find an answer to a question: "Can we efficiently solve all computing problems in a reasonable time?"

What is a reasonable time? In fact, problems that can be solved before the end of the universe are considered within a reasonable time. Yet many problems appear to be difficult to solve in a reasonable time, requiring mathematics to demonstrate the difficulty of these problems.

A 2021 study answers the above question, which confirms: A large proportion of problems are difficult to effectively solve.

Paul Beame of the University of Washington commented on this research: "Just like climbing a mountain, this research is a foothold on the road to computational theory research."

The three researchers of the study: computer scientists Srikanth Srinivasan (left), Nutan Limaye (upper right) and Sébastien Tavenas.

The study considered problems involving only addition and multiplication, but these problems become very difficult when they are restricted to solving in a specific way (a certain alternating pattern of addition and multiplication).

Surprisingly, the study did not use a new framework or tool. Instead, the authors managed to bypass a decades-long collaboration between Wigderson, a professor in the School of Mathematics at the Institute for Advanced Study, and Noam Nisan of the Hebrew University of Jerusalem. Mathematics barriers described in the work.

One of the researchers, Srikanth Srinivasan of Aarhus University in Denmark, said: "We realized that there is a very simple way to get around this obstacle. And if we can do it in such a simple way, If you think something is impossible, you can definitely find a better way."

Important Question

After the advent of computers, scientists discovered that computer algorithms can solve many problems, but sometimes these algorithms cost takes too long - longer than the actual calculation time.

They began to suspect that some problems were inherently too difficult to solve, no matter how large or small they were. For example, in graphs, an important problem is to determine whether there is a Hamiltonian path, that is, there is a path that passes through each vertex exactly once. Increasing the number of vertices (and edges) should take longer to determine whether such a path exists, but even the best algorithms take exponentially longer time as the graph size increases, making solving this The problem becomes unrealistic.

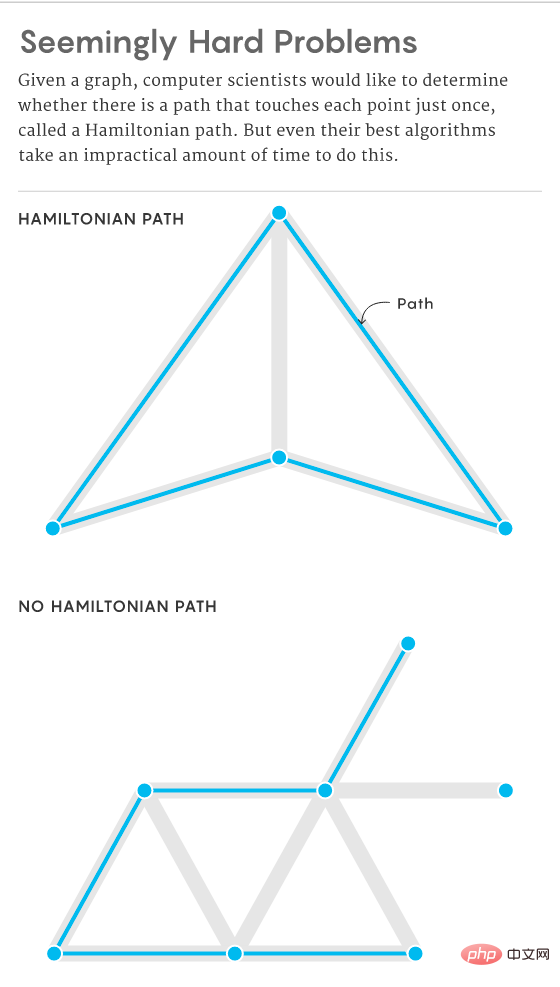
Computer scientists try to prove that any algorithm that is effective in some way to solve one difficult problem in a certain class of problems can be translated into a solution to other similarly difficult problems. They call this type of problem NP problem.

Of course, there are many problems that don’t seem difficult and don’t take too much time to solve. Many of these problems are also equivalent in some sense, and such problems are called P problems. They argue that NP problems are indeed more difficult than P problems and that NP problems can never be solved efficiently. But without evidence, this idea may be wrong.

So computer scientists began looking for ways to prove that NP problems are indeed harder. This required showing that NP problems must take exponential time to solve, but proving this was not easy.

How difficult is "hard"?

Imagine a specific set of problems that require only addition and multiplication. For example, given a set of points, it is possible to compute all possible Hamiltonian paths (if they exist) using the data about the points, just by addition and multiplication.

As the problem size increases, some arithmetic problems (such as calculating Hamiltonian paths) take more time. In 1979, Leslie Valiant of Harvard University showed that many arithmetic problems are equivalent in terms of difficulty, while others are equivalent in terms of no difficulty. Computer scientists later named these two types of problems—VNP and VP, respectively—after him.

Like P and NP problems, we cannot prove the difficulty of the VNP problem. We only know that the VNP problem is more difficult than the NP problem because it is based on the latter. For example, to calculate the path, you first need to determine the path. does it exist.

"It's harder than NP, so it should be easier to show that it's hard," Shpilka said.

In the following decades, computer scientists made much greater progress on the VP vs. VNP problem than they did on the P vs. NP problem, but most of it was limited to the algebra known as Valiant's creation. subfields of complexity. Before the recent work of Limaye, Srinivasan, and Tavenas, it was still difficult to tell whether there were problems with arithmetic in the general sense.

Adjusting Polynomials

This new work helps explore the way computer scientists think about addition and multiplication problems. Mathematically, these problems can be written in terms of polynomials (e.g. x^2 5y 6), which are composed of variables that are added and multiplied.

For any particular problem, such as computing a Hamiltonian path, you can construct a polynomial that represents it. For example you could use a variable to represent each point and edge, so that as more points and edges are added, more variables can be added to the polynomial.

To show that an arithmetic problem like computing a Hamiltonian path is difficult, one needs to show that as more points and edges are added, the corresponding polynomials require more operations to be solved in exponential time. For example, x^2 requires one operation (x * x), while x^2 y requires two operations (x * x plus y). The number of operations is called the size of the polynomial.

But the size of the polynomial is difficult to determine. For example the polynomial x^2 2x 1. It seems to have magnitude 4 (two multiplications and two additions), but the polynomial can be rewritten as the product of two sums, (x 1)(x 1), which has fewer operands - two additions, One multiplication. Often, as a problem grows in size and more variables are added to the polynomial, mathematical transformations can help simplify and reduce its size.

A few years after Valiant's research, computer scientists found a way to make the size of the problem easier to analyze. To do this, they proposed a property called "depth", which specifies the number of times the polynomial switches or alternates between sums and products. For example, the polynomial x^2 2x 1 has depth 2 because it is the sum of products (like x^2 and 2x). In contrast, the expression (x 1)(x 1) has a depth of 3 because it has the same depth as 0 (x 1)(x 1) as a sum of products.

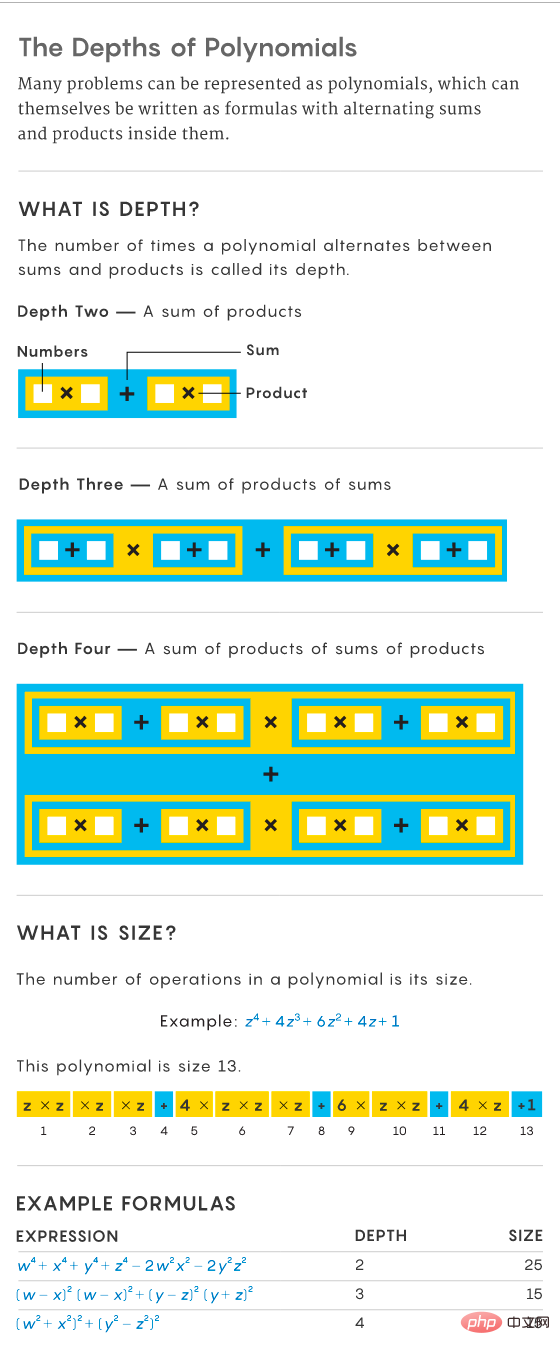
To simplify polynomials, computer scientists constrain them to a fixed form with a property called "constant depth," in which the pattern of sums and products does not change over time. changes as the problem grows. This makes them more fixed in size, with the size of the polynomial decreasing as its depth increases. An expression for some constant depth is called a formula. Constant depth allows more progress in the study of polynomials.

Magical "Depth"

In 1996, a paper by Nisan and Wigderson focused on solving the problem of matrix multiplication. They simplified this problem in two ways. First, they expressed it using the formula for constant depth - a depth of 3. Second, they only considered formulas with some simple structure in which each variable has a maximum exponent of 1, which makes the original problem a "multilinear" problem.

Computer scientists have discovered that certain problems can be converted into relatively simple set-multilinear structures at the expense of a sub-exponential increase in the size of the polynomial (comparable to the growth rate of exponential growth).

Nisan and Wigderson subsequently showed that the matrix multiplication problem takes exponential time to solve as the matrix grows larger. In other words, they show that an important problem is hard, and they make an effort to show that a class of problems is hard. However, their results only hold for formulations with simple, collective multilinear structures.

Leslie Valiant

Increasing the depth of a polynomial will often cause its size to decrease. Over time, computer scientists have made the trade-off between these two properties more precise. They show that adding two depth levels to depth 3, ensemble multilinear polynomials can balance the size gain of their ensemble multilinear structure. If structured formulas at depth 5 take exponential time, so do depth 3 formulas of a general, unstructured nature.

New work by Srikanth Srinivasan et al. shows that deep 5-set multilinear formulations of matrix multiplication problems do indeed grow at an exponential rate. This means that the general depth 3 formula also takes exponential time. They then showed that a similar pattern holds for all depths (not just 3 and 5). With this relationship, they showed that the size of a general formula of any depth for the same problem grows exponentially with the size of the problem.

They also show that it is difficult to express matrix multiplication in a formula with constant depth, no matter what the depth is.

The results of this study provide the first general understanding of when an arithmetic problem is "hard" - when it cannot be expressed in a constant-depth formula. The specific problem of matrix multiplication is known as the VP problem. And it is known that the VP problem is relatively easy when it is not restricted to constant depth, so it turns out that constant depth is the source of the "difficulty" of the problem.

Are VNP problems harder than VP problems? The new results don't show this directly, they only show that the constant depth formula is hard. But this is still an important milestone in proving that the VNP problem cannot be equivalent to the VP problem.

For the larger P vs. NP problem, we can now be more optimistic that the answer will one day be found. After all, in order to solve difficult problems, we first need to know which directions are hopeless.

The above is the detailed content of How to prove that a problem is a VPN problem? Computer scientists have found a simple way. For more information, please follow other related articles on the PHP Chinese website!