Towards Verifiable AI: Five Challenges of Formal Methods

Artificial intelligence is a computing system that attempts to imitate human intelligence, including some human functions that are intuitively related to intelligence, such as learning, problem solving, and rational thinking and action. Broadly interpreted, the term AI covers many closely related fields such as machine learning. Systems that make heavy use of AI are having significant social impacts in areas such as healthcare, transportation, finance, social networks, e-commerce, and education.

This growing social impact has also brought with it a series of risks and concerns, including errors in artificial intelligence software, cyberattacks and artificial intelligence system security. Therefore, the issue of verification of AI systems, and the broader topic of trustworthy AI, has begun to attract attention from the research community. “Verifiable AI” has been established as a goal for designing AI systems, a verifiable AI system with strong and ideally provable correctness guarantees on specific mathematical requirements. How can we achieve this goal?

Recently, a review article in "The Communications of ACM" tried to think about the challenges facing verifiable AI from the perspective of formal verification, and gave some principled solutions. . The authors are Professors S. Shankar Sastry and Sanjit A. Seshia, Chair of the Department of Electrical Engineering and Computer Science at UC Berkeley, and Dorsa Sadigh, Assistant Professor of Computer Science at Stanford University.

In computer science and engineering, formal methods involve the rigorous mathematical specification, design, and verification of systems. At its core, formal methods are about proof: formulating specifications that form the obligations of proof, designing systems to fulfill these obligations, and verifying through algorithmic proof searches that the system indeed conforms to its specifications. From specification-driven testing and simulation to model checking and theorem proving, a range of formal methods are commonly used in computer-aided design of integrated circuits and have been widely used to find bugs in software, analyze cyber-physical systems, and discover Security vulnerabilities.

This article reviews the traditional application of formal methods, and identifies five unique challenges of formal methods in AI systems, including:

• Develop languages ​​and algorithms about the environment
• Abstract and represent complex ML components and systems
• Propose new canonical formal methods and properties for AI systems and data
• Developed for automated inference Scalable computing engine
• Develop algorithms and technologies designed for trustworthy-by-construction

Based on discussing the latest developments, the author proposes principles to address the above challenges. This article does not just focus on a specific type of AI component such as deep neural networks, or a specific method such as reinforcement learning, but attempts to cover a broader range of AI systems and their design processes. Furthermore, formal methods are only one path toward trustworthy AI, so the ideas in this article are intended to complement methods from other fields. These perspectives are largely informed by thinking about the issues arising from the use of AI in autonomous and semi-autonomous systems, where safety and verification issues are more prominent. Overview

Figure 1 shows a typical process for formal verification, formal synthesis, and formally guided runtime resiliency. The formal verification process starts with three inputs:

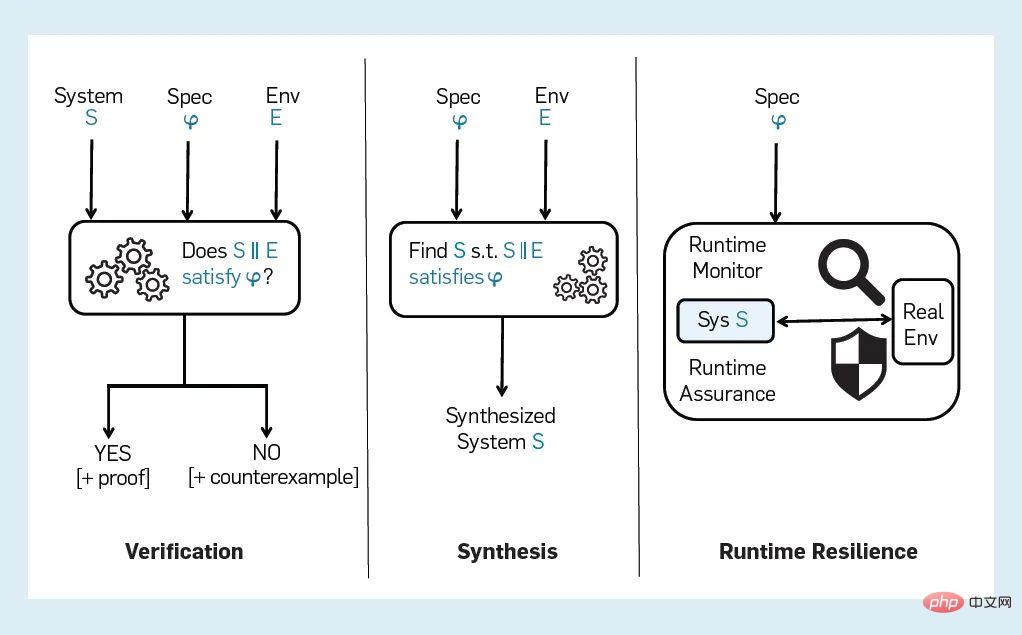
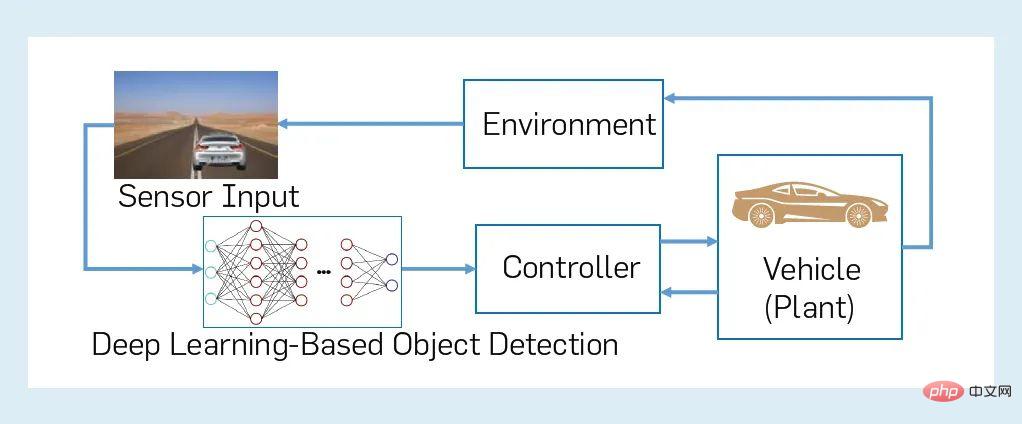
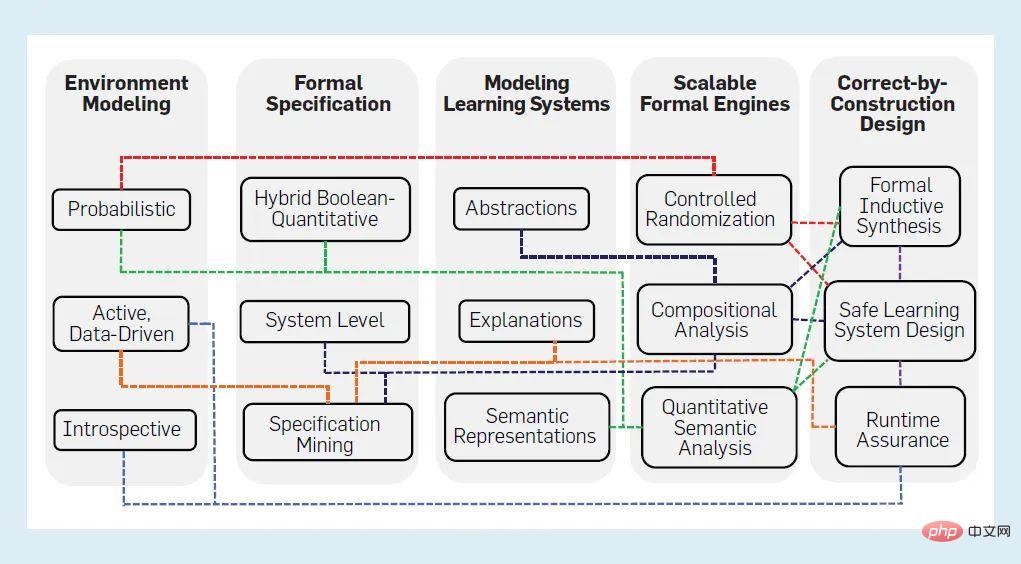
Figure 1: Formal for verification, synthesis, and runtime resiliency Method

1. System model to be verified S
2. Environment model E
3. Attributes to be verifiedΦ

The verifier generates a "yes" or "no" answer as output to indicate S Whether the property Φ in environment E is satisfied. Typically, the "no" output is accompanied by a counterexample, also known as an error trace, which is an execution of the system showing how Φ was forged. Some validation tools also include a proof of correctness or certificate with a "yes" answer. We take a broad perspective on formal methods, including any technique that uses some aspect of formal specification, verification, or synthesis. For example, we include simulation-based hardware verification methods or model-based software testing methods because they also use formal specifications or models to guide the simulation or testing process.

To apply formal verification to an AI system, it must be possible to formally represent at least the three inputs S, E, and Φ. Ideally, there will be Effective decision-making procedures to answer the yes/no questions described previously. However, it is not trivial to construct a good representation even for three inputs, let alone deal with the complexity of the underlying design and verification issues.

#We illustrate the point of this article through an example from the field of semi-autonomous driving. Figure 2 shows an illustrative example of an AI system: a closed-loop CPS that includes a semi-autonomous vehicle with a machine learning component and its environment. Specifically, assume that a semi-autonomous "ego" vehicle has an automated emergency braking system (AEBS) that attempts to detect and classify objects ahead and apply the brakes when needed to avoid a collision. In Figure 2, an AEBS consists of a controller (autonomous braking), a controlled object (controlled vehicle subsystem, including other parts of the autonomy stack) and a sensor (camera), as well as a perception component using DNN . AEBS is combined with the vehicle environment to form a closed-loop CPS. The environment of a "self" vehicle includes agents and objects outside the vehicle (other vehicles, pedestrians, etc.) as well as inside the vehicle (e.g., the driver). The safety requirements of such a closed-loop system can be informally characterized in terms of the property of maintaining a safe distance between the moving "ego" vehicle and any other agent or object on the road. However, there are many nuances in the specification, modeling, and verification of such systems.

Figure 2: Example of closed-loop CPS with machine learning component

First, consider modeling the environment of a semi-autonomous vehicle. Even questions like how many and which agents (both human and non-human) are in the environment, let alone their properties and behaviors, can be subject to considerable uncertainty. Second, perception tasks using AI or ML are difficult, if not impossible, to formalize. Third, components such as DNNs may be complex, high-dimensional objects that operate on complex, high-dimensional input spaces. Therefore, it is very challenging to generate the three inputs S, E, Φ of the formal verification process even in a form that makes the verification tractable.

#If anyone solved this problem, they would be faced with the difficult task of validating an AI-based CPS as complex as Figure 2. In such CPS, a compositional (modular) approach is crucial for scalability, but it can be difficult to implement due to factors such as the difficulty of composition specification. Finally, the correct-by-construction (CBC) approach holds promise for verifiable AI, but it is still in its infancy and heavily dependent on advances in specification and verification. Figure 3 summarizes the five challenging areas of verifiable AI. For each area, we distill current promising approaches into three principles for overcoming challenges, represented as nodes. Edges between nodes show which principles of verifiable AI depend on each other, with common threads of dependency represented by a single color. These challenges and corresponding principles are elaborated below.

Figure 3: Summary of 5 challenge areas of verifiable AI

Environment modeling

Based on AI The environment in which /ML systems run is usually very complex, such as modeling various urban traffic environments in which autonomous vehicles operate. In fact, AI/ML is often introduced into these systems to cope with the complexity and uncertainty of the environment. Current ML design processes often use data to implicitly specify the environment. The goal of many AI systems is to discover and understand their environment as they operate, unlike traditional systems designed for an environment specified a priori. However, all formal verification and synthesis are related to a model of the environment. Therefore, assumptions and properties about the input data must be interpreted into the environment model. We distill this dichotomy into three challenges for modeling the environment of AI systems and develop corresponding principles to address these challenges.

2.1 Modeling Uncertainty​

In the traditional use of formal verification , a commonplace approach is to model the environment as a constrained non-deterministic process, or "disturbance". This “over-approximation” of environmental modeling allows one to capture environmental uncertainty more conservatively without requiring overly detailed models, which would be very inefficient for inference. However, for AI-based autonomy, purely non-deterministic modeling may produce too many spurious error reports, making the verification process useless in practice. For example, in modeling the behavior of surrounding vehicles of an autonomous car, the behaviors of surrounding vehicles are diverse. If pure non-deterministic modeling is adopted, accidents that always occur unexpectedly cannot be taken into account. Additionally, many AI/ML systems implicitly or explicitly make distributional assumptions about data or behavior from the environment, requiring probabilistic modeling. Because it is difficult to determine the underlying distribution accurately, the resulting probabilistic model cannot be assumed to be perfect, and uncertainties in the modeling process must be characterized in the model itself.

#Probabilistic formal modeling. To address this challenge, we propose a form that combines probabilistic and nondeterministic modeling. Probabilistic modeling can be used where a probability distribution can be reliably specified or estimated. In other cases, nondeterministic modeling can be used to overapproximate environmental behavior. While formalisms such as Markov decision processes already provide a way to mix probabilistic and non-deterministic approaches, we believe that richer formalisms such as the probabilistic programming paradigm can provide a more expressive and procedural to model the environment. We predict that in many cases such probabilistic procedures will need to be learned (in part) from data or synthesized. At this point, any uncertainty in the learned parameters must be propagated to the rest of the system and represented in the probabilistic model. For example, convex Markov decision processes provide a way to represent uncertainty in learned transition probability values ​​and extend algorithms for validation and control to account for this uncertainty.

2.2 Unknown variables

In traditional formal verification fields such as verification equipment In the driver, the interface between system S and its environment E is well defined, and E can only interact with S through this interface. For AI-based autonomy, this interface is incomplete and is dictated by sensor and perception components that only partially and noisily capture the environment and cannot capture all interactions between S and E. All variables (characteristics) of the environment are known, let alone perceived. Even in restricted scenarios where environmental variables are known, there is a distinct lack of information about their evolution, especially at the time of design. Additionally, modeling sensors such as lidar that represent environmental interfaces is a significant technical challenge.

Introspective environment modeling. We propose to address this problem by developing introspective design and verification methods, that is, performing introspection in the system S to algorithmically identify assumptions A about the environment E that are sufficient to guarantee that the specification Φ is satisfied. Ideally, A must be the weakest of such assumptions, and must also be efficient enough to generate at design time, monitor at runtime for available sensors and other sources of information about the environment, and facilitate detection when the assumptions are violated. Mitigation measures can be taken. Furthermore, if a human operator is involved, one might hope that A can be translated into an intelligible explanation, that is, S can "explain" to a human why it might not satisfy specification Φ. Handling these multiple requirements, along with the need for good sensor models, makes modeling introspective environments a very important problem. Preliminary work shows that this extraction of monitorable hypotheses is feasible in simple cases, although more work is needed to make it practical.

2.3 Simulating human behavior​

For many AI systems, such as semi-autonomous driving cars , human agents are a critical part of environments and systems. Artificial models of humans fail to adequately capture the variability and uncertainty of human behavior. On the other hand, data-driven approaches for modeling human behavior may be sensitive to the expressiveness and data quality of the features used by the ML model. To achieve high assurance for human AI systems, we must address the limitations of current human modeling techniques and provide assurance on their predictive accuracy and convergence.

#Proactive data-driven modeling. We believe that human modeling requires an active data-driven approach, and that model structure and features represented mathematically are suitable for formal methods. A key part of human modeling is capturing human intent. We propose a three-pronged approach: defining templates or features of the model based on expert knowledge, using offline learning to complete the model for design-time use, and learning and updating the environment model at runtime by monitoring and interacting with the environment . For example, it has been shown that data collected from driving simulators through experiments with human subjects can be used to generate behavioral models of human drivers that can be used to validate and control autonomous vehicles. In addition, adversarial training and attack techniques in computer security can be used for active learning of human models and further designing models for specific human actions that lead to unsafe behavior. These techniques can help develop verification algorithms for human-AI systems.

Formal Specifications

Formal verification relies heavily on formal specifications—precise mathematical statements of what the system should do. Even in areas where formal methods have achieved considerable success, coming up with high-quality formal specifications is a challenge, and AI systems in particular face unique challenges.

3.1 Tasks that are difficult to formalize​

In the AEBS controller in Figure 2 The perception module must detect and classify objects, distinguishing vehicles and pedestrians from other entities. The accuracy of this module requires a formal definition of each type of road user and object, which is extremely difficult in the classic formal method sense. This problem exists in all implementations of this perception module, not just in deep learning-based methods. Similar problems arise with other tasks involving perception and communication, such as natural language processing. So, how do we specify the precision attribute for such a module? What should the specification language be? What tools can we use to build specifications?

End-to-end/system-level specifications. In order to deal with the above challenges, we can change this problem slightly. Rather than directly specifying tasks that are difficult to formalize, we should first focus on precisely specifying the end-to-end behavior of an AI system. From this system-level specification, constraints on the input-output interfaces of components that are difficult to formalize can be obtained. These constraints serve as a component-level specification that is contextually relevant to the overall AI system. For the AEBS example in Figure 2, this involves the specification of the property Φ, which is to maintain a minimum distance from any object during motion, from which we can derive constraints on the DNN input space to capture semantically in adversarial analysis Meaningful input space.

3.2 Quantitative specification vs. Boolean specification​

##Traditionally, formal specifications tend to be of Boolean type, which will give The system behavior is mapped to "true" or "false". However, in AI and ML, specifications are often given as objective functions that regulate costs or rewards. Furthermore, there may be multiple goals, some of which must be met together, while others may require trade-offs against each other in certain circumstances. What is the best way to unify the two normative approaches, Boolean and quantitative? Is there a formalism that uniformly captures common properties of AI components, such as robustness and fairness?

#Mix quantitative and boolean specifications. Both Boolean and quantitative specifications have their advantages: Boolean specifications are easier to compose, but objective functions facilitate validation and synthesis with optimization-based techniques and define finer property satisfaction granularity. One way to bridge this gap is to move to quantitative specification languages, such as using logic with boolean and quantitative semantics (such as metric temporal logic), or combining automata with reward functions for RL. Another approach is to combine Boolean and quantitative specifications into a common specification structure, such as a rulebook, in which specifications can be organized, compared, and summarized in a hierarchical structure. Research has identified several categories of properties of AI systems, including robustness, fairness, privacy, accountability, and transparency. Researchers are proposing new formalisms linking ideas from formal methods and ML to model variations of these properties such as semantic robustness.

3.3 Data vs. Formal Requirements​

The view of “data is specification” Very common in machine learning. Labeled "real" data on a limited set of inputs is often the only specification regarding correct behavior. This is very different from formal methods, which are often given in the form of logic or automata, which define the set of correct behaviors that traverse all possible inputs. The gap between data and norms is noteworthy, especially when the data is limited, biased, or comes from non-experts. We need techniques to formalize the properties of data, both data available at design time and data not yet encountered.

#Specification mining. To bridge the gap between data and formal specifications, we propose using algorithms to infer specifications from data and other observations—so-called specification mining techniques. This type of approach can often be used for ML components, including perception components, because in many cases it does not need to have a precise specification or a human-readable specification. We can also use norm mining methods to infer human intentions and other properties from demonstrations or more complex forms of interactions between multiple agents (human and AI).

Modeling of Learning Systems

In most traditional applications of formal verification, the system S is fixed and known at design time For example, it can be a program or a circuit described in a programming language or a hardware description language. The system modeling problem mainly involves reducing S to a more tractable size by abstracting away irrelevant details. AI systems bring very different challenges to system modeling, mainly due to the use of machine learning:

High-dimensional input space​

#ML components for perception often operate on very high-dimensional input spaces. For example, an input RGB image can be 1000 x 600 pixels, which contains 256 ((1000x600x3)) elements. The input is usually a high-dimensional vector stream like this. Although researchers have used formal methods for high-dimensional input spaces (as in digital circuits), the nature of the input space for ML-based perception is different. It is not entirely Boolean, but is mixed and includes discrete variables. and continuous variables.

High-dimensional parameter/state space​

ML components such as deep neural networks have Thousands to millions of model parameters and primitive components. For example, the state-of-the-art DNN used in Figure 2 has up to 60 million parameters and dozens of layers of components. This creates a huge search space for verification, and the abstraction process needs to be very careful.

Online Adaptation and Evolution​

Some learning systems such as robots using RL will adapt as they encounter new data evolve with new situations. For such systems, design-time verification must account for future evolution of the system's behavior, or be performed incrementally online as the learning system evolves.

Modeling systems in context

For many AI/ML components, Their specification is defined solely by context. For example, to verify the security of the DNN-based system in Figure 2 requires modeling of the environment. We need techniques that model ML components and their context so that semantically meaningful properties can be verified.

#In recent years, many works have focused on improving efficiency to verify the robustness and input-output properties of DNNs. However, this is not enough, we also need to make progress in the following three aspects:

Automatic abstraction and efficient representation​

Automatically generating system abstractions has always been key to formal methods and plays a crucial role in extending the scope of formal methods to large hardware and software systems. To address the challenges of ultra-high-dimensional mixed state spaces and input spaces for ML-based systems, we need to develop efficient techniques for abstracting ML models into simpler models that are more amenable to formal analysis. Some promising directions include: analyzing DNNs using abstract interpretations, developing abstractions for fabricating cyber-physical systems with ML components, and designing new representations (such as star sets) for verification.

Explanation and Cause and Effect

If learners include in their predictions a description of how the predictions derive from the data and context knowledge, we can simplify the task of modeling learning systems. The idea is not new, with terms such as “explanation-based generalization” already being researched by the ML community, but more recently, there is a renewed interest in using logic to explain the output of learning systems. Explanation generation helps debug designs and specifications at design time and helps synthesize robust AI systems that provide assurance at runtime. ML including causal and counterfactual reasoning can also help generate explanations for formal methods.

Semantic feature space

When the generated adversarial input and counterexamples are Adversarial analysis and formal verification of ML models make more sense when the context in which the ML model is used has semantic meaning. For example, techniques that analyze a DNN object detector for small changes in the color of a car or the time of day are more useful than techniques that add noise to a small number of arbitrarily chosen pixels. Currently, most methods fall short at this point. We need semantic adversarial analysis, that is, analyzing ML models in the context of the system they belong to. A key step is to represent the semantic feature space that models the environment in which the ML system operates, rather than the specific feature space that defines the input space for the ML model. This is in line with the intuition that the latent space formed by semantically meaningful parts of the concrete feature space (such as traffic scene images) is much lower than the complete concrete feature space. The semantic feature space in Figure 2 is a low-dimensional space that represents the 3D world around an autonomous vehicle, while the specific feature space is a high-dimensional pixel space. Since the dimensionality of the semantic feature space is lower, it can be searched more easily. However, we also need a "renderer" that maps a point in the semantic feature space to a point in the concrete feature space. Properties of the renderer, such as differentiability, make it easier to apply formal methods to perform goal-oriented searches of the semantic feature space.

Computational engine for design and verification

The effectiveness of formal methods for hardware and software systems is determined by the underlying "computation engine" Driven by advances in - for example, Boolean Satisfiability Solving (SAT), Satisfiability Modular Theory (SMT) and model checking. Given the scale of AI/ML systems, environmental complexity, and novel specifications involved, a new class of computational engines is needed for efficient and scalable training, testing, design, and validation, key challenges that must be overcome to achieve these advances.

5.1 Data set design​

Data is the basic starting point for machine learning. To improve the quality of the ML system, you must improve what it learns. Data quality. How can formal methods help in the systematic selection, design, and enrichment of ML data?

# Data generation for ML has similarities to the problem of test generation for hardware and software. Formal methods have been shown to be effective for systematic, constraint-based test generation, but this is different from the requirements for artificial intelligence systems, where the constraint types can be much more complex - for example, for use of sensors to extract data from complex environments such as traffic conditions) to encode requirements for the “authenticity” of the data captured. Not only do we need to generate data items with specific characteristics (such as tests that find bugs), but we also need to generate collections that satisfy distribution constraints; data generation must meet dataset size and diversity goals for effective training and generalization. These requirements require the development of a new set of formal techniques.

#Controlled randomization in formal methods. There are many aspects to this problem of dataset design. First, the space of "legitimate" inputs must be defined so that the examples are correctly formed according to the application semantics; second, constraints on the similarity measure to real-world data need to be captured; third, there is often a need to generate The distribution of examples is constrained to obtain a guarantee that the learning algorithm converges to the true concept.

We believe these aspects can be addressed by stochastic formal methods - stochastic algorithms for generating data subject to formal constraints and distribution requirements. A new class of technology is promising called controlled improvisation, which generates random strings (example) x that satisfy three constraints:

• A hard constraint that defines the legal x space
• A soft constraint that defines how the generated x must resemble real-world examples
• Define the stochasticity requirements of the output distribution constraints

Currently, the control improvisation theory is still in In its infancy, we are just beginning to understand computational complexity and design efficient algorithms. Improvisation, in turn, relies on recent advances in computational problems such as constrained random sampling, model counting, and generative methods based on probabilistic programming.

5.2 Quantitative verification​

In addition to traditional indicators (state space dimensions, components Quantity, etc.) Beyond measuring the size of an AI system, the types of components can be much more complex. For example, autonomous and semi-autonomous vehicles and their controllers must be modeled as hybrid systems, combining discrete and continuous dynamics; furthermore, the representatives in the environment (humans, other vehicles) may need to be modeled as probabilistic processes. Finally, requirements may involve not only traditional Boolean specifications on safety and liveness, but also quantitative requirements on system robustness and performance, yet most existing verification methods are aimed at answering Boolean verification questions. To address this gap, new scalable engines for quantitative validation must be developed.

#Quantitative semantic analysis. In general, the complexity and heterogeneity of AI systems means that canonical formal verification (Boolean or quantitative) is undecidable—for example, even determining whether a state of a linear hybrid system is reachable is undecidable. . To overcome this obstacle posed by computational complexity, one must use new techniques for probabilistic and quantitative verification on semantic feature spaces to enhance the abstraction and modeling approaches discussed earlier in this section. For canonical formalisms with both Boolean and quantitative semantics, in formalisms such as metric-time logic, formulating verification as optimization is crucial for unifying computational methods from formal methods and computational methods from the optimization literature. For example in simulation-based temporal logic falsification, such falsification techniques can also be used to systematically and adversarially generate training data for ML components, although they must be applied to the semantic feature space for efficiency. Techniques for probabilistic verification should go beyond traditional forms such as Markov chains or MDPs to verify probabilistic programs on semantic feature spaces. Likewise, work on SMT solving must be extended to handle cost constraints more efficiently—in other words, combining SMT solving with optimization methods.

We need to understand what can be guaranteed at design time, how the design process contributes to safe operation at runtime, and how design-time and runtime technologies can effectively Interoperability.

5.3 Combinatorial Reasoning for AI/ML​

For a formal approach that scales to large systems, Combinatorial (Modular) Reasoning is essential. In compositional verification, a large system (e.g., a program) is split into its components (e.g., a program), each component is verified against a specification, and then the component specifications are taken together to produce a system-level specification. A common approach to combinatorial verification is to use assumption-guarantee contracts. For example, a process assumes something about its starting state (preconditions), which in turn guarantees its end state (postconditions). A similar assumption-guarantee paradigm has been used Develop and apply concurrent software and hardware systems.

# However, these paradigms do not cover artificial intelligence systems, in large part due to the fact that artificial intelligence systems are discussed in the "Formal Specifications" section standardization challenges. Composable verification requires compositional specification—that is, the components must be formalizable. However, as described in "Formal Specifications", it may not be possible to formally specify the correct behavior of a perceptual component. Therefore, one of the challenges is to develop combinatorial reasoning techniques that do not rely on having a complete combinatorial specification. Furthermore, the quantitative and probabilistic nature of AI systems requires extending the theory of combinatorial reasoning to quantitative systems and specifications.

#Infer component contracts. The combinatorial design and analysis of AI systems requires progress on multiple fronts. First, there is a need to build on some promising preliminary work to develop a theory for the design and verification of probabilistic guarantees for the semantic space of these systems. Second, new inductive synthesis techniques must be devised to algorithmically generate hypothesis-warranty contracts that reduce normative burden and facilitate combinatorial reasoning. Third, to handle cases such as perception where components do not have precise formal specifications, we propose techniques to infer component-level constraints from system-level analyses, and use such constraints to focus component-level analyses, including adversarial analyses, on search Enter the "relevant" part of the space.

Correcting intelligent systems under construction

In an ideal world, verification would be integrated with the design process, so the system is "under construction amended". For example, verification could be interleaved with the compilation/synthesis steps, assuming a register transfer level (RTL) design flow common in integrated circuits, and perhaps it could be integrated into the synthesis algorithm to ensure that the implementation meets the specification. Can we design a suitable design process for artificial intelligence systems that is gradually revised during construction?

6.1 Specification-driven design of ML components

Given a formal specification, can we design a Demonstrate a machine learning component (model) that satisfies this specification? There are many aspects to the design of this new ML component: (1) designing the data set, (2) synthesizing the structure of the model, (3) generating a representative set of features, (4) synthesizing the hyperparameters and other choices of the ML algorithm aspects, and (5) techniques to automate debugging of ML models or specifications when synthesis fails.

#Formal synthesis of ML components. Solutions are emerging to address some of the problems listed earlier. Properties can be enforced on ML models using semantic loss functions or certified robustness. These techniques can be combined with methods such as neural architecture search to generate correctly constructed models. DNN. Another approach is based on the emerging theory of formal inductive synthesis, that is, synthesis from program instances that satisfy formal specifications. The most common way to solve formal inductive synthesis problems is to use an oracle-guided approach, where a learner is paired with an oracle that answers the query; as in Figure 2 in the example, the oracle can be a forger that generates counterexamples that show how the learning component fails Violation of system-level specifications. Finally, using theorem proving to ensure the correctness of the algorithms used to train ML models is also an important step toward constructing modified ML components.

6.2 System design based on machine learning​

The second challenge is Design a holistic system with learning and non-learning components. Several research questions have arisen: Can we calculate the safe bounds within which ML components can be restricted to operate? Can we design a control or planning algorithm that overcomes the limitations of the ML-aware component it receives as input? Can we devise a combinatorial design theory for artificial intelligence systems? When two ML models are used to sense two different types of sensor data (e.g., LiDAR and visual images), and each model meets its specifications under certain assumptions, under what conditions can the two be used together to Improve overall system reliability?

A prominent example of progress on this challenge is the work on safe learning-based controls. This approach pre-computes a safety envelope and uses learning algorithms to tune the controller within that envelope, requiring techniques to efficiently compute such safety envelopes based on, for example, reachability analysis; similarly, the field of safe RL Significant progress has also been made.

However, these do not fully address the challenges posed by machine learning for perception and prediction—for example, provably safe end-to-end deep reinforcement learning has yet to accomplish.

6.3 Design Time and Runtime for Resilient AI Bridges​

As in “Environment As discussed in the Modeling section, many AI systems operate in environments that cannot be specified a priori, so there will always be environments where correctness cannot be guaranteed. Technologies that implement fault tolerance and error recovery at runtime play an important role in artificial intelligence systems. We need a systematic understanding of what can be guaranteed at design time, how the design process contributes to the safe and correct operation of AI systems at runtime, and how design-time and runtime technologies can interoperate effectively.

#In this regard, the literature on fault-tolerant and reliable systems provides us with the basis for developing runtime assurance techniques—that is, runtime verification and mitigation techniques; e.g. The Simplex approach provides a way to combine complex but error-prone modules with secure, formally verified backup modules. More recently, techniques that combine design-time and runtime assurance approaches have shown that unverified components, including those based on AI and ML, can be wrapped in runtime assurance frameworks to provide guarantees of safe operation. But currently these are limited to specific classes of systems, or they require manual design of runtime monitors and mitigation strategies. There is more to come in approaches such as introspective environment modeling, artificial intelligence-based monitors, and the synthesis of safe fallback strategies. Much work needs to be done.

The design approach to modifying intelligent systems in construction discussed here may introduce overhead that makes it more difficult to meet performance and real-time requirements. But we believe (perhaps non-intuitively) that formal methods can even help improve the performance or energy efficiency of a system in the following sense.

Traditional performance tuning tends to be context-agnostic—for example, tasks need to meet deadlines independently of the environment in which they run. But if these environments are formally characterized at design time, monitored at runtime, and if their system operation is formally verified to be safe, then in such environments ML models can trade accuracy for higher s efficiency. This trade-off may be a fruitful area for future research.

Conclusion

We dissected the problem of designing high-assurance artificial intelligence systems from a formal methods perspective. As shown in Figure 3, we identified five major challenges in applying formal methods to AI systems and developed three design and verification principles for each of the five challenges that have the potential to address this challenge.

The edges in Figure 3 show the dependencies between these principles, such as runtime guarantees relying on introspection and data-driven environment modeling to extract Monitorable assumptions and environmental models. Likewise, to perform system-level analysis, we need to engage in combinatorial reasoning and abstraction, where some AI components may require mining specifications while others generate the correct structure through formal inductive synthesis.

Several researchers, including the authors, have been working on these challenges since 2016, when the original published version of this article introduced some samples progress. We have developed open source tools VerifAI and Scenic that implement techniques based on the principles described in this article and have been applied to industrial-scale systems in autonomous driving and aerospace. These results are just the beginning, and there is much more to be done. Verifiable AI is expected to continue to be a fruitful area of ​​research in the coming years.

The above is the detailed content of Towards Verifiable AI: Five Challenges of Formal Methods. For more information, please follow other related articles on the PHP Chinese website!