Learn Python to solve advanced mathematics problems

Python solves advanced mathematics problems, and my mother no longer has to worry about my learning

---

Use Python to solve limits and derivatives in advanced mathematics , partial derivatives, definite integrals, indefinite integrals, double integrals and other problems

Sympy is a Python scientific computing library, which aims to become a fully functional computer algebra system. SymPy includes functions from basic symbolic arithmetic to calculus, algebra, discrete mathematics and quantum physics. It can display the results in LaTeX.

Sympy official website

Article directory

• Python solves advanced mathematics problems, my mother no longer has to worry about my study
• 1. Practical skills
• • 1.1 Symbolic function
  • 1.2 Expansion expression expand
  • 1.3 Taylor expansion formula series
  • 1.4 Sign expansion
• 2. Find the limit limit
• 3. Find the derivative diff
• • 3.1 Unary function
  • 3.2 Multivariate function
• 4. Integral integrate
• • 4.1 Definite integral
  • 4.2 Indefinite integral
  • 4.3 Double integral
• 5. Solve the system of equations solve
• 6. Calculate the summation

(Free Learning recommendation: python video tutorial）

Watch Looking at this picture, do you feel like you can't breathe? Python is here to help you solve it.

from sympy import *import sympy

Enter the "x= symbols("x")" command to define a symbol

x = Symbol("x")y = Symbol("y")

1. Practical tips

1.1 Symbol function

sympy provides a lot of mathematical symbols, summarized as follows

• Imaginary unit

sympy.I

• Natural logarithm

sympy.E

• Infinity

sympy.oo

• Pi

 sympy.pi

• Find the nth square root

 sympy.root(8,3)

• Get the logarithm

sympy.log(1024,2)

• Find the factorial

sympy.factorial(4)

• Trigonometric function

sympy.sin(sympy.pi)sympy.tan(sympy.pi/4)sympy.cos(sympy.pi/2)

1.2 Expand expression expand

f = (1+x)**3expand(f)

$x^3+3x^2+3x+1$

1.3 泰勒展开公式series

ln(1+x).series(x,0,4)

$x-\frac{x^2}{2}\frac{x^3}{3}O\left(x^4\right)$

sin(x).series(x,0,8)

$x-\frac{x^3}{6}\frac{x^5}{120}-\frac{x^7}{5040}O\left(x^8\right)$

cos(x).series(x,0,9)

$1-\frac{x^2}{2}\frac{x^4}{24}-\frac{x^6}{720}\frac{x^8}{40320}O\left(x^9\right)$

(1/(1+x)).series(x,0,5)

$1-x{x}^2-x^3{x}^{4}O\left(x^5\right)$

tan(x).series(x,0,4)

$x+\frac{x^3}{3}+O\left(x^4\right)$

(1/(1-x)).series(x,0,4)

$1+x+x^2+x^3+O\left(x^4\right)$

(1/(1+x)).series(x,0,4)

$1-x+x^2-x^3+O\left(x^4\right)$

1.4 符号展开

a = Symbol("a")b = Symbol("b")#simplify( )普通的化简simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))#trigsimp( )三角化简trigsimp(sin(x)/cos(x))#powsimp( )指数化简powsimp(x**a*x**b)

$x^{a+b}$

2. 求极限limit

limit(sin(x)/x,x,0)

$1$

f2=(1+x)**(1/x)

f2

${\left(x+1\right)}^{\frac{1}{x}}$

重要极限

f1=sin(x)/x
f2=(1+x)**(1/x)f3=(1+1/x)**x
lim1=limit(f1,x,0)lim2=limit(f2,x,0)lim3=limit(f3,x,oo)print(lim1,lim2,lim3)

1 E E

dir可以表示极限的趋近方向

f4 = (1+exp(1/x))f4

$e^{\frac{1}{x}}+1$

lim4 = limit(f4,x,0,dir="-")lim4

$1$

lim5 = limit(f4,x,0,dir="+")lim5

$\infty$

3. 求导diff

diff(函数,自变量,求导次数)

3.1 一元函数

求导问题

diff(sin(2*x),x)

$2\cos \left(2x\right)$

diff(ln(x),x)

$\frac{1}{x}$

3.2 多元函数

求偏导问题

diff(sin(x*y),x,y)

$-xy\sin \left(xy\right)+\cos \left(xy\right)$

4. 积分integrate

4.1 定积分

• 函数的定积分: integrate(函数，(变量，下限，上限))
• 函数的不定积分: integrate(函数,变量)

f = x**2 + 1integrate(f,(x,-1.1))

$-1.54366666666667$

integrate(exp(x),(x,-oo,0))

$1$

4.2 不定积分

f = 1/(1+x*x)integrate(f,x)

$\mathrm{atan}\left(x\right)$

4.3 双重积分

f = (4/3)*x + 2*y
integrate(f,(x,0,1),(y,-3,4))

$11.6666666666667$

5. 求解方程组solve

#解方程组#定义变量f1=x+y-3f2=x-y+5solve([f1,f2],[x,y])

{x: -1, y: 4}

6. 计算求和式summation

计算求和式可以使用sympy.summation函数，其函数原型为sympy.summation(f, *symbols, **kwargs)

**

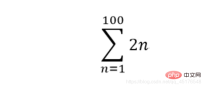
sympy.summation(2 * n,(n,1,100))

10100

到这里就结束了，如果对你有帮助，欢迎点赞关注评论，你的点赞对我很重要。在此也祝愿大家可以把数学学好

相关免费学习推荐：python教程（视频）

The above is the detailed content of Learn Python to solve advanced mathematics problems. For more information, please follow other related articles on the PHP Chinese website!