Home >Web Front-end >JS Tutorial >JavaScript algorithm merge sort algorithm (detailed explanation)
JavaScript algorithm merge sort algorithm (detailed explanation)
- 青灯夜游forward
- 2020-11-09 17:52:184447browse

In this article, we learn the logic behind Merge Sort and implement it in JavaScript. Finally, merge sort is compared with other algorithms in terms of space and time complexity.
The logic behind merge sort
Merge sort uses the concept of divide and conquer to sort a given list of elements. It breaks the problem into smaller sub-problems until they become simple enough to be solved directly.
The following are the steps for merge sort:
1. Divide the given list into two halves (if the number of elements in the list is an odd number, make them roughly equal).
2. Continue dividing the subarrays in the same way until only a single element array remains.
3. Starting from a single element array, merge subarrays in order to sort each merged subarray.
4. Repeat step 3 until you finally get a sorted array.
Taking the array [4, 8, 7, 2, 11, 1, 3] as an example, let us take a look at how merge sort works:
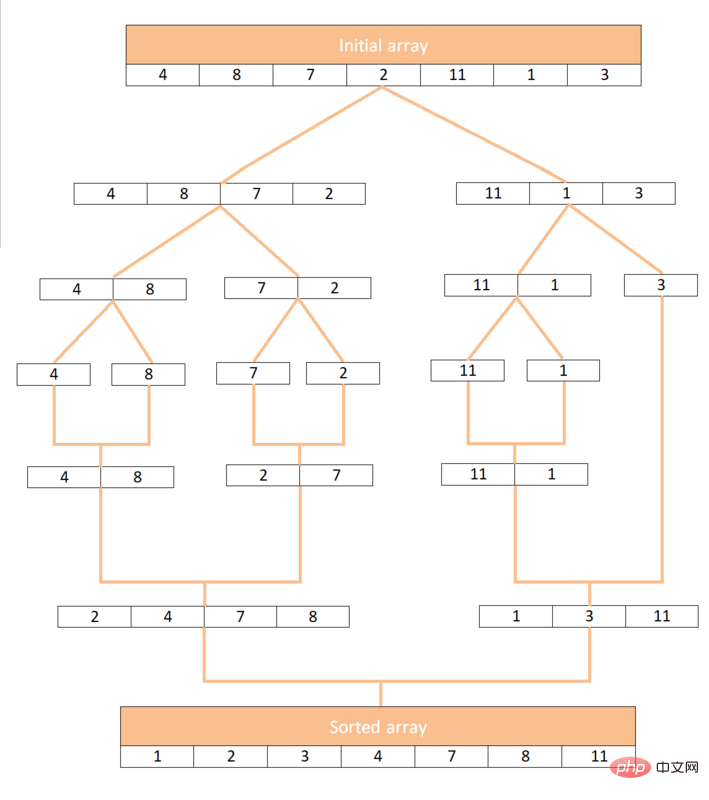
Use JavaScript to implement merge sort
First implement a function that merges two sorted subarrays into one sorted arraymerge(). It is very important to note that the two subarrays are already sorted, and the merge() function is only used for merging them. [Recommended tutorial: "JavaScript Video Tutorial"]
can be achieved by traversing these two sub-arrays:
function merge(left, right) {
let arr = []
// 如果任何一个数组为空,就退出循环
while (left.length && right.length) {
// 从左右子数组的最小元素中选择较小的元素
if (left[0] < right[0]) {
arr.push(left.shift())
} else {
arr.push(right.shift())
}
}
// 连接剩余的元素,防止没有把两个数组遍历完整
return [ ...arr, ...left, ...right ]
}In this function, by arranging the two Merge the ordered subarrays (left, right) to obtain a sorted large array. First, create an empty array. Then take the smaller of the smallest elements in the two sub-arrays left and right and add it to the empty array. We only need to check the first element in the left and right subarrays since they are sorted.
In this process, the selected element is deleted from the subarray (implemented through the shift() function). Continue this process until one of the subarrays becomes empty. Finally, insert the remaining elements of the non-empty subarray (because they have been sorted) into the end of the main array.
Now that we have the code to merge two sorted arrays, here is the final code to implement the merge sort algorithm. This means continuing to split the array until you end up with an array containing only one element:
function mergeSort(array) {
const half = array.length / 2
if(array.length < 2){
return array
}
const left = array.splice(0, half)
return merge(mergeSort(left),mergeSort(array))
}In the code first determine the midpoint and use the splice() function to split the array into two sub-arrays. array. If the number of elements is odd, the number of elements on the left will be one less. Continuously divide the array until an array of single elements is left (array.length ). Then use the <code>merge() function implemented previously to merge the subarrays.
After the code is implemented, test it with the previous use case:
array = [4, 8, 7, 2, 11, 1, 3]; console.log(mergeSort(array));
The output is in line with expectations:
1,2,3,4,7,8,11
Efficiency of merge sort
The worst time of merge sort The complexity is $O(n\\log n)$, which is the same as the optimal time complexity of quick sort. Merge sort is one of the fastest sorting algorithms currently available.
Unlike quick sort, merge sort is not an in-place sorting algorithm, which means it takes up extra space in addition to the input array. This is because we use an auxiliary array to store subarrays. The space complexity of merge sort is $O(n)$.
Another advantage of merge sort is that it is very suitable for multi-threading, because each divided half can be sorted independently. Another common way to reduce the run time of merge sort is to use insertion sort when you reach a relatively small subarray (about 7 elements). This is because insertion sort works very well with small or nearly sorted arrays.
Summary
In this article, we learned about the logic behind the Merge Sort algorithm and implemented it in JavaScript. It is one of the basic sorting algorithms and can help us better understand the divide-and-conquer strategy.
For more programming-related knowledge, please visit: Programming Video Course! !
The above is the detailed content of JavaScript algorithm merge sort algorithm (detailed explanation). For more information, please follow other related articles on the PHP Chinese website!

