How to Deeply Understand Recursion in JavaScript

Recursion in JavaScript refers to the process of a function repeatedly calling itself. The function call is built on the stack. The function call at the top of the stack is always the first to pop up. We can view the stack of calls through the development tools that come with the browser

It is very difficult to truly understand recursion in JavaScript, and some people even call it an unnecessarily memory-intensive and complex version. The "for loop". Next, I will introduce this knowledge to you in detail in the article, I hope it will be helpful to you.

[Recommended course: JavaScript Tutorial]

What is recursion in programming?

Essentially, recursion is when a function or subroutine calls itself repeatedly. All recursive function calls must have a base case. The base case is a specific condition that makes a function return a value rather than calling itself again. To prevent a recursive function from calling itself infinitely, a base case must exist. If omitted or written incorrectly, an error will occur.

An incorrect base case refers to a base case that does not include all possible user inputs, which may result in endless recursive function calls due to specific inputs passed through the base case, resulting in calls to Stack overflow.

Function calls are stored on the call stack

Function calls are stored on the stack, and the call stack is a specific implementation of the stack data structure. It is a LIFO (last in, first out) data structure, which means that function calls placed at the top of the stack are the first to pop.

Example: Calculate the factorial of 5

<script>
 function factorial(num) {
    var nextNum = num - 1;
    if (num === 1) {
        return num; 
    }
    return num * factorial(nextNum);
}
console.log(factorial(5));
</script>

The output result is: 120

In the above code, when parsed to console.log( factorial(5));When,first console.log() will be pushed to the stack, then factorial(5) and its result will be passed to the console.log() function, when we When factorial(5) is entered, the call stack will look like this

Statementreturn num * factorial(nextNum);Indicates that the factorial function returns num (this The example means 5) multiplied by the return value of the recursive function call, of which 4 is passed in. Essentially, the function returns the following value

return 5 * factorial(4);

Because factorial(4) is a function, we will push this function call onto the call stack. Now we will repeat the same process until we reach the base case i. when num equals 1. At this point, the call stack will look like this.

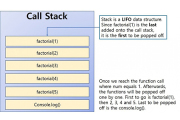
Once we reach the base case, function factorial(1) returns the value 1. So now we know that factorial(1) is equal to 1, factorial(2) ) also returns a non-function value: 2 * factorial(1) , which is 2 * 1 = 2.

Next, factorial(3) returns 3 * factorial(2), which is equal to 6. And so on, until we get factorial(5), which returns 5 * 24 = 120.

How to view the call stack

If you are using the chrome web browser, press f12 (on Windows) to open the chrome developer tools. On the top tab, you will see menu labels like Elements, Profiles, Console, Network, Sources, etc. Click "Source". As shown below

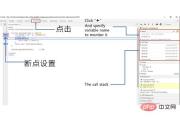
You can visually view the call stack through this development tool. When a recursive function is called with a condition of num === 1, it will return 1. Afterwards, each factorial function call is popped off the stack when the function call returns.

Summary: The above is the entire content of this article, I hope it will be helpful to everyone.

The above is the detailed content of How to Deeply Understand Recursion in JavaScript. For more information, please follow other related articles on the PHP Chinese website!