Home >Backend Development >Python Tutorial >Detailed explanation of Python's use of backtracking subset tree templates to solve maze problems
Detailed explanation of Python's use of backtracking subset tree templates to solve maze problems
- 巴扎黑Original
- 2017-09-02 11:43:462077browse
This article mainly introduces Python's use of backtracking method to solve maze problems. It briefly describes the principles of maze problems and analyzes the relevant operating skills and precautions for solving maze problems in Python based on the backtracking method subset tree template in the form of examples. What is needed Friends can refer to
. This article describes an example of Python using the backtracking method to solve the maze problem. Share it with everyone for your reference, the details are as follows:
Question
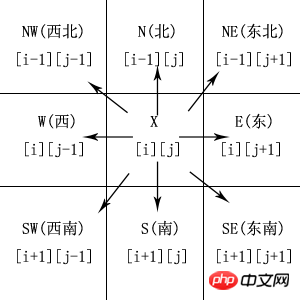
Given a maze, the entrance is known. Ask if there is a path from the entrance to the exit, and if so, output such a path. Note that movement can be performed in eight directions: up, down, left, right, up left, up right, down left, and down right. Entering 0 in the maze means it can be walked, and entering 1 means it is a wall. For convenience, surround the maze with 1 to avoid boundary problems.
Analysis
Considering that left and right are relative, it is modified into eight directions: north, northeast, east, southeast, south, southwest, west, and northwest . In any grid, there are 8 directions to choose from, that is, 8 states to choose from. Therefore, starting from the entrance grid, these 8 states must be traversed every time you enter a grid.
Obviously, the subset tree template of the backtracking method can be applied.
Note that the length of the solution is not fixed.
Code
# 迷宫(1是墙,0是通路)
maze = [[1,1,1,1,1,1,1,1,1,1],
[0,0,1,0,1,1,1,1,0,1],
[1,1,0,1,0,1,1,0,1,1],
[1,0,1,1,1,0,0,1,1,1],
[1,1,1,0,0,1,1,0,1,1],
[1,1,0,1,1,1,1,1,0,1],
[1,0,1,0,0,1,1,1,1,0],
[1,1,1,1,1,0,1,1,1,1]]
m, n = 8, 10 # 8行,10列
entry = (1,0) # 迷宫入口
path = [entry] # 一个解(路径)
paths = [] # 一组解
# 移动的方向(顺时针8个:N, EN, E, ES, S, WS, W, WN)
directions = [(-1,0),(-1,1),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1)]
# 冲突检测
def conflict(nx, ny):
global m,n,maze
# 是否在迷宫中,以及是否可通行
if 0 <= nx < m and 0 <= ny < n and maze[nx][ny]==0:
return False
return True
# 套用子集树模板
def walk(x, y): # 到达(x,y)格子
global entry,m,n,maze,path,paths,directions
if (x,y) != entry and (x % (m-1) ==0 or y % (n-1) == 0): # 出口
#print(path)
paths.append(path[:]) # 直接保存,未做最优化
else:
for d in directions: # 遍历8个方向(亦即8个状态)
nx, ny = x+d[0], y+d[1]
path.append((nx,ny)) # 保存,新坐标入栈
if not conflict(nx, ny): # 剪枝
maze[nx][ny] = 2 # 标记,已访问(奇怪,此两句只能放在if区块内!)
walk(nx, ny)
maze[nx][ny] = 0 # 回溯,恢复
path.pop() # 回溯,出栈
# 解的可视化(根据一个解x,复原迷宫路径,'2'表示通路)
def show(path):
global maze
import pprint, copy
maze2 = copy.deepcopy(maze)
for p in path:
maze2[p[0]][p[1]] = 2 # 通路
pprint.pprint(maze) # 原迷宫
print()
pprint.pprint(maze2) # 带通路的迷宫
# 测试
walk(1,0)
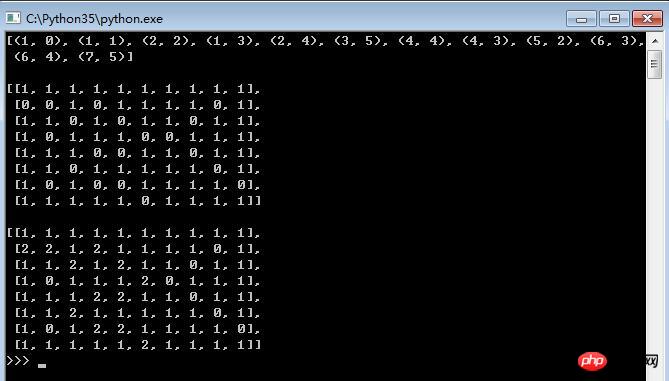
print(paths[-1], '\n') # 看看最后一条路径
show(paths[-1])Rendering
The above is the detailed content of Detailed explanation of Python's use of backtracking subset tree templates to solve maze problems. For more information, please follow other related articles on the PHP Chinese website!

