Solve the 8-queen problem in Python based on the backtracking method subset tree template

This article mainly introduces Python's implementation of the 8-Queens problem based on the backtracking method subset tree template. It briefly explains the principle of the 8-Queens problem and analyzes the specific implementation techniques of Python's backtracking method subset tree template to solve the 8-Queens problem in the form of examples. Friends in need can refer to

This article describes the example of Python's implementation of the 8-queen problem based on the backtracking method subset tree template. Share it with everyone for your reference, the details are as follows:

Problem

Place eight queens on an 8×8 grid chess so that they cannot attack each other, that is No two queens can be in the same row, column or diagonal. How many ways are there to place them?

Analysis

In order to simplify the problem, considering that the 8 queens are in different rows, one queen is placed in each row, and each row The queen can be placed in columns 0, 1, 2, ..., 7. We believe that the queen in each row has 8 states. Then, we only need to apply the subset tree template, starting from row 0, from top to bottom, and traverse the 8 states of the queen in each row.

Code:

##

'''
8皇后问题
'''
n = 8 
x = [] # 一个解（n元数组）
X = [] # 一组解
# 冲突检测：判断 x[k] 是否与前 x[0~k-1] 冲突
def conflict(k):
 global x
 for i in range(k):        # 遍历前 x[0~k-1]
  if x[i]==x[k] or abs(x[i]-x[k])==abs(i-k): # 判断是否与 x[k] 冲突
   return True
 return False
# 套用子集树模板
def queens(k): # 到达第k行
 global n, x, X
 if k >= n:   # 超出最底行
  #print(x)
  X.append(x[:]) # 保存（一个解），注意x[:]
 else:
  for i in range(n): # 遍历第 0~n-1 列（即n个状态）
   x.append(i)  # 皇后置于第i列，入栈
   if not conflict(k): # 剪枝
    queens(k+1)
   x.pop()   # 回溯，出栈
# 解的可视化（根据一个解x，复原棋盘。'X'表示皇后）
def show(x):
 global n
 for i in range(n):
  print('. ' * (x[i]) + 'X ' + '. '*(n-x[i]-1))
# 测试
queens(0) # 从第0行开始
print(X[-1], '\n')
show(X[-1])

Rendering

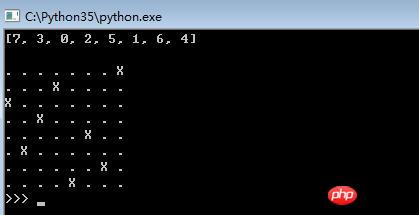
The above is the detailed content of Solve the 8-queen problem in Python based on the backtracking method subset tree template. For more information, please follow other related articles on the PHP Chinese website!