How to implement binary heap in Python

Binary heap is a special kind of heap. Binary heap is a complete binary tree (binary tree) or an approximately complete binary tree (binary tree). There are two types of binary heaps: max-heap and min-heap. Max heap: the key value of the parent node is always greater than or equal to the key value of any child node; min heap: the key value of the parent node is always less than or equal to the key value of any child node.

Binary heap implementation of priority queue

In the previous chapters we learned the data structure of "first in, first out" (FIFO) : Queue (Queue). There is a variant of queue called "Priority Queue" (Priority Queue). The dequeue (Dequeue) operation of the priority queue is the same as that of the queue, and it is dequeued from the head of the queue. But inside the priority queue, the order of elements is determined by "priority": high-priority elements are ranked first in the queue, while low-priority elements are ranked behind. In this way, the priority queue enqueue (Enqueue) operation is more complicated, and the elements need to be queued as far as possible according to the priority. We will find that priority queues are a useful data structure for graph algorithms in the next section.

We naturally think of using sorting algorithms and queue methods to implement priority queues. However, the time complexity of inserting an element into the list is O(n), and the time complexity of sorting the list is O(nlogn). We can use other methods to reduce time complexity. A classic way to implement a priority queue is to use a binary heap (Binary Heap). The binary heap can keep the complexity of entering and dequeuing the priority queue at O(logn).

The interesting thing about the binary heap is that its logical structure is like a binary tree, but it is implemented using non-nested lists. There are two types of binary heaps: the one with the smallest key value always at the head of the queue is called the "minimum heap (min heap)"; conversely, the one with the largest key value always at the head of the queue is called the "maximum heap". Heap (max heap)". In this section we use min-heap.

Operations of Binary Heap

The basic operations of the binary heap are defined as follows:

1. BinaryHeap() : Create an empty binary heap object

2. insert(k): Add new elements to the heap

3. findMin(): Returns the minimum item in the heap, the minimum item remains in the heap

4. delMin(): Returns the smallest item in the heap and deletes it from the heap

5. isEmpty(): Returns whether the heap is empty

6. size(): Returns the number of nodes in the heap

7. buildHeap(list): Creates a new node from a list containing nodes Heap

The code shown below is an example of a binary heap. You can see that no matter which order we add elements to the heap, the smallest element is removed every time. We will implement this process next.

from pythonds.trees.binheap import BinHeap

bh = BinHeap()
bh.insert(5)
bh.insert(7)
bh.insert(3)
bh.insert(11)

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

In order to better implement the heap, we use a binary tree. We must always maintain the "balance" of the binary tree, and we must always keep the operation on the logarithmic scale. A balanced binary tree has the same number of child nodes in the left and right subtrees of the root node. In the implementation of the heap, we use the structure of a "complete binary tree" to approximately achieve "balance". A complete binary tree means that each internal node tree reaches its maximum value, except that the last level can only lack several nodes on the right. Figure 1 shows a complete binary tree.

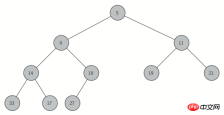
Figure 1: Complete Binary Tree

What’s interesting is that we can achieve a complete tree with a single list. We don't need to use nodes, references or nested lists. Because for a complete binary tree, if the subscript of the node in the list is p, then the subscript of its left child node is 2p and the right node is 2p+1. When we want to find the parent node of any node, we can directly use python's integer division. If the node is indexed n in the list, then the parent node is indexed n//2. Figure 2 shows a complete binary tree and a list representation of the tree. Note the 2p and 2p+1 relationships between parent nodes and child nodes. The list representation of a complete tree combines the properties of a complete binary tree, allowing us to efficiently traverse a complete tree using simple mathematical methods. This also allows us to implement binary heaps efficiently.

The nature of heap order

The way we store elements in the heap depends on the order of the heap. The so-called heap order means that for any node x in the heap, the key value of its parent node p is less than or equal to the key value of x. Figure 2 shows a complete binary tree with heap-ordered properties.

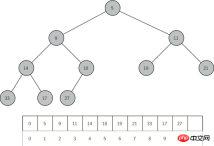
Figure 2: Complete tree and its list representation

Implementation of binary heap operation

接下来我们来构造二叉堆。因为可以采用一个列表保存堆的数据，构造函数只需要初始化一个列表和一个currentSize来表示堆当前的大小。Listing 1 所示的是构造二叉堆的 python 代码。注意到二叉堆的heaplist并没有用到，但为了后面代码可以方便地使用整除，我们仍然保留它。

Listing 1

class BinHeap:
  def init(self):
    self.heapList = [0]
    self.currentSize = 0

我们接下来要实现的是insert方法。首先，为了满足“完全二叉树”的性质，新键值应该添加到列表的末尾。然而新键值简单地添加在列表末尾，显然无法满足堆次序。但我们可以通过比较父节点和新加入的元素的方法来重新满足堆次序。如果新加入的元素比父节点要小，可以与父节点互换位置。图 3 所示的是一系列交换操作来使新加入元素“上浮”到正确的位置。

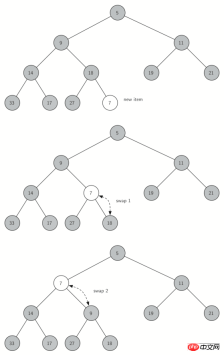
图 3：新节点“上浮”到其正确位置

当我们让一个元素“上浮”时，我们要保证新节点与父节点以及其他兄弟节点之间的堆次序。当然，如果新节点非常小，我们仍然需要将它交换到其他层。事实上，我们需要不断交换，直到到达树的顶端。Listing 2 所示的是“上浮”方法，它把一个新节点“上浮”到其正确位置来满足堆次序。这里很好地体现了我们之前在headlist中没有用到的元素 0 的重要性。这样只需要做简单的整除，将当前节点的下标除以 2，我们就能计算出任何节点的父节点。

在Listing 3 中，我们已经可以写出insert方法的代码。insert里面很大一部分工作是由percUp函数完成的。当树添加新节点时，调用percUp就可以将新节点放到正确的位置上。

Listing 2

def percUp(self,i):
  while i // 2 > 0:
   if self.heapList[i] < self.heapList[i // 2]:
     tmp = self.heapList[i // 2]
     self.heapList[i // 2] = self.heapList[i]
     self.heapList[i] = tmp
   i = i // 2

Listing 3

def insert(self,k):
  self.heapList.append(k)
  self.currentSize = self.currentSize + 1
  self.percUp(self.currentSize)

我们已经写好了insert方法，那再来看看delMin方法。堆次序要求根节点是树中最小的元素，因此很容易找到最小项。比较困难的是移走根节点的元素后如何保持堆结构和堆次序，我们可以分两步走。首先，用最后一个节点来代替根节点。移走最后一个节点保持了堆结构的性质。这么简单的替换，还是会破坏堆次序。那么第二步，将新节点“下沉”来恢复堆次序。图 4 所示的是一系列交换操作来使新节点“下沉”到正确的位置。

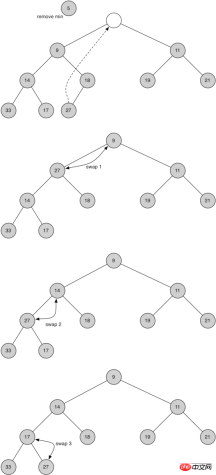
图 4：替换后的根节点下沉

为了保持堆次序，我们需将新的根节点沿着一条路径“下沉”，直到比两个子节点都小。在选择下沉路径时，如果新根节点比子节点大，那么选择较小的子节点与之交换。Listing 4 所示的是新节点下沉所需的percDown和minChild方法的代码。

Listing 4

def percDown(self,i):
  while (i * 2) <= self.currentSize:
    mc = self.minChild(i)
    if self.heapList[i] > self.heapList[mc]:
      tmp = self.heapList[i]
      self.heapList[i] = self.heapList[mc]
      self.heapList[mc] = tmp
    i = mc

def minChild(self,i):
  if i * 2 + 1 > self.currentSize:
    return i * 2
  else:
    if self.heapList[i*2] < self.heapList[i*2+1]:
      return i * 2
    else:
      return i * 2 + 1

Listing 5 所示的是delMin操作的代码。可以看到比较麻烦的地方由一个辅助函数来处理，即percDown。

Listing 5

def delMin(self):
  retval = self.heapList[1]
  self.heapList[1] = self.heapList[self.currentSize]
  self.currentSize = self.currentSize - 1
  self.heapList.pop()
  self.percDown(1)
  return retval

关于二叉堆的最后一部分便是找到从无序列表生成一个“堆”的方法。我们首先想到的是，将无序列表中的每个元素依次插入到堆中。对于一个排好序的列表，我们可以用二分搜索找到合适的位置，然后在下一个位置插入这个键值到堆中，时间复杂度为O(logn)。另外插入一个元素到列表中需要将列表的一些其他元素移动，为新节点腾出位置，时间复杂度为O(n)。因此用insert方法的总开销是O(nlogn)。其实我们能直接将整个列表生成堆，将总开销控制在O(n)。Listing 6 所示的是生成堆的操作。

Listing 6

def buildHeap(self,alist):
  i = len(alist) // 2
  self.currentSize = len(alist)
  self.heapList = [0] + alist[:]
  while (i > 0):
    self.percDown(i)
    i = i - 1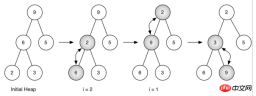

图 5：将列表[ 9, 6, 5, 2, 3]生成一个二叉堆

图 5 所示的是利用buildHeap方法将最开始的树[ 9, 6, 5, 2, 3]中的节点移动到正确的位置时所做的交换操作。尽管我们从树中间开始，然后回溯到根节点，但percDown方法保证了最大子节点总是“下沉”。因为堆是完全二叉树，任何在中间的节点都是叶节点，因此没有子节点。注意，当i=1时，我们从根节点开始下沉，这就需要进行大量的交换操作。可以看到，图 5 最右边的两颗树，首先 9 从根节点的位置移走，移到下一层级之后，percDown进一步检查它此时的子节点，保证它下降到不能再下降为止，即下降到正确的位置。然后进行第二次交换，9 和 3 的交换。由于 9 已经移到了树最底层的层级，便无法进一步交换了。比较一下列表表示法和图 5 所示的树表示法进行的一系列交换还是很有帮助的。

i = 2 [0, 9, 5, 6, 2, 3]
i = 1 [0, 9, 2, 6, 5, 3]
i = 0 [0, 2, 3, 6, 5, 9]

下列所示的代码是完全二叉堆的实现。

def insert(self,k):
   self.heapList.append(k)
   self.currentSize = self.currentSize + 1
   self.percUp(self.currentSize)

  def percDown(self,i):
   while (i * 2) <= self.currentSize:
     mc = self.minChild(i)
     if self.heapList[i] > self.heapList[mc]:
       tmp = self.heapList[i]
       self.heapList[i] = self.heapList[mc]
       self.heapList[mc] = tmp
     i = mc

  def minChild(self,i):
   if i * 2 + 1 > self.currentSize:
     return i * 2
   else:
     if self.heapList[i*2] < self.heapList[i*2+1]:
       return i * 2
     else:
       return i * 2 + 1

  def delMin(self):
   retval = self.heapList[1]
   self.heapList[1] = self.heapList[self.currentSize]
   self.currentSize = self.currentSize - 1

能在O(n)的开销下能生成二叉堆看起来有点不可思议，其证明超出了本书的范围。但是，要理解用O(n)的开销能生成堆的关键是因为logn因子基于树的高度。而对于buildHeap里的许多操作，树的高度比logn要小。

The above is the detailed content of How to implement binary heap in Python. For more information, please follow other related articles on the PHP Chinese website!