Heim >Technologie-Peripheriegeräte >KI >Der Eckpfeiler von AI4Science: Geometrisches graphisches neuronales Netzwerk, die umfassendste Rezension ist hier! Die Renmin University of China Hillhouse hat gemeinsam das Tencent AI Lab, die Tsinghua University, Stanford usw. eröffnet.
Der Eckpfeiler von AI4Science: Geometrisches graphisches neuronales Netzwerk, die umfassendste Rezension ist hier! Die Renmin University of China Hillhouse hat gemeinsam das Tencent AI Lab, die Tsinghua University, Stanford usw. eröffnet.
- 王林nach vorne
- 2024-03-07 21:10:131000Durchsuche

Herausgeber |. XS
Nature veröffentlichte im November 2023 zwei wichtige Forschungsergebnisse: die Proteinsynthesetechnologie Chroma und die Kristallmaterialdesignmethode GNoME. In beiden Studien wurden graphische neuronale Netze als Werkzeug zur Verarbeitung wissenschaftlicher Daten eingesetzt.
Tatsächlich waren graphische neuronale Netze, insbesondere geometrische graphische neuronale Netze, schon immer ein wichtiges Werkzeug für die wissenschaftliche Intelligenzforschung (KI für die Wissenschaft). Dies liegt daran, dass physikalische Systeme wie Partikel, Moleküle, Proteine und Kristalle im wissenschaftlichen Bereich in einer speziellen Datenstruktur – geometrischen Graphen – modelliert werden können.
Im Gegensatz zu allgemeinen topologischen Diagrammen fügen geometrische Diagramme zur besseren Beschreibung des physikalischen Systems unverzichtbare räumliche Informationen hinzu und müssen die physikalische Symmetrie von Translation, Rotation und Spiegelung erfüllen. Angesichts der Überlegenheit geometrischer graphischer neuronaler Netze zur Modellierung physikalischer Systeme sind in den letzten Jahren verschiedene Methoden entstanden, und die Zahl der Veröffentlichungen nimmt weiter zu.
Kürzlich hat sich die Renmin University of China Hillhouse mit dem Tencent AI Lab, der Tsinghua University, Stanford und anderen Institutionen zusammengetan, um ein Übersichtspapier zu veröffentlichen: „A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications“. Basierend auf einer kurzen Einführung in theoretisches Wissen wie Gruppentheorie und Symmetrie überprüft dieser Aufsatz systematisch die relevante Literatur zu geometrischen graphischen neuronalen Netzwerken von Datenstrukturen und Modellen bis hin zu zahlreichen wissenschaftlichen Anwendungen.

Papier-Link:https://arxiv.org/abs/2403.00485
GitHub-Link:https://github.com/RUC-GLAD/GGNN4Science
In dieser Rezension schreibt der Autor Nachher Durch die Recherche von mehr als 300 Referenzen haben wir drei verschiedene Modelle geometrischer neuronaler Graphen zusammengefasst, verwandte Methoden für insgesamt 23 verschiedene Aufgaben zu verschiedenen wissenschaftlichen Daten wie Partikeln, Molekülen und Proteinen eingeführt und mehr als 50 verwandte Datensätze gesammelt. Abschließend blickt die Rezension auf zukünftige Forschungsrichtungen, einschließlich grundlegender geometrischer Graphenmodelle, Kombination mit großen Sprachmodellen usw.
Im Folgenden finden Sie eine kurze Einführung zu jedem Kapitel.
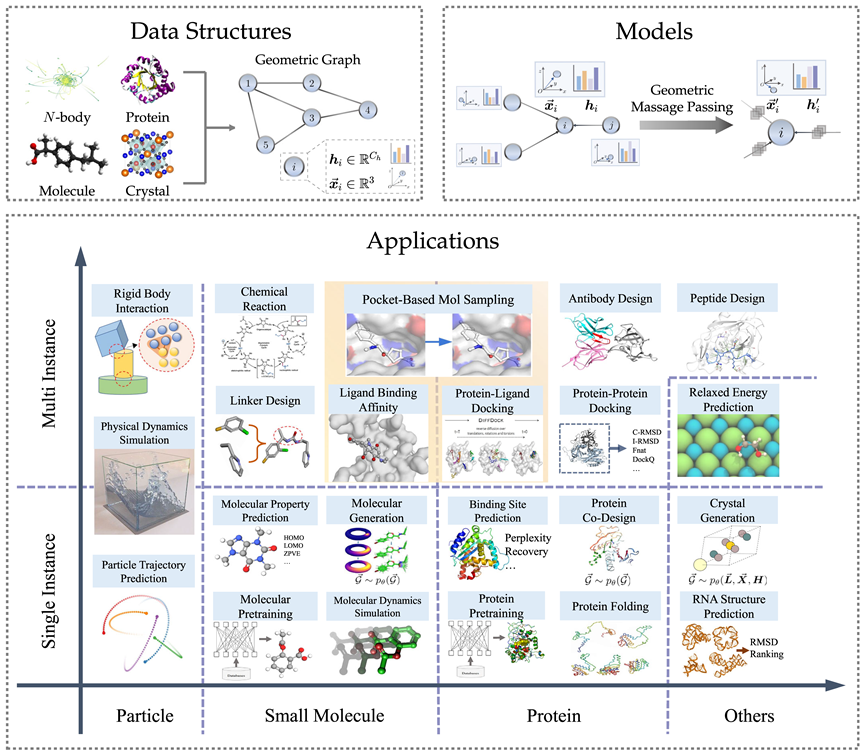
Datenstruktur des geometrischen Diagramms
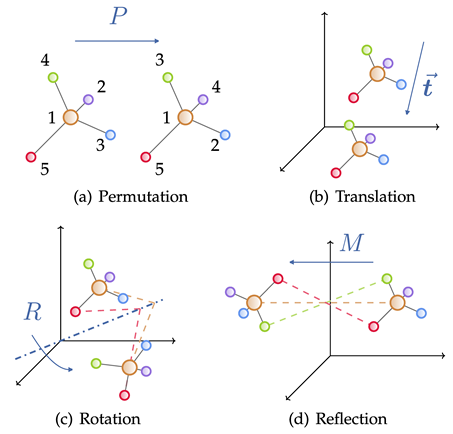
Das geometrische Diagramm besteht aus einer Adjazenzmatrix, Knoteneigenschaften und geometrischen Knoteninformationen (z. B. Koordinaten). Im euklidischen Raum weisen geometrische Figuren normalerweise physikalische Symmetrien der Translation, Rotation und Spiegelung auf. Zur Beschreibung dieser Transformationen werden im Allgemeinen Gruppen verwendet, einschließlich euklidischer Gruppen, Translationsgruppen, orthogonaler Gruppen, Permutationsgruppen usw. Intuitiv kann es als eine Kombination aus vier Vorgängen verstanden werden: Verschiebung, Translation, Rotation und Spiegeln in einer bestimmten Reihenfolge.
Für viele Bereiche der KI für die Wissenschaft sind geometrische Diagramme eine leistungsstarke und vielseitige Darstellungsmethode, mit der viele physikalische Systeme dargestellt werden können, darunter kleine Moleküle, Proteine, Kristalle, physikalische Punktwolken usw.
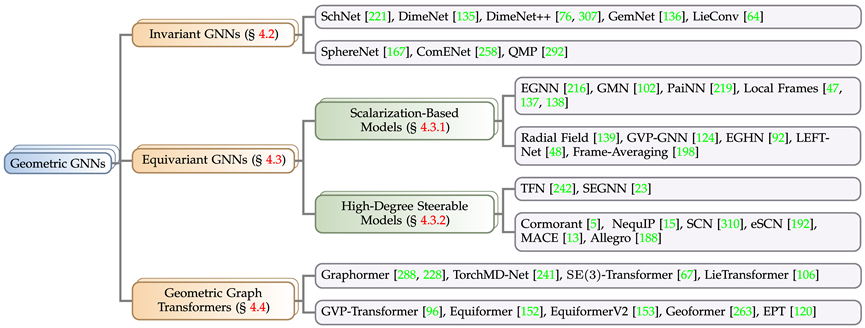
Neuronales Netzwerkmodell mit geometrischem Graphen
Entsprechend den Symmetrieanforderungen der Lösungsziele bei tatsächlichen Problemen unterteilt dieser Artikel neuronale Netzwerke mit geometrischem Graphen in drei Kategorien: invariantes Modell und äquivariantes Modellmodell sowie den geometrischen Graphtransformator Inspiriert durch die Transformer-Architektur ist das äquivariante Modell in ein auf Skalarisierung basierendes Modell und ein hochgradig steuerbares Modell auf Basis sphärischer Harmonisierung unterteilt. Gemäß den oben genannten Regeln sammelt und kategorisiert der Artikel in den letzten Jahren bekannte geometrische Diagramm-Neuronale-Netzwerk-Modelle.
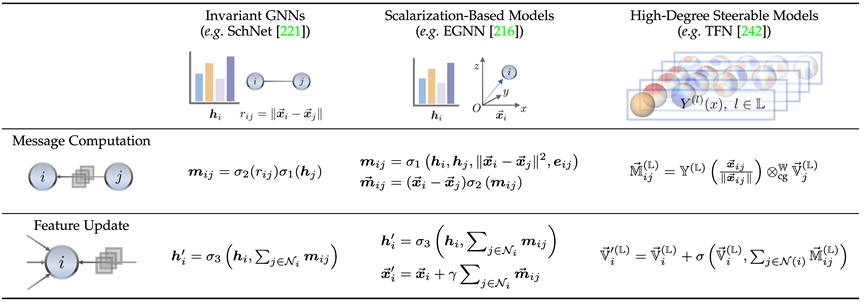
Hier stellen wir anhand der repräsentativen Arbeit kurz die Beziehung zwischen dem invarianten Modell (SchNet[1]), dem Skalarisierungsmethodenmodell (EGNN[2]) und dem steuerbaren Modell höherer Ordnung (TFN[3]) vor von jedem Zweig und Unterschied. Es lässt sich feststellen, dass alle drei Mechanismen zur Nachrichtenübermittlung verwenden, die beiden letztgenannten, bei denen es sich um äquivariante Modelle handelt, jedoch eine zusätzliche geometrische Nachrichtenübermittlung einführen.
Das invariante Modell verwendet hauptsächlich die Eigenschaften des Knotens selbst (wie Atomtyp, Masse, Ladung usw.) und die invarianten Eigenschaften zwischen Atomen (wie Abstand, Winkel [4], Diederwinkel [5]) usw . um Nachrichten zu berechnen.
Darüber hinaus führt die Skalarisierungsmethode zusätzlich geometrische Informationen durch die Koordinatendifferenz zwischen Knoten ein und kombiniert die invarianten Informationen linear als Gewicht der geometrischen Informationen, um die Einführung von Äquivarianz zu erreichen.
Kontrollierbare Modelle höherer Ordnung verwenden sphärische Harmonische und Wigner-D-Matrizen, um die geometrischen Informationen des Systems darzustellen. Diese Methode steuert die Reihenfolge der irreduziblen Darstellung durch den Clebsch-Gordan-Koeffizienten und realisiert so die geometrische Nachrichtenweitergabe Verfahren.
Die Genauigkeit des neuronalen Netzwerks mit geometrischen Graphen wird durch die durch diese Art von Design gewährleistete Symmetrie erheblich verbessert und glänzt auch bei der Generierungsaufgabe.
Die folgende Abbildung zeigt die Ergebnisse der drei Aufgaben der Vorhersage molekularer Eigenschaften, des Protein-Ligand-Dockings und des Antikörperdesigns (Generierung) unter Verwendung des geometrischen graphischen neuronalen Netzwerks und des traditionellen Modells für die drei Datensätze QM9, PDBBind und SabDab It Es ist deutlich zu erkennen, dass geometrische graphische neuronale Netze Vorteile bieten.
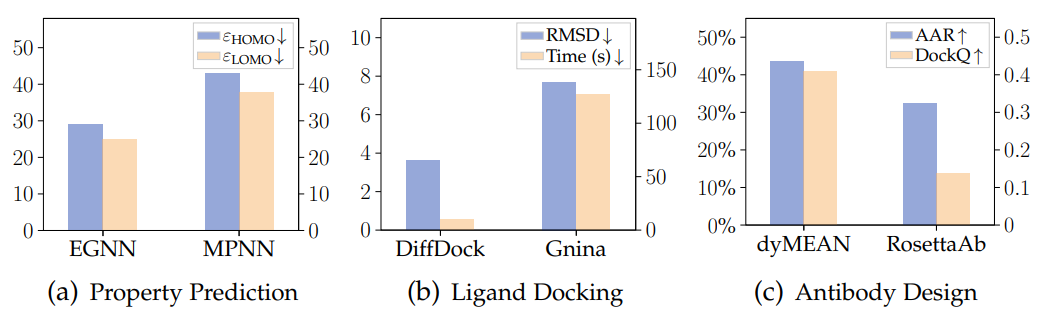
Wissenschaftliche Anwendungen
In Bezug auf wissenschaftliche Anwendungen deckt die Übersicht Physik (Teilchen), Biochemie (kleine Moleküle, Proteine) und andere Anwendungsszenarien wie Kristalle, Aufgabendefinitionen und erforderliche Symmetriegarantien ab den Kategorien ab Es werden die in jeder Aufgabe häufig verwendeten Datensätze und die klassischen Modelldesignideen für diese Art von Aufgaben vorgestellt.
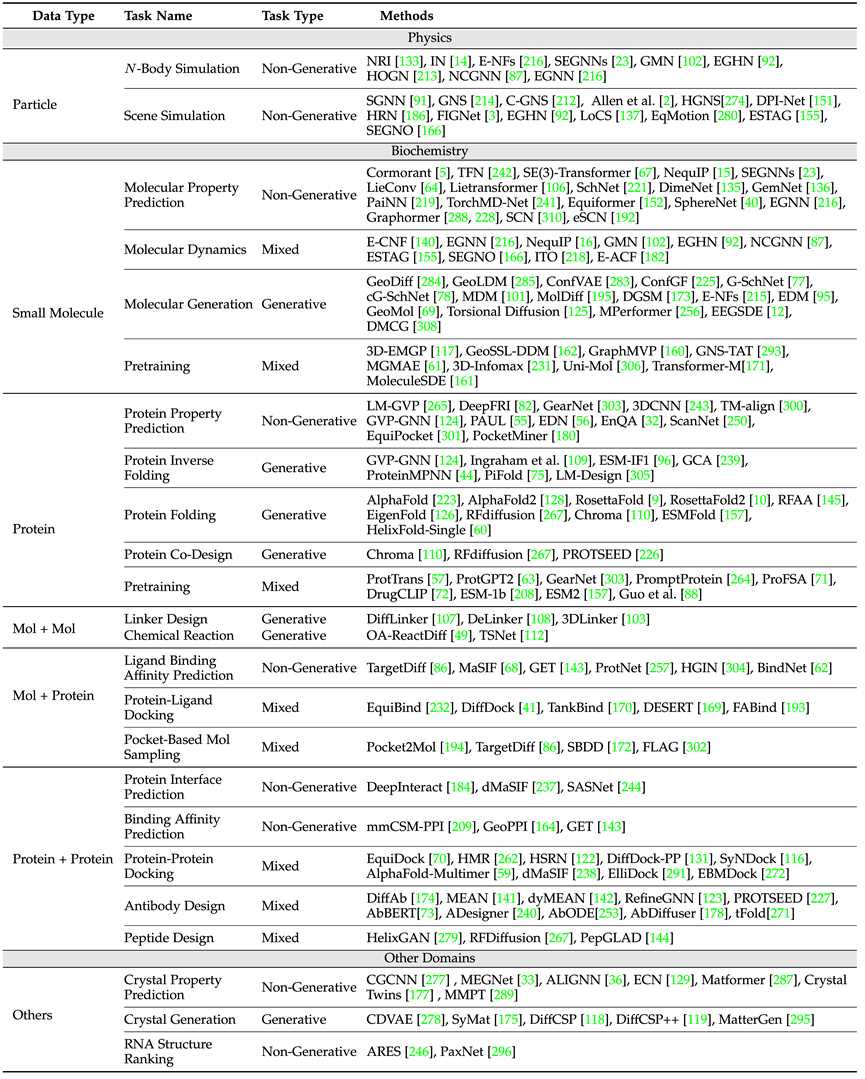
Die obige Tabelle zeigt gängige Aufgaben und klassische Modelle in verschiedenen Bereichen. Darunter unterscheidet der Artikel nach einzelnen Instanzen und mehreren Instanzen (z. B. chemischen Reaktionen, an denen mehrere Moleküle beteiligt sein müssen). kleine Moleküle, kleine Moleküle – Protein, Protein – drei Bereiche des Proteins.
Um das Modelldesign und die Experimententwicklung vor Ort besser zu erleichtern, zählt der Artikel gängige Datensätze und Benchmarks für zwei Arten von Aufgaben basierend auf Einzelinstanzen und mehreren Instanzen und zeichnet die Stichprobengrößen und Aufgabentypen verschiedener Datensätze auf. .
Die folgende Tabelle fasst gängige Einzelinstanz-Aufgabendatensätze zusammen.
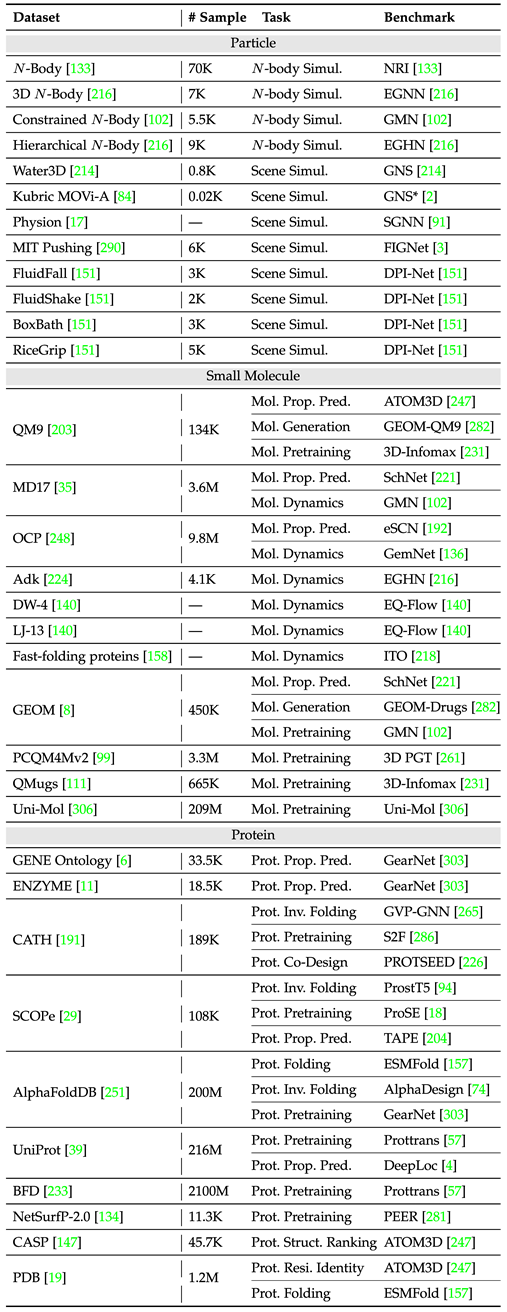
Die folgende Tabelle organisiert gängige Multi-Instanz-Aufgabendatensätze.
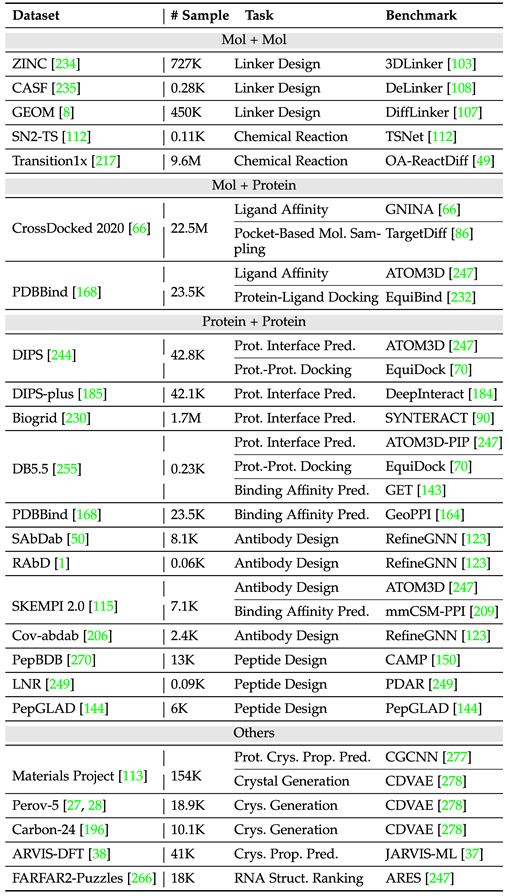
Zukunftsausblick
Der Artikel gibt einen vorläufigen Ausblick auf mehrere Aspekte und hofft, als Ausgangspunkt zu dienen:
1. Das grundlegende geometrische Graphenmodell
ist in verschiedenen Aufgaben und Bereichen vereinheitlicht Die Überlegenheit des Basismodells spiegelt sich voll und ganz in den erheblichen Fortschritten der Modelle der GPT-Serie wider. Wie ein vernünftiger Entwurf im Aufgabenraum, Datenraum und Modellraum durchgeführt werden kann, um diese Idee in den Entwurf eines neuronalen Netzes mit geometrischem Graphen einzuführen, ist immer noch ein interessantes offenes Problem.
2. Effizienter Zyklus aus Modelltraining und experimenteller Verifizierung in der Praxis
Die Erfassung wissenschaftlicher Daten ist teuer und zeitaufwändig, und Modelle, die nur anhand unabhängiger Datensätze bewertet werden, können das Feedback aus der realen Welt nicht direkt widerspiegeln. Die Bedeutung der Erzielung effizienter iterativer experimenteller Paradigmen in der Modellrealität ähnlich wie bei GNoME (das eine End-to-End-Pipeline einschließlich Graphennetzwerktraining, Berechnungen der Dichtefunktionaltheorie und automatisierten Labors für die Materialentdeckung und -synthese integriert) wird von Tag zu Tag zunehmen Tag.
3. Integration mit großen Sprachmodellen (LLMs)
Große Sprachmodelle (LLMs) verfügen nachweislich über umfangreiches Wissen, das verschiedene Bereiche abdeckt. Obwohl es einige Arbeiten gibt, die LLMs für bestimmte Aufgaben wie die Vorhersage molekularer Eigenschaften und das Arzneimitteldesign nutzen, arbeiten sie nur mit Grundelementen oder molekularen Graphen. Es ist immer noch eine große Herausforderung, sie organisch mit geometrischen graphischen neuronalen Netzen zu kombinieren, damit sie 3D-Strukturinformationen verarbeiten und Vorhersagen oder Generierungen für 3D-Strukturen durchführen können.
4. Lockerung der Äquivarianzbeschränkungen
Es besteht kein Zweifel, dass die Äquivarianz entscheidend ist, um die Dateneffizienz und die Fähigkeit zur Modellverallgemeinerung zu verbessern, aber es ist erwähnenswert, dass zu starke Äquivarianzbeschränkungen das Modell manchmal zu sehr einschränken können Leistung. Daher ist es eine sehr interessante Frage, wie Äquivarianz und Anpassungsfähigkeit des entworfenen Modells in Einklang gebracht werden können. Die Erforschung dieses Bereichs kann nicht nur unser Verständnis des Modellverhaltens bereichern, sondern auch den Weg für die Entwicklung robusterer und allgemeinerer Lösungen mit breiterer Anwendbarkeit ebnen.
Referenzen
[1] Schütt K, Kindermans P J, Sauceda Felix H E, et al. Schnet: A Continuous-Filter Convolutional Neural Network for Modeling Quantum Interactions, 2017, 30 .
[2] Satorras V G, Hoogeboom E, Welling M. E (n) äquivariante graphische neuronale Netze[C]//Internationale Konferenz über maschinelles Lernen. PMLR, 2021: 9323-9332.
[3] Thomas N, Smidt T, Kearnes S, et al. Tensorfeldnetzwerke: Rotations- und translatorisch äquivariante neuronale Netzwerke für 3D-Punktwolken[J]. arXiv preprint arXiv:1802.08219, 2018.
[4] Gasteiger J, Groß J, Günnemann S. Directional Message Passing for Molecular Graphs[C]//International Conference on Learning Representations. 2019.
[5] Gasteiger J, Becker F, Günnemann S. Gemnet: Universal Directional Graph Neural Networks for Molecules[J]. Advances in Neural Information Processing Systems, 2021, 34: 6790-6802.
[6] Merchant A, Batzner S, Schoenholz S S, et al. Skalierung von Deep Learning für die Materialentdeckung[J]. Natur, 2023, 624(7990): 80-85.
Das obige ist der detaillierte Inhalt vonDer Eckpfeiler von AI4Science: Geometrisches graphisches neuronales Netzwerk, die umfassendste Rezension ist hier! Die Renmin University of China Hillhouse hat gemeinsam das Tencent AI Lab, die Tsinghua University, Stanford usw. eröffnet.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Lassen Sie uns über die Theorie der Master-Slave-Replikation, Sentry und Clustering in Redis sprechen [ausführliche Erklärung mit Bildern und Text]
- Das Meta-Open-Source-KI-Sprachmodell MusicGen kann Texte und Melodien in vollständige Musik umwandeln
- Das visuelle Talent großer Sprachmodelle: GPT kann auch visuelle Aufgaben durch kontextuelles Lernen lösen

