Heim >Technologie-Peripheriegeräte >KI >Ensemble-Methoden für unbeaufsichtigtes Lernen: Clustering von Ähnlichkeitsmatrizen
Ensemble-Methoden für unbeaufsichtigtes Lernen: Clustering von Ähnlichkeitsmatrizen
- PHPznach vorne
- 2023-11-13 17:53:06769Durchsuche
Beim maschinellen Lernen bezieht sich der Begriff „Ensemble“ auf die parallele Kombination mehrerer Modelle. Die Idee besteht darin, die Weisheit der Masse zu nutzen, um einen besseren Konsens über die endgültige Antwort zu erzielen.

Im Bereich des überwachten Lernens wurde diese Methode umfassend untersucht und angewendet, insbesondere bei Klassifizierungsproblemen mit sehr erfolgreichen Algorithmen wie RandomForest. Oft wird ein Abstimmungs-/Gewichtungssystem eingesetzt, um die Ausgabe jedes einzelnen Modells zu einer robusteren und konsistenteren Endausgabe zu kombinieren.
In der Welt des unbeaufsichtigten Lernens wird diese Aufgabe schwieriger. Da es sich erstens um die Herausforderungen des Fachgebiets selbst handelt, haben wir keine Vorkenntnisse über die Daten, um uns mit irgendeinem Ziel zu vergleichen. Zweitens, weil es immer noch ein Problem ist, eine geeignete Möglichkeit zu finden, Informationen aus allen Modellen zu kombinieren, und es keinen Konsens darüber gibt, wie dies zu bewerkstelligen ist.
In diesem Artikel diskutieren wir den besten Ansatz zu diesem Thema, nämlich die Clusterung von Ähnlichkeitsmatrizen.
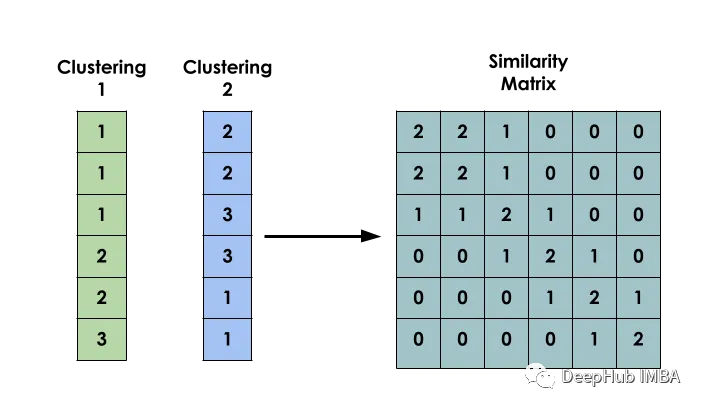
Die Hauptidee dieser Methode ist: Erstellen Sie bei einem gegebenen Datensatz X eine Matrix S, sodass Si die Ähnlichkeit zwischen xi und xj darstellt. Diese Matrix wird basierend auf den Clustering-Ergebnissen mehrerer verschiedener Modelle erstellt.
Binäre Kookkurrenzmatrix
Das Erstellen einer binären Kookkurrenzmatrix zwischen Eingaben ist der erste Schritt beim Erstellen eines Modells

Sie wird verwendet, um anzuzeigen, ob zwei Eingaben i und j zum selben Cluster gehören.
import numpy as np from scipy import sparse def build_binary_matrix( clabels ): data_len = len(clabels) matrix=np.zeros((data_len,data_len))for i in range(data_len):matrix[i,:] = clabels == clabels[i]return matrix labels = np.array( [1,1,1,2,3,3,2,4] ) build_binary_matrix(labels)
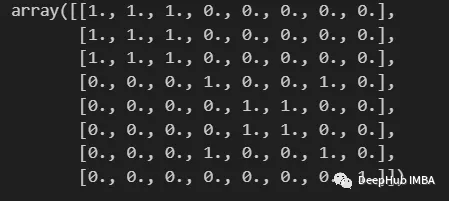
Verwenden Sie KMeans, um eine Ähnlichkeitsmatrix zu erstellen
Wir haben eine Funktion zum Binarisieren unserer Cluster erstellt und können nun mit der Erstellung der Ähnlichkeitsmatrix beginnen.
Wir stellen hier eine gängige Methode vor, bei der nur der Durchschnitt zwischen M Matrizen zum gleichzeitigen Auftreten berechnet wird, die von M verschiedenen Modellen generiert werden. Wir definieren es wie folgt:

Wenn Elemente in denselben Cluster fallen, liegt ihr Ähnlichkeitswert nahe bei 1, und wenn Elemente in verschiedene Gruppen fallen, liegt ihr Ähnlichkeitswert nahe bei 0
Wir werden eine Ähnlichkeit aufbauen Matrix basierend auf den vom K-Means-Modell erstellten Beschriftungen. Durchgeführt unter Verwendung des MNIST-Datensatzes. Der Einfachheit und Effizienz halber werden wir nur 10.000 PCA-reduzierte Bilder verwenden.
from sklearn.datasets import fetch_openml from sklearn.decomposition import PCA from sklearn.cluster import MiniBatchKMeans, KMeans from sklearn.model_selection import train_test_split mnist = fetch_openml('mnist_784') X = mnist.data y = mnist.target X, _, y, _ = train_test_split(X,y, train_size=10000, stratify=y, random_state=42 ) pca = PCA(n_components=0.99) X_pca = pca.fit_transform(X)
Um Vielfalt zwischen den Modellen zu ermöglichen, wird jedes Modell mit einer zufälligen Anzahl von Clustern instanziiert.
NUM_MODELS = 500 MIN_N_CLUSTERS = 2 MAX_N_CLUSTERS = 300 np.random.seed(214) model_sizes = np.random.randint(MIN_N_CLUSTERS, MAX_N_CLUSTERS+1, size=NUM_MODELS) clt_models = [KMeans(n_clusters=i, n_init=4, random_state=214) for i in model_sizes] for i, model in enumerate(clt_models):print( f"Fitting - {i+1}/{NUM_MODELS}" )model.fit(X_pca)
Die folgende Funktion dient zum Erstellen einer Ähnlichkeitsmatrix
def build_similarity_matrix( models_labels ):n_runs, n_data = models_labels.shape[0], models_labels.shape[1] sim_matrix = np.zeros( (n_data, n_data) ) for i in range(n_runs):sim_matrix += build_binary_matrix( models_labels[i,:] ) sim_matrix = sim_matrix/n_runs return sim_matrix
Rufen Sie diese Funktion auf:
models_labels = np.array([ model.labels_ for model in clt_models ]) sim_matrix = build_similarity_matrix(models_labels)
Das Endergebnis ist wie folgt:
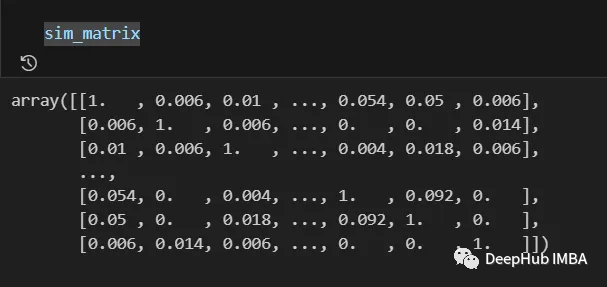
Die Informationen aus der Ähnlichkeitsmatrix können vor dem letzten Schritt noch nachbearbeitet werden , wie z. B. das Anwenden von Logarithmen und Polynomen. Warten Sie auf die Transformation.
In unserem Fall behalten wir die ursprüngliche Bedeutung bei und schreiben sie neu
Pos_sim_matrix = sim_matrix
Clustering der Ähnlichkeitsmatrix
Die Ähnlichkeitsmatrix ist eine Möglichkeit, das durch die Zusammenarbeit aller Clustering-Modelle aufgebaute Wissen darzustellen.
Wir können damit visuell erkennen, welche Einträge mit größerer Wahrscheinlichkeit zum selben Cluster gehören und welche nicht. Allerdings müssen diese Informationen noch in tatsächliche Cluster umgewandelt werden
Dies geschieht durch die Verwendung eines Clustering-Algorithmus, der eine Ähnlichkeitsmatrix als Parameter erhalten kann. Hier verwenden wir SpectralClustering.
from sklearn.cluster import SpectralClustering spec_clt = SpectralClustering(n_clusters=10, affinity='precomputed',n_init=5, random_state=214) final_labels = spec_clt.fit_predict(pos_sim_matrix)
Vergleich mit dem Standardmodell von KMeans
Vergleichen wir es mit KMeans, um zu bestätigen, ob unsere Methode effektiv ist.
Wir werden NMI-, ARI-, Cluster-Reinheits- und Klassenreinheitsindikatoren verwenden, um das Standard-KMeans-Modell zu bewerten und mit unserem Ensemble-Modell zu vergleichen. Darüber hinaus zeichnen wir die Kontingenzmatrix auf, um zu visualisieren, welche Kategorien zu den einzelnen Clustern gehören
from seaborn import heatmap import matplotlib.pyplot as plt def data_contingency_matrix(true_labels, pred_labels): fig, (ax) = plt.subplots(1, 1, figsize=(8,8)) n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels)label_names.sort() contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) heatmap(contingency_matrix.astype(int), ax=ax,annot=True, annot_kws={"fontsize":14}, fmt='d') ax.set_xlabel("Clusters", fontsize=18)ax.set_xticks( [i+0.5 for i in range(n_clusters)] )ax.set_xticklabels([i for i in range(n_clusters)], fontsize=14) ax.set_ylabel("Original classes", fontsize=18)ax.set_yticks( [i+0.5 for i in range(n_classes)] )ax.set_yticklabels(label_names, fontsize=14, va="center") ax.set_title("Contingency Matrix\n", ha='center', fontsize=20)
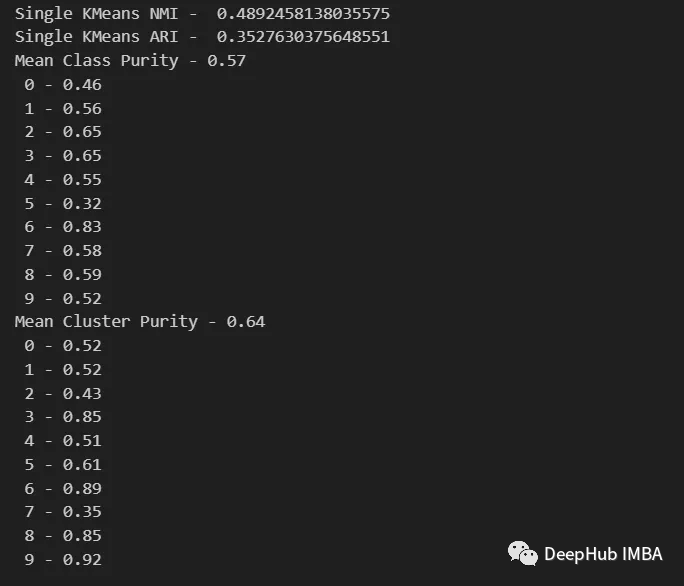
from sklearn.metrics import normalized_mutual_info_score, adjusted_rand_score def purity( true_labels, pred_labels ): n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels) purity_vector = np.zeros( (n_classes) )contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) purity_vector = np.max(contingency_matrix, axis=1)/np.sum(contingency_matrix, axis=1) print( f"Mean Class Purity - {np.mean(purity_vector):.2f}" ) for i, true_label in enumerate(label_names):print( f" {true_label} - {purity_vector[i]:.2f}" ) cluster_purity_vector = np.zeros( (n_clusters) )cluster_purity_vector = np.max(contingency_matrix, axis=0)/np.sum(contingency_matrix, axis=0) print( f"Mean Cluster Purity - {np.mean(cluster_purity_vector):.2f}" ) for i in range(n_clusters):print( f" {i} - {cluster_purity_vector[i]:.2f}" ) kmeans_model = KMeans(10, n_init=50, random_state=214) km_labels = kmeans_model.fit_predict(X_pca) data_contingency_matrix(y, km_labels) print( "Single KMeans NMI - ", normalized_mutual_info_score(y, km_labels) ) print( "Single KMeans ARI - ", adjusted_rand_score(y, km_labels) ) purity(y, km_labels)
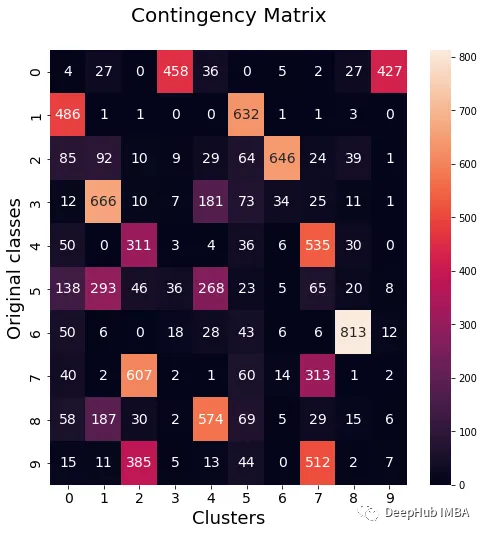
data_contingency_matrix(y, final_labels) print( "Ensamble NMI - ", normalized_mutual_info_score(y, final_labels) ) print( "Ensamble ARI - ", adjusted_rand_score(y, final_labels) ) purity(y, final_labels)
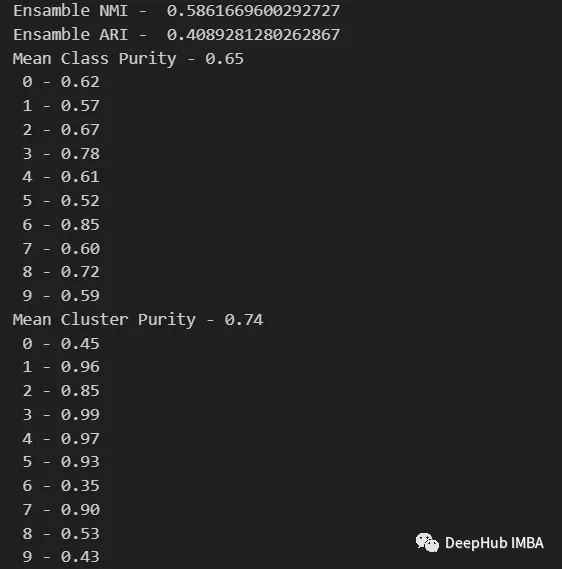
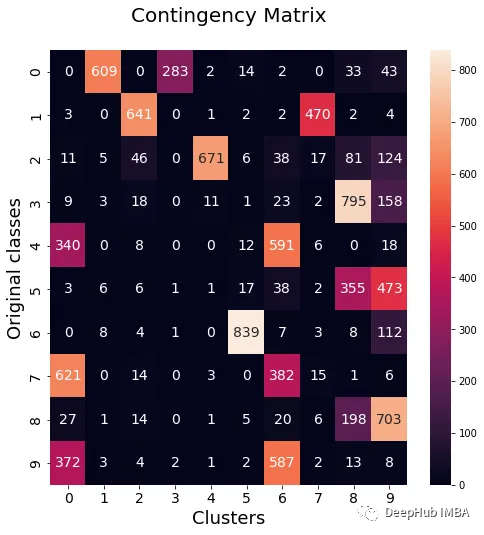
Anhand der oben genannten Werte ist deutlich zu erkennen, dass die Ensemble-Methode die Qualität des Clusterings effektiv verbessern kann. Gleichzeitig ist auch ein konsistenteres Verhalten in der Kontingenzmatrix zu beobachten, mit besseren Verteilungskategorien und weniger „Rauschen“
Das obige ist der detaillierte Inhalt vonEnsemble-Methoden für unbeaufsichtigtes Lernen: Clustering von Ähnlichkeitsmatrizen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

